HMM算法(Hidden Markov Models)揭秘

2024-01-10 15:36:48

序列数据

机器学习的数据通常有两类，最常见的是独立同分布数据，其次就是序列数据。对于前者，一般出现在各种分类/回归问题中，其最大似然估计是所有数据点的概率分布乘积。对于后者，一般出现在各种时间序列问题中，比如在特定时间特定区域内的降雨量数据、每天的货币汇率数据，以及上下文相关的，如语音识别中的声学特征数据、文本的字符序列数据、生物领域如DNA数据等。需要指出，本文介绍的HMM模型适用于一切序列问题，而不仅仅是时序问题。

序列数据的平稳和非平稳性

在平稳状况下，虽然数据随时间变化，但数据的分布(或来源)不变。而对于非平稳状况，情况更为复杂，生成数据的分布本身也在变化。这里我们讨论简单的平稳情况。

马尔科夫模型(Markov models)

与马尔科夫决策过程(MDP)类似，本文讨论的马尔科夫模型也满足马尔科夫性，即未来的预测只依赖于最近的观测，而与过去的历史无关。换言之，马尔科夫性是指不具备记忆特质。这是因为，如果考虑未来观测对所有过去观测的通用依赖，就会导致复杂性的无限增加。而为了预测未来，最近的观测总是比过去历史的观测更有信息量、更有价值。

对于通用的马尔科夫链(Markov chain)，我们可以用以下联合概率表示：

? ? ? ? ? ? ? ? ? ?（公式1）

其中 $x_{1},x_{2},...,x_{N}$ 表示观测序列，该式很好理解，即 $p(x_{1})p(x_{2}|x_{1})p(x_{3}|x_{1}x_{2})...p(x_{N}|x_{1}x_{2}...x_{N-1})=p(x_{1}x_{2}...x_{N-1}x_{N})$

现在考虑一阶马尔科夫链(?rst-order Markov chain)，即满足未来的状态仅与当前状态相关，与任何历史的状态无关，用下图表示：

（图1）

此时上述公式变为：

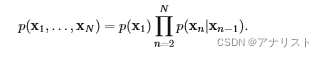? ? ? ?（公式2）

直观表示为： $p(x_{1}x_{2}...x_{N-1}x_{N})=p(x_{1})p(x_{2}|x_{1})p(x_{3}|x_{2})...p(x_{N}|x_{N-1})$

根据马尔科夫性(未来只依赖于最近，而与过去的历史无关)可知：

? ? ? ? ? ?（公式3）

对于平稳序列数据， $p(x_{n}|x_{n-1})$ 条件概率对于不同n是一样的，这样的模型叫做同质马尔科夫链。举个例子，如果这个条件概率依赖于某个可调节的参数(从训练数据中得到)，那么该链的所有条件概率就能共享该参数。

现在考虑高阶马尔科夫链(higher-order Markov chain)，即允许更早的观测对于此刻有影响，比如二阶马尔科夫链(second-order Markov chain)是允许预测值依赖于前两个观测。用下图表示：

（图2）

它的联合概率分布表示为：

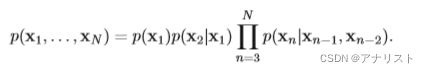? ?（公式4）

高阶马尔科夫链相对于一阶马尔科夫链增加了灵活性，但也增加了参数量。事实上，M阶马尔科夫链的参数随M指数级增加，从而导致该方法不实用。

隐马尔科夫模型(Hidden?Markov models)

HMM在马尔科夫模型中引入隐变量(也叫潜在变量)，已知有 ${x_{1},x_{2},...x_{n}}$ ，现引入 ${z_{1},z_{2},...z_{n}}$ ，具体结构如下图所示：

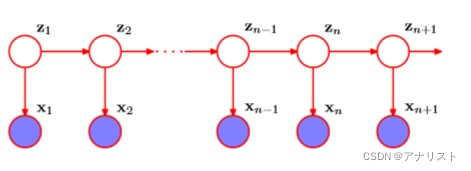（图3）

上图满足当给定 $z_{n}$ 时， $z_{n-1}$ 和 $z_{n+1}$ 是条件独立的，即：

? ? ? ? ? ? ? ? ?（公式5）

因此，HMM的联合概率分布可表示为：

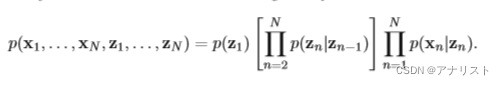? ? ?（公式6）

观察可知，对于任意两个观测值 $x_{n}$ 和 $x_{m}$ ，总存在一条经过隐变量的路径连接它们。因此， $x_{n+1}$ 的预测概率 $p(x_{n+1}|{x_{1},x_{2},...x_{n}})$ 不存在条件独立性，即 $x_{n+1}$ 必定依赖于所有的 ${x_{1},x_{2},...x_{n}}$ ，换言之，观测变量X不满足任意阶的马尔科夫性。

假设每个隐变量 $z_{n}$ 有K个状态(或K个取值)，则它可以表示为K维的向量，其中向量的值为1个元素为1，其余元素全为0. 我们对隐变量 $z_{n}$ 定义一个条件概率 $p(z_{n}|z_{n-1})$ ，那么该概率对于所有n的取值对应了一个矩阵，记为A。这个A就是转移矩阵，其中每个元素叫做转移概率。

我们把A的元素 $A_{jk}$ 定义为 $A_{jk}\equiv p(z_{nk}=1|z_{n-1,j}=1)$ ，它的含义是，在n-1时刻，z在j状态的取值为1，在n时刻，z在k状态的取值为1，事件发生的条件概率（可以看出，和n的取值无关，因为是平稳序列数据）。另外，由于 $A_{jk}$ 是概率，所以满足 $0\leqslant A_{jk}\leqslant 1$ ，以及根据上文状态定义，有 $\sum_{k} A_{jk}=1$ 。

条件概率 $p(z_{n}|z_{n-1})$ 用显式的公式可表示为：

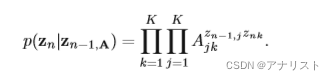? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （公式7）

该式含义是：在以A为转移矩阵的背景下，隐变量Z在n-1时刻(即 $z_{n-1}$ )向n时刻(即 $z_{n}$ )转移的总概率是A矩阵(KxK)若干元素的乘积，具体是n-1时刻在状态j的元素(即 $z_{n-1,j}$ )转移到n时刻在状态k的元素(即 $z_{n,k}$ )。

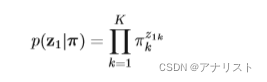
初始隐变量节点 $z_{1}$ 比较特殊，因为它没有父节点(没有节点指向它)。它的边际概率表示为：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式8）

其中 $\pi$ 是概率 $\pi _{k}\equiv p(z_{1k}=1)$ 构成的向量，不难理解， $\pi _{k}$ 的含义是：在时刻1，隐变量Z处于k状态（即初始化状态是k）的概率。由于 $z_{1k}$ 的取值不是0就是1，因此 $\pi _{k}^{z_{1k}}$ 只有在状态取值为k(即 $z_{1k}=1$ )时，才为 $\pi _{k}$ ，而在其余状态(即 $z_{1k}=0$ )都为1.? ?那么 $p(z_{1}|\pi )$ 就表示时刻1的隐变量的边际概率，它可通过对时刻1的所有K个状态累积得到。另外，根据定义有： $\sum_{k} \pi _{k}=1$

对于K=3的状态转移图可用下图表示：

（图4）

图中三个方形表示3个状态。黑色箭头曲线表示状态转移矩阵的元素 $A_{jk}$ 。注意：这不是概率图模型(PGM，即?probabilistic graphical model)，因为每个节点不是单独的变量，而是同一个变量的不同状态(在不同时刻取得)。因此这里的节点用方形而不是圆形表示。

把上图按照时间展开，就得到了一个包含隐变量的网格图，对于HMM就有如下形式：

（图5）

不难发现，每一列对应一个 $z_{n}$ ，每一行代表一个状态。

现在考虑条件概率 $p(x_{n}|z_{n},\phi )$ ，其中 $\phi$ 是决定分布的一系列参数。这个由隐变量决定观测变量的条件概率叫做发射概率(即emission?probabilities)，对于离散的x(包括HMM场景)，一般由条件概率表(CPT，即conditional probability tables?)给出。另外，对于给定的 $\phi$ ，由于 $z_{n}$ 是长度为K的二元向量(元素非0即1)， $p(x_{n}|z_{n},\phi )$ 同样对应一个包含K个元素的向量。

发射概率可具体表示如下：

? ? ? ? ? ? ? ? ? ? ? ? ?（公式9）

一些讨论：对于同质模型，控制隐变量的所有条件概率 $p(z_{n}|z_{n-1})$ 共享转移矩阵A，类似的，发射概率 $p(x_{n}|z_{n})$ 共享所有的 $\phi$ 。另外需要注意到，基于独立同分布数据的混合模型(如GMM)对应本文的特例，其中 $A_{jk}$ 对于所有的j是一样的；因此这导致 $p(z_{n}|z_{n-1})$ 独立于 $z_{n-1}$ 。此时相当于把图3所有的横向箭头曲线去除得到的模型。

现在给出隐变量和观测变量的联合概率分布的具体形式，相当于对公式6的具体化：

? （公式10）

其中 $X=$ { $X_{1},X_{2},...,X_{N}$ }， $Z=$ { $Z_{1},Z_{2},...,Z_{N}$ }， $\theta =$ { $\pi$ , $A$ , $\phi$ }。从上式可看出对A和 $\phi$ 共享的含义。

HMM的极大似然估计(EM算法)

当我们得到观测值 $X=$ { $X_{1},X_{2},...,X_{N}$ }，我们可以利用极大似然估计(MLE)来计算HMM的未知参数。HMM的X的边际概率可表示如下：

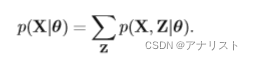? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式11）

$p(X|\theta )$ 是对Z和X的联合概率 $p(X,Z|\theta )$ 对隐变量Z的求和得到。由于联合概率 $p(X,Z|\theta )$ 无法分解为n项因子的乘积，我们无法独立的对每个 $z_{n}$ 进行求和。另外因为有N个变量需要求和，其中每个变量是K维向量(包含K个状态)，因此总共有 $K^{N}$ 项数值需要求和，是HMM链路长度N的指数级别，也就无法直接求和。(注意：公式11的求和对应了图5的网格图中指数量级的路径之和。)

这时候我们想到EM算法。EM算法需要对模型参数进行初始化，记为 $\theta ^{old}$ ；E步骤中，我们利用 $\theta ^{old}$ 计算出隐变量的后验概率 $p(Z|X,\theta ^{old})$ ；然后用该后验概率在M步骤中计算出 $Q(\theta|\theta ^{old} )$ ，具体公式如下：

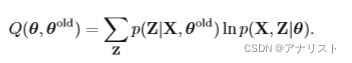? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式12）

（关于EM算法以及公式12的来源，见本人另一篇博客：

EM算法(expectation maximization algorithms)揭秘? ）

现在给出一些函数符号，我们把隐变量 $z_{n}$ 的边际后验概率记为 $\gamma (z_{n})$ ，具体如下：

$\gamma (z_{n})=p(z_{n}|X,\theta^{old} )$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式13）

把两个相邻的隐变量 $z_{n-1}$ 和 $z_{n}$ 的联合后验概率记为 $\xi (z_{n-1},z_{n})$ ，具体如下：

$\xi (z_{n-1},z_{n})=p(z_{n-1},z_{n}|X,\theta^{old} )$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （公式14）

对于每个时刻n，由于 $z_{n}$ 是一个K维的二元向量(只有一个1，其余全是0)，因此 $\gamma (z_{n})$ 是一个K维的非负且元素和为1的向量。类似的， $\xi (z_{n-1},z_{n})$ 是一个KxK维的矩阵，且其元素也是非负且和为1.我们用 $\gamma (z_{nk})$ 表示 $z_{nk}=1$ 的概率。 $\xi (z_{n-1,j},z_{nk})$ 表示 $z_{n-1,j}=1$ 且 $z_{nk}=1$ 的联合概率。由于二元随机变量(非0即1)的期望等于它取值为1的概率，因此有：

? ? ? ? ? ? ? ? ? ? ? ? （公式15）

??? ? ?（公式16）

现在将公式10的联合概率分布代入公式12，并且利用公式15和公式16中 $\gamma$ 和 $\xi$ 的定义，得到：

（公式17）

验证提示：上式右边第一项需要用到 $\pi _{k}$ 的定义 $\pi _{k}\equiv p(z_{1k}=1)$ ， $\pi _{k}$ 的属性 $\sum_{k} \pi _{k}=1$ ，以及 $p(z_{1}|\pi )$ 的定义(即公式8)；上式右边第二项需要用到 $A_{jk}$ 的定义 $A_{jk}\equiv p(z_{nk}=1|z_{n-1,j}=1)$ ，以及 $p(z_{n}|z_{n-1},A)$ 的定义(即公式7)；上式右边第三项需要用到 $p(x_{n}|z_{n},\phi )$ 的定义(即公式9)。

在E步骤中，我们计算 $\gamma (z_{n})$ 和 $\xi (z_{n-1},z_{n})$ 的值，这就需要计算 $\gamma (z)$ 也就是 $\gamma (z)=p(z|X,\theta^{old} )$ 的值，可以看到，和上文提到的EM算法的E步骤对应起来了。

在M步骤中，我们将 $\theta =$ { $\pi ,A,\phi$ }看成变量，同时将 $\gamma (z_{n})$ 和 $\xi (z_{n-1},z_{n})$ 看成常量，对 $Q(\theta|\theta ^{old} )$ 进行最大化。其中对于 $\pi$ 和 $A$ 变量比较简单，可分别用拉格朗日乘子法，得到结果(过程省略)：

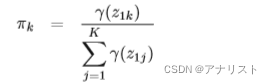? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式18）

? ? ? ? ? ? ? ? ? ? ?（公式19）

EM算法要求对变量 $\pi$ 和 $A$ 选取恰当的初始值，应当分别满足求和为1的约束和非负约束。另外注意到， $\pi$ 和 $A$ 一旦被初始化为0，在EM迭代过程中会一直保持为0.

当把 $\phi _{k}$ 看成变量，对 $Q(\theta|\theta ^{old} )$ 进行最大化时，注意到公式17只有第三项有 $\phi _{k}$ ，此时这一项的形式和高斯混合模型完全一致(见EM应用篇(GMM))。本文的 $\gamma (z_{nk})$ 同样起到某种“责任”的作用，或说负责解释的比例。现在考虑观测概率 $p(x_{n}|\phi _{k})$ 的具体形式，它可以是高斯概率分布，离散多项式概率分布，或伯努利概率分布等。（在李航《统计学习方法》第10章，介绍HMM时，只给出了观测概率矩阵B，并未讨论产生它的概率分布。是否这个讨论是必要的？）

对于高斯概率分布，假设符合以下形式 $p(x|\phi _{k})=N(x|\mu_{k},\Sigma_{k} )$ ，即 $\phi _{k}$ 具体对应了两个参数：高斯的均值 $\mu_{k}$ 和协方差 $\Sigma_{k}$ 。那么此时对 $Q(\theta|\theta ^{old} )$ 最大化，我们得到最优解(过程省略)：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式20）

??? ? ? ? ? ? ? ? ? ? ? ? （公式21）

对于离散多项式概率分布，观测概率 $p(x|z)$ 符合以下形式：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （公式22）

注意，它只有一个参数 $\mu$ 。同样在M步骤中对 $Q(\theta|\theta ^{old} )$ 最大化，得到最优解(过程省略)：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （公式23）

思考：对于伯努利概率分布，情况如何？

EM算法的初始值很重要，这里有个技巧，首先把HMM的时序数据看成独立同分布数据，并用MLE对观测概率分布进行拟合。然后用最终结果来初始化EM算法。

前向与后向算法

下面解决上述EM算法中E步骤的 $\gamma (z_{nk})$ 和 $\xi (z_{n-1,j},z_{nk})$ 的高效计算问题。前向与后向算法(forward-backward algorithm (Rabiner, 1989))就是为了解决这个问题。不过这里有争议：有学者认为前向与后向算法就是Baum-Welch算法(Baum-Welch algorithm (Baum, 1972))，或至少是接近的，或存在包含关系，代表人物是《PRML》的作者。但也有学者认为，前向与后向算法和Baum-Welch算法(属于EM算法)是并列关系，是相互独立的，分别解决HMM的第一个问题(即概率计算问题)和第二个问题(即参数学习问题)，代表人物是《统计学习方法》的作者。而维基百科的观点是：Baum-Welch 算法是EM算法的一个特例，用于查找隐马尔可夫模型(HMM) 的未知参数，它利用前向-后向算法来计算期望步骤(即E步骤)的统计数据。言归正传，前向与后向算法有多个变体，其中最通用的算法叫做alpha-beta算法。

接下来的讨论将忽略对模型参数 $\theta ^{old}$ 的显式依赖，因为它始终是固定的值。以下条件独立性来自论文(Jordan, 2007)：

其中 $X=$ { $X_{1},X_{2},...,X_{N}$ }。这些公式不难证明，有的能直接观察出来，下面依次验证。

公式24：相当于把 $X$ 从n时刻处截断，由两部分的条件独立性得证。

公式25：由于隐变量 $z_{n}$ 能决定观测变量 $x_{n}$ ，因此 $x_{n}$ 作为冗余条件可消去，得证。

公式26：由于隐变量 $z_{n-1}$ 能决定隐变量 $z_{n}$ ，因此 $z_{n}$ 作为冗余条件可消去，得证。

公式27：和公式26不同，这里要决定n+1到N时刻的值，保留 $z_{n+1}$ 即可。

公式28：与公式25类似。

公式29：把 $X$ 从n处分割成三段，结合HMM的图结构，应用贝叶斯公式可得。

公式30： $x_{N+1}$ 只由 $z_{N+1}$ 决定，与 $X$ 无关，得证。

公式31： $z_{N+1}$ 只由 $z_{N}$ 决定，与 $X$ 无关，得证。

现在考虑 $\gamma (z_{nk})$ 的计算问题。我们从 $z_{n}$ 的后验概率 $p(z_{n}|X)$ 入手(见公式13)，其中 $z_{n}$ 是K维二元向量，其每个元素记为 $z_{nk}$ 。利用贝叶斯公式，我们得到：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式32）

与公式13不同，这里省略了 $\theta ^{old}$ 的记号。事实上 $p(X)$ 由 $\theta ^{old}$ 隐式决定，它表示一个似然估计。现在基于公式24的条件独立性，可将 $\gamma (z_{n})$ 进一步改写得到：

? ? ? ? ?（公式33）

其中 $\alpha(z_{n})$ 和 $\beta (z_{n})$ 的定义分别为：

? ? ? ? ? ??

$\alpha(z_{n})$ 表示 $z_{n}$ 和直到n时刻的观测数据的联合概率； $\beta (z_{n})$ 表示所有n+1到N时刻的未来数据相对于 $z_{n}$ 的条件概率。与 $z_{n}$ 一样， $\alpha(z_{n})$ 和 $\beta (z_{n})$ 也是K维向量， $\alpha(z_{n})$ 的每个元素用 $\alpha(z_{nk})$ 表示，此时表示 $z_{nk}=1$ 。 $\beta (z_{nk})$ 同理。

接下来推导 $\alpha(z_{n})$ 的迭代关系，下面的推导用到公式25和公式26的条件独立性，

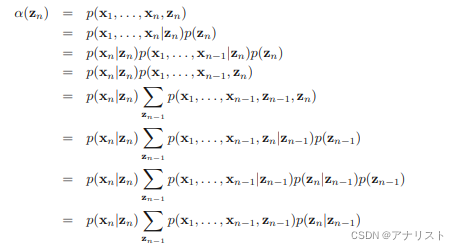
上式最后一步 $p(x_{1},...,x_{n-1},z_{n-1})$ 就是 $\alpha(z_{n-1})$ ，因此我们得到：

? ? ? ? ? ? ? ?（公式36）

上式 $\alpha(z_{n})$ 迭代(即前向算法)的时间复杂度为 $O(K^{2})$ ，它的网格图如下：

（图6）

上图表明 $\alpha(z_{n,1})$ 是由各个 $\alpha(z_{n-1,j})$ 加权求和得到，权重是各个 $A_{j1}$ ，而 $A_{j1}$ 就对应不同状态到达状态k=1的 $p(z_{n}|z_{n-1})$ ，加权求和结果要乘以 $p(x_{n}|z_{n,1})$ 才表示最终的 $\alpha(z_{n,1})$ 。

$\alpha(z_{n})$ 的迭代初始值 $\alpha(z_{1})$ 由以下公式给出：

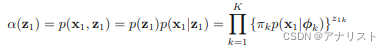? ? ? ? ? （公式37）

这表明每个 $\alpha(z_{1k})$ 以 $\pi _{k}p(x_{1}|\phi_{k} )$ 形式给出，其中k=1,...,K。这样就能顺着隐变量链得到每个 $z_{n}$ 的 $\alpha$ 函数值，即 $\alpha(z_{n})$ 。整个链路有N个时刻，因此总时间复杂度为 $O(K^{2}N)$ 。

类似的，可以推导 $\beta (z_{n})$ 的迭代关系，下面的推导用到公式27和公式28的条件独立性，

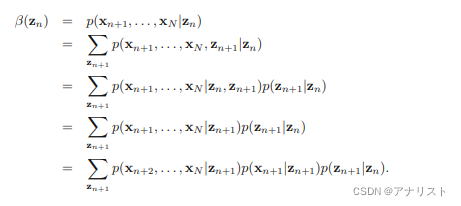
上式最后一步 $p(x_{n+2},...,x_{N}|z_{n+1})$ 就是 $\beta (z_{n+1})$ ，因此我们得到：

? ? ? ? ? ? ?（公式38）

上式 $\beta (z_{n})$ 利用 $\beta (z_{n+1})$ 迭代计算(即后向算法)，同时基于发射概率 $p(x_{n+1}|z_{n+1})$ 以及转移概率 $p(z_{n+1}|z_{n})$ ，它的网格图如下：

（图7）

上图 $A_{1k}$ 对应公式中的 $p(z_{n+1}|z_{n})$ ，表示从n时刻的状态k=1转移到n+1时刻的状态k的转移概率。

为了解决 $\beta (z_{n})$ 的迭代初始化，首先对公式33取n=N，并将公式34代入，可得：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式39）

其中 $X=$ { $X_{1},X_{2},...,X_{N}$ }；而 $\gamma (z_{N})=p(z_{N}|X)$ ，见公式13，省略了 $\theta ^{old}$ 。此时发现，只要规定：对于任意的 $z_{N}$ ，满足 $\beta (z_{N})=1$ ，就能让公式39恒成立（根据贝叶斯公式）。

解决完 $\gamma (z_{nk})$ 的计算问题后，高斯概率分布的M步骤中的 $\mu _{k}$ (即公式20)就有了新的形式：

? ? ? ? ? ?（公式40）

在EM优化过程中，对似然概率 $p(X)$ 的监控很有必要，现在让公式33两边对 $z_{n}$ 求和，那么左边就变为1，即 $\sum_{k}^{}\gamma (z_{nk})=1$ ，那么调整可得：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式41）

当我们取 $\beta (z_{N})=1$ ，即假设 $\beta$ 是所有元素为1构成的向量。那么 $p(X)$ 可简化为：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（公式42）

此时不需要 $\beta$ 的迭代，只需要 $\alpha$ 函数。现在重新理解 $p(X)$ ，原先有 $p(X)=\sum _{Z}p(X,Z)$ ，公式42相当于把 $p(X)$ 计算量从指数级别降低到线性。

接下来解决 $\xi (z_{n-1},z_{n})$ 的计算问题，它的定义来自公式14，即 $p(z_{n-1},z_{n}|X )$ ，结合贝叶斯定理，可得：

??? ?（公式43）

上式比较简单，其中倒数第2行的第一项和第五项相乘等于 $\alpha(z_{n-1})$ ，第三项等于 $\beta (z_{n})$ 。因此我们同样能够利用 $\alpha$ 和 $\beta$ 的迭代，对 $\xi (z_{n-1},z_{n})$ 进行计算。

HMM预测下一个数据

HMM一个有趣且重要的应用是预测下一个x数据。比如已知观察值 $X=$ { $X_{1},X_{2},...,X_{N}$ }，要求预测 $X_{N+1}$ ，这个在实时应用比如金融预测中很重要。我们利用公式29和公式31的条件独立性，结合简单的概率乘法和加法，可得：

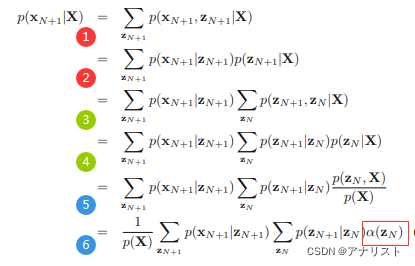（公式44）

第1步将 $x_{N+1}$ 的边际概率扩展为和 $Z_{N+1}$ 的联合概率，需要对 $Z_{N+1}$ 求和消去 $Z_{N+1}$ ；

第2步利用贝叶斯公式，将联合概率分解为两项；

第3步将第2步的边际概率 $p(z_{N+1}|X)$ 扩展为和 $z_{N}$ 的联合概率；

第4步将第3步的联合概率 $p(z_{N+1},z_{N}|X)$ 分解为两项；

第5步利用贝叶斯公式，将 $p(z_{N}|X)$ 改写为 $\frac{p(z_{N},X)}{p(X)}$ ；

第6步将常量 $\frac{1}{p(X)}$ 提取到求和外面，同时套用公式34将 $p(z_{N},X)$ 替换成 $\alpha(z_{N})$

因此 $p(x_{N+1}|X)$ 可通过先前向迭代计算 $\alpha(z_{N})$ ，再分别对 $z_{N}$ 和 $z_{N+1}$ 求和得到。需要指出，对 $z_{N}$ 的求和结果可暂时保存，等到处理 $x_{N+1}$ 时被再次利用。计算 $x_{N+2}$ 等以此类推。

维特比算法(Viterbi algorithm)

HMM的许多应用中，隐变量具有重要的含义，因此有必要找到已知观测序列对应的最有可能的隐状态序列。例如在语音识别中，需要找到给定声音对应的最有可能的文本序列。由于HMM是一个有向图，该问题可以用最大-求和算法(max-sum algorithm或max-product algorithm)精确处理。(说明：最大-求和算法依赖sum-product algorithm，后者将联合概率表达为因子图(factor graph)；最大-求和算法是图模型上的一个DP算法，它用于找到具有最大概率的变量集合。由于篇幅限制，本文不详细介绍这两个算法。)

需要指出，隐变量(或隐状态)的最有可能的序列并不等价于它们单独都是最有可能的。后一个问题可以通过首先运行前向-后向算法来找到每个隐变量的边际概率 $\gamma (z_{nk})$ ，然后单独最大化它得到。但是这样找到的隐状态通常并不是最有可能的状态序列。甚至最差情况，这样找到的状态序列可能具有零概率，即完全不存在，尽管它们单独都是最有可能的，这是因为在转移矩阵中，连接它们的矩阵元素为0。

和最大-求和算法类似，维特比算法也是DP算法，二者时间复杂度接近，都能将指数级别的解码问题转化为线性代价。首先，我们定义 $\omega(z_{n})$ 函数表示到n时刻所有路径中的概率最大值(取对数)为：

$\omega(z_{n})=max_{z_{1},...,z_{n-1}} ln\; p(x_{1},...,x_{n},z_{1},...,z_{n})$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （公式45）

式中把 $z_{1},...z_{n-1}$ 看成自由变量，对每个 $z$ 变量(K维向量)的状态进行选择，选择使得X和Z的联合概率的对数最大化的(即最有可能的序列)，直到到达 $z_{n}$ 。注意：为了简化公式，省略了模型参数 $\theta$ ；事实上，在寻找最有可能序列过程中，参数 $\theta$ 是固定的。

根据HMM的定义(公式6)，结合公式45，不难发现 $\omega(z_{n})$ 的迭代形式：

$\omega(z_{n+1})=ln\; p(x_{n+1}|z_{n+1})+max_{z_{n}} \left \{ ln\; p(z_{n+1}|z_{n}) +\omega(z_{n})\right \}$ ? ?（公式46）

其中初始值 $\omega(z_{1})$ 由公式45可得： $\omega(z_{1})=ln\; p(z_{1})+ln\; p(x_{1}|z_{1})$ ? ? ??（公式47）

一旦完成直到 $z_{N}$ 的最大化，我们将得到最优路径对应的联合概率 $p(X,Z)$ 的ln值。为了找到隐状态的最优序列，我们可以使用一种回溯法(也叫倒推法，back-tracking)。我们把从 $z_{n}$ 到 $z_{n+1}$ 的K个可能状态的概率最大的状态序号保存到 $\psi (k_{n})$ 函数中，其中 $k \in \left \{ 1,...,K \right \}$ 。一旦消息传递到HMM的末端，并且找到了概率最大的 $z_{N}$ 状态，就可以利用该函数进行迭代回溯：

$k_{n}^{max}=\psi (k_{n+1}^{max})$ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??（公式48）

直到推出n=1时刻的最大概率状态序号 $k_{1}^{max}$ ，我们就得到了最优路径：

$k^{max}=(k_{1}^{max},k_{2}^{max},...,k_{N}^{max})$ ? ? ?

参考资料?

?维特比算法，维基百科。

?Baum-Welch 算法，维基百科。

《模式识别与机器学习》，2006 年。

《统计学习方法》，2012年。

文章来源:https://blog.csdn.net/fearlesslpp/article/details/135388734
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！