机器人中的数值优化之罚函数法

2023-12-29 23:51:41

欢迎大家关注我的B站：

偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com)

本文ppt来自深蓝学院《机器人中的数值优化》

目录

1 L2-Penalty Method

1.1等式约束

1.2不等式约束

2 L1-Penalty Method

3 Barrier?Method

1 L2-Penalty Method

1.1等式约束

对于等式约束，罚函数可以惩罚不满足等式约束的点，同时这些点一般不在可行域范围内，因此他也被称为外点罚函数

当罚因子趋向于无穷的时候，点趋向于满足等式约束，此时的最优解就是满足等式约束下的最优解

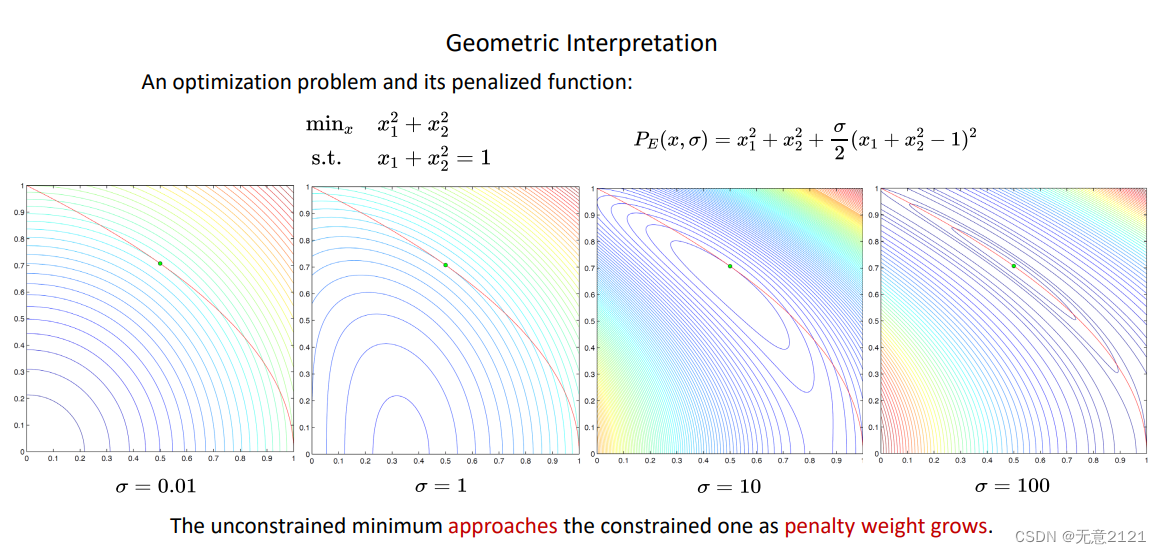
举个例子，可以发现经过加上外点罚函数转换为无约束优化问题

当罚因子变大，最优值越来越接近满足等式约束下的最优值

1.2不等式约束

对于不等式约束，我们只惩罚和c(x)>0的部分，这里就需要一个取大函数，其他和等式约束一样

需要注意的是经过取大函数的处理，目标函数的二阶导不再连续，意味着我们不能利用函数的二阶信息去做优化，而只能用梯度这样的一阶信息去做无约束优化

约束违背量不要求特别小时可采用L2-Penalty Method，如在1e-2~1e-3之间可接受

除了直接一步到位，还可以在迭代过程中逐渐增加罚因子的值

2 L1-Penalty Method

由于L1-罚函数非光滑，因此无约束优化问题P的收敛速度无法保证，这实际上就相当于用牺牲收敛速度的方式来换取优化问题P的精确最优解

3 Barrier?Method

前面介绍的都是处于可行域之外的，称为外点罚函数，自然地，如果需要子问题最优解序列从可行域内部逼近最优解，就需要内点罚函数

内点罚函数也叫障碍函数，因为需要在可行域边界构建一个障碍，防止迭代的时候越过去，其实就是在区域可行域边界的时候，函数值趋于无穷，这样在一个minimize的问题中就不会去接近边界

这里面列举了对数、反函数、指数函数等等

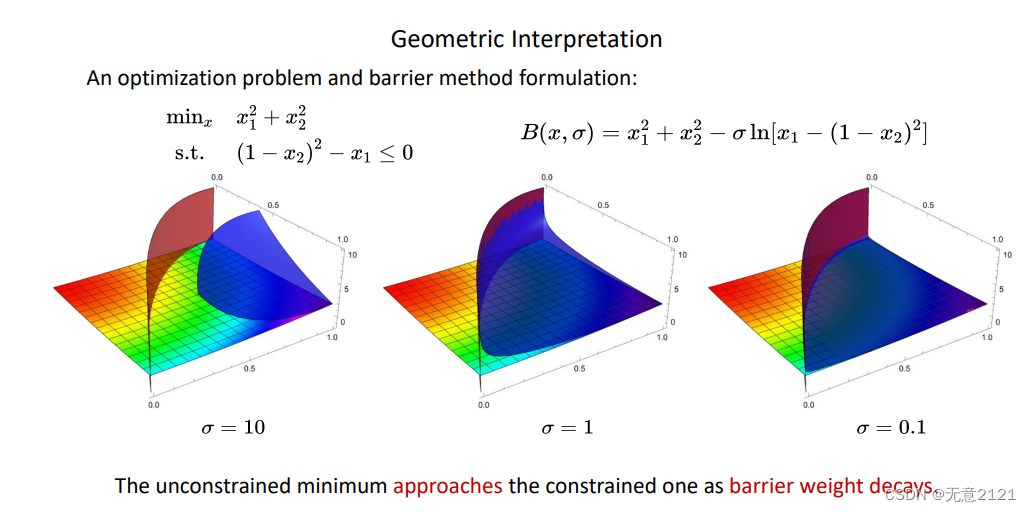
同时当罚因子趋于零的时候最优解才逼近真正的最优解，因为本质上这样构建的障碍数导致变量会远离边界，罚因子趋于零才能减弱障碍罚函数在边界附近的惩罚效果


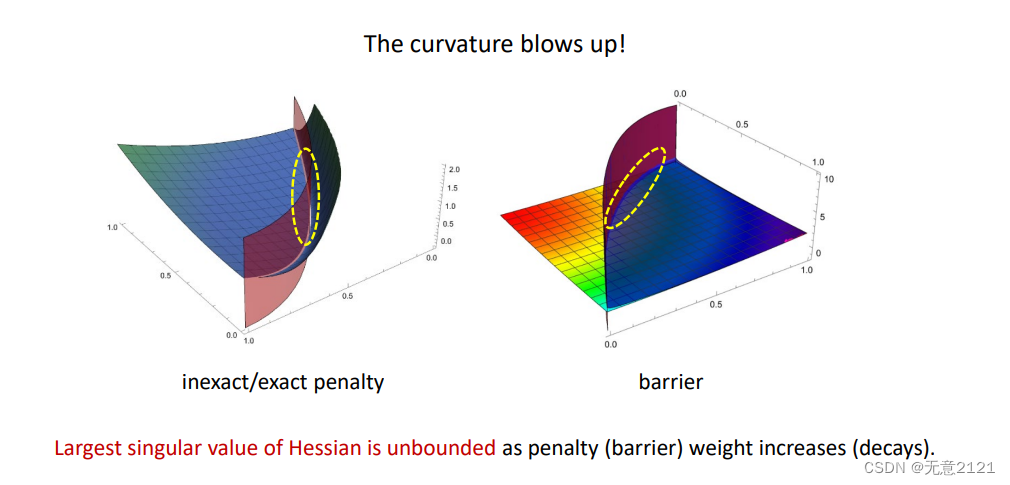
hessian矩阵的条件数很大，奇异值会无界，出现曲率爆炸的问题，但是利用gradient的方法收敛还是很慢

文章来源:https://blog.csdn.net/weixin_65089713/article/details/135297179
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。