[论文学习] BALM: Bundle Adjustment for Lidar Mapping

这篇文档推导起来需要个一整天时间，懵逼一上午，推导一下午。

目录

一. 前言

1） 激光雷达的光束法平差和 图像的光束法平差对比

2）点到线和点到面的距离构建

3）三个贡献

二. 方法

1) 点到线、点到面误差方程构建--->转到特征值上

2) 特征值对点pi的一阶求导

3）appendix A中的公式推导

4）特征值对P点的求导,计算c(m,n)

（1) 特征向量矩阵U对P的求导，

（2) 计算C(m,n)的值

5）计算uk对p的求导

6）得到特征值对点的二阶求导

7）得到点对旋转和平移的求导

8）泰勒二阶展开和求解方程构建

---

一. 前言

1） 激光雷达的光束法平差和 图像的光束法平差对比

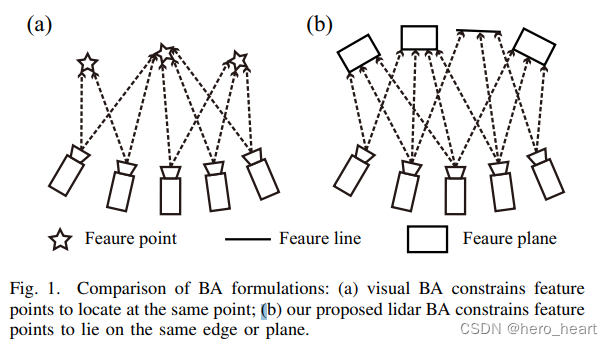
差异是，图像使用投影误差来构建误差方程，优化帧位姿和地图点位置。

激光雷达则是使用点到线和点到面的距离来构建误差方程，只优化当前帧位姿。

2）点到线和点到面的距离构建

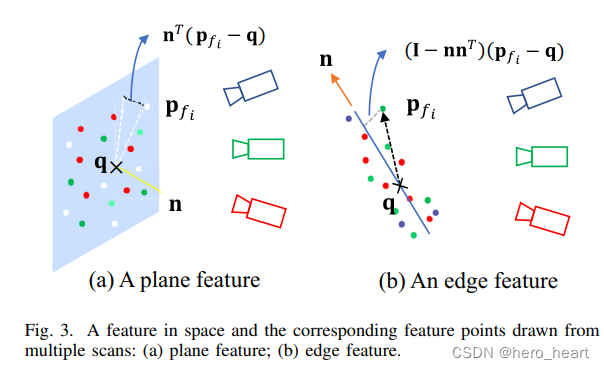
3）三个贡献

? ? (1)相比于图像光束法，激光雷达的光束法只优化位姿，优化参数的维度很小。使快速大尺度稠密特征点优化成为可能。（因为只优化位姿）。

?（2） 为确保高效BA，构建了二阶海森矩阵来求解。

? ? (3) 提出了一个自适应体素搜索来进行高效的特征关联。

?（4） 整合进loam，在固定式激光雷达和旋转激光雷达上做了测试，证明了取得的效果，在一个滑动窗口（20帧）内，做局部的BA，可以达到10HZ.

二. 方法

1) 点到线、点到面误差方程构建--->转到特征值上

把点变换到全局中：

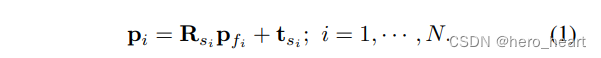
构建的点到面的误差方程：

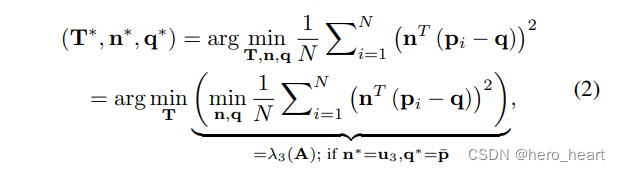
其中认为q的最优值为pi的平均坐标，lamaba3为最小特征值，n的最优值为对应的特征向量，此时n相当于是平面法向。

构建的点到线的误差方程:

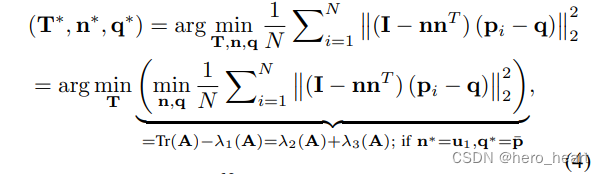
其中认为q的最优值为pi的平均坐标，lamaba1为最大特征值，n的最优值为对应的特征向量，此时n相当于是三维线的方向。Tr(A)为A的三个对角线元素的和，也等于三个特征值的和，因此Tr(A)-lamaba1 = lamaba2+ lamaba3.

从公式3和公式4来看，q点移动并不影响最终的点到面的距离的长度? 和 点到线的距离的长度，因此q的值是不唯一的，但是这不影响优化参数。 因此激光雷达的BA优化方程变成了最小化矩阵A的特征值:

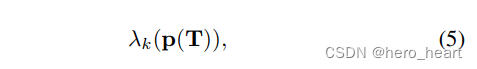
2) 特征值对点pi的一阶求导

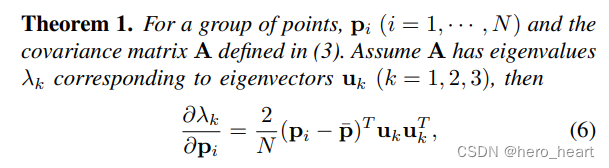
具体推导为：

这个公式不难理解，公式(19）的第一行其实可以展开成(pi-p)*uk*uk*(pi - p拔) + (pj-p)*uk*uk*(pj- p拔)两个相加项分别对pi进行求导就得到公式(19)中中的第3行和第四行，相加后由于所有pi相加就等于p拔，所以相加后就只剩下公式(19)中的最后一行了。这一部分很好理解。这一部分就是一阶导了。

3）appendix A中的公式推导

（1）由于 A* U = LAMABA* U, LAMABA为三个特征值所构建的对角矩阵，所以 UT* A* U =??LAMABA

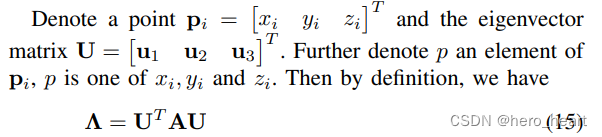
4）特征值对P点的求导,计算c(m,n)

注意后续P点会对旋转和平移求导，这里先对P点进行求导。三个乘数项分别对p进行求导得到：

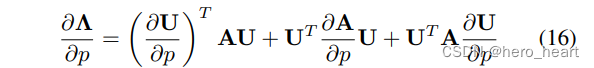
? ? ? ? ? 根据公式（15），可以得到：

?

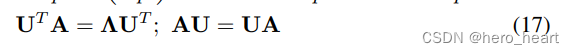所以 公式（16)就变成了:

?

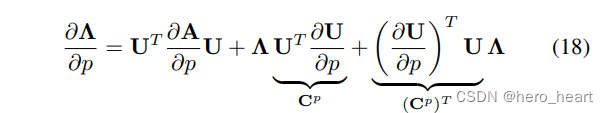
（1) 特征向量矩阵U对P的求导，

U对特征值对应的特征向量所形成的矩阵，因此是一个单位正交矩阵，则：

? ? ?公式两边都对P进行求导得到：

? ? ??

? ? 简写成：

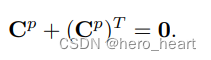
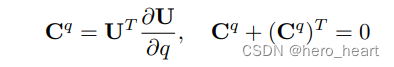
在这里很清楚的要记住一个特点，Cq + CqT = 0 ，则Cq是一个反对称矩阵，则Cq的对角线元素为0。

（4）综合公式(18)和3）中的内容，，可以得到特征值对q的求导为：

? ? ??

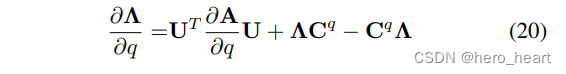
（2) 计算C(m,n)的值

根据公式(20), 特征值对角阵C? 的非对角元素为0， 非对角元素对q的求导也为0，因此下式左边为0，右边改成具体的(m,n)意思是m行n列。um是第m个特征值对应的特征向量，un是第n个特征值对应的特征向量。

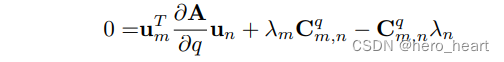
直接移项，因此C(m,n)为：

? ??

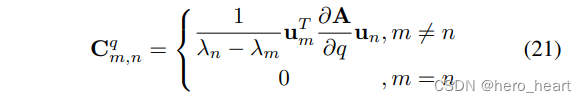
其中 C是反对称矩阵，因此在对角线上是0.

5）计算uk对p的求导

? ? ?uk = U * e? ,在第一个特征值上，e为（1，0，0），在第二个特征值上，e 为（0，1，0）,结合U对q的求导【在3）部分中】，得到公式：

? ? ? ?

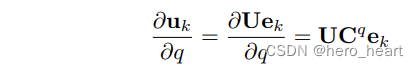
? ? ? ? ? ? ? ?q为pj的x,y,z中的其中一个，因此uk对p的求导为：

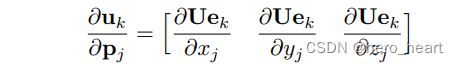
? ? ? ? ? ? ? ? ?进一步的替换为：

? ? ? ? ?

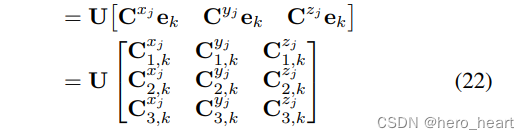
设置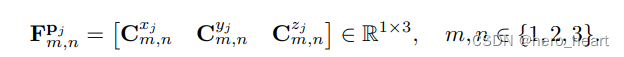

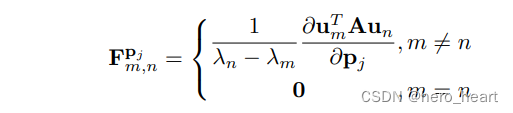
? ? 当m=n的时候C(m,n)为0，因为C是反对称矩阵，对角线元素为0，【看3）中说明】

结合公式(19),?

? ??

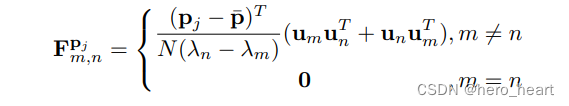
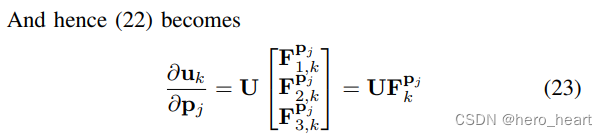
6）得到特征值对点的二阶求导

? ? ? 把公式(19)和公式(23）结合起来，因此二阶导数就出来：

? ? ? ?

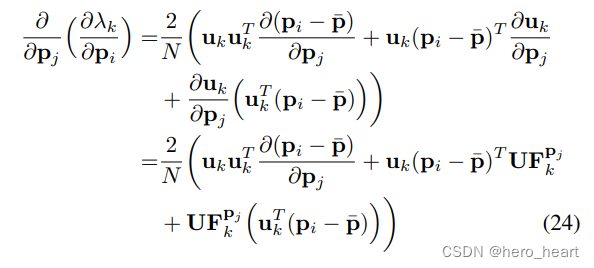
最后作者列了一下这个公式：

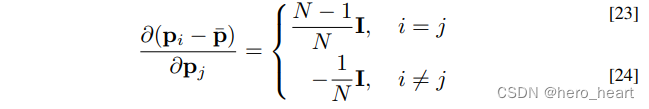
其实这个公式不仅用于公式（24），还用于公式（19）的推导。

7）得到点对旋转和平移的求导

这样根据链式求导原理，就可以得到特征值对旋转和平移的求导了。也可以得到二阶和一阶的特征值对旋转和平移的求导了。

8）泰勒二阶展开和求解方程构建

p 是位姿。

J 和H 简化表达为：

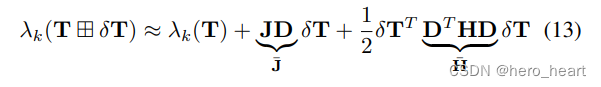
对泰勒展开进行求导，用一阶和二阶系数计算结果

至此整个推导完毕。