图神经网络｜10.4 GCN 变换原理的解读

2024-01-08 06:05:25

由9.3-邻接矩阵的变换可知，理解矩阵通过两个度矩阵的逆进行归一化。
微观上看， a i j a_{ij} aij?这个元素将会乘上 1 d e g ( v i ) d e g ( v j ) \frac{1}{\sqrt{deg_(v_i)\sqrt{deg(v_j)}}} deg(?vi?)deg(vj?) ? ?1?
其现实意义如下——
在这里插入图片描述
比如预测人脉图中某一个人是否为富二代。
假设节点j是一个富二代，且从i和j这对关系进行考虑，j可能认识很多人（对应的度很大），而j可能并不是很认真去对待节点i，所以i和j这对关系对i是一个富二代身份的贡献量应该与j的度数呈反比。
（如果j是一个富二代，又没有几个朋友，几乎只和i认识，那么大概率i也是一个富二代）
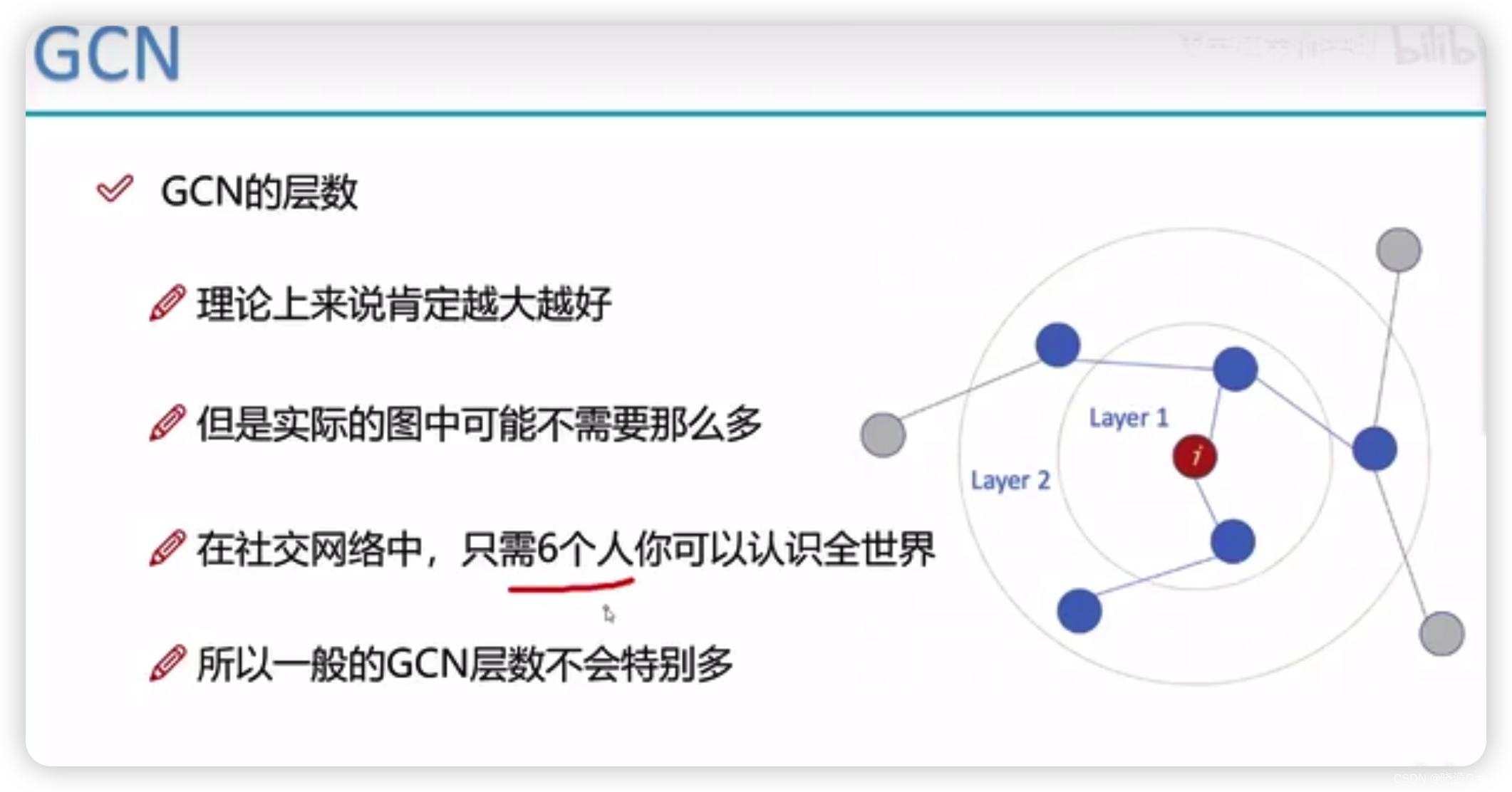
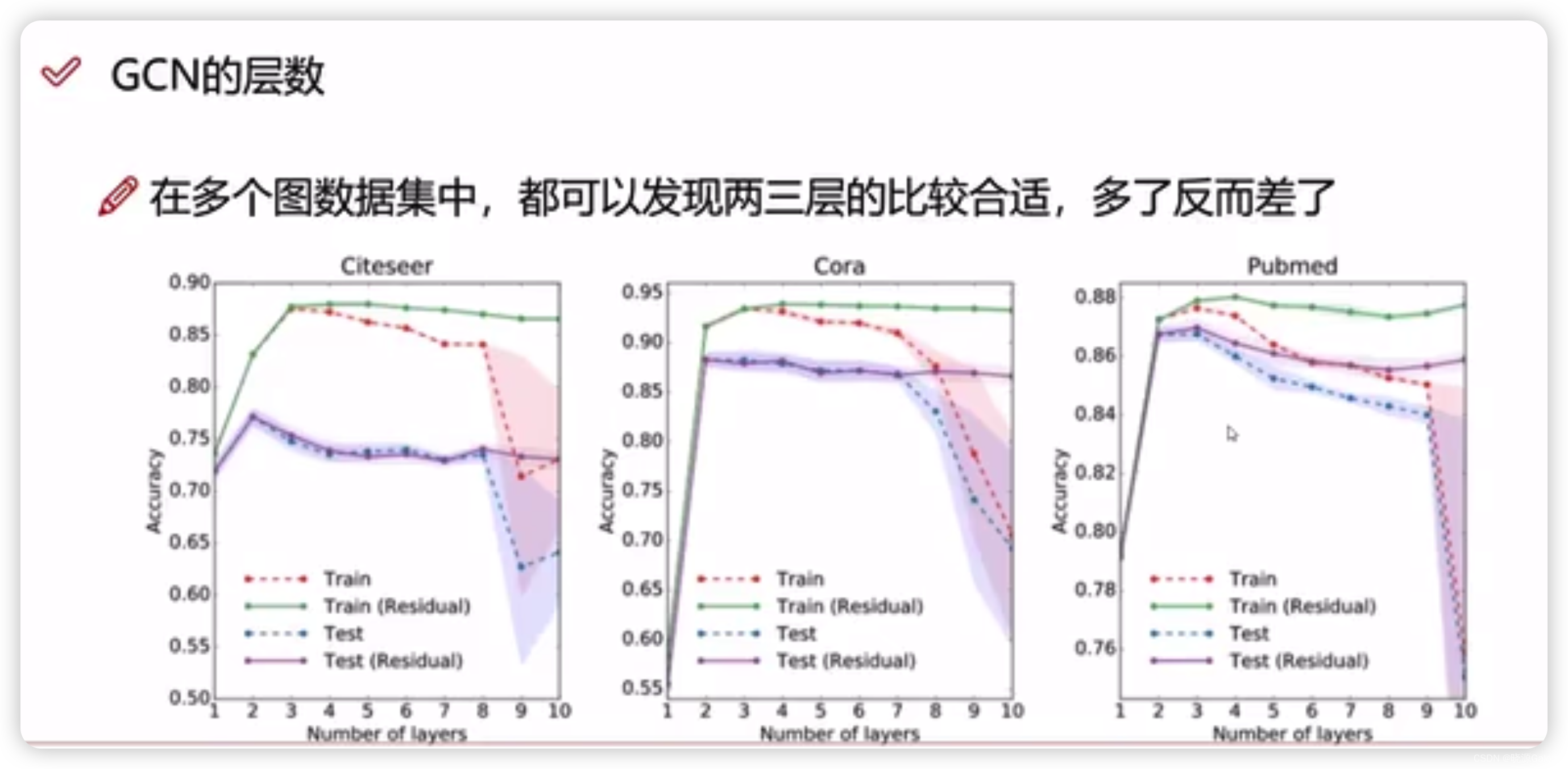
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
图神经网络层数越多效果并不一定越好。（原因可能是某个节点，可能接受到偏远的且和自身属性比较不搭的点的信息）

文章来源:https://blog.csdn.net/Fangyechy/article/details/135443242
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。