回溯算法第二篇(全排列、旅行售货员问题、N皇后)
目录
1. 全排列
题目描述:给定一个不含重复数字的数组?nums?,返回其?所有可能的全排列?。你可以?按任意顺序?返回答案。
示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1] 输出:[[1]]
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums?中的所有整数?互不相同
解决方案如下:
(1)首先画出决策树!
① 开始挖了3个空(如:???),分别对这3个问号填入数字,可以是各个位置可以是1、2或者3。
② 如果第一个位置选1,那么第二个位置就不能选1了,只能选2和3。第一个位置选2或者3也是同理。
③ 总结:每个位置都是独一无二的,在之前不能出现过的。

?(2)设计代码
① 设计三个全局变量。
int[][] ret :一个二维数组,用来存储找到的所有排列结果。
int[] path :这个变量用来存储已经选择的结果,例如一个排列结果是1,2,3,那么 path 数组就存储1,2,3。
boolean[] check :这个变量用来实现“剪枝”操作。将已经归入 path 数组的元素,设置为true,标记为已经使用过,不能再次选择。
② dfs函数(回溯算法的核心)
注意:仅需关系某一个结点在干什么事情。例如在第一次选择可以选择三个元素,第二次只能选择两个元素,第三次只能选择一个元素,这就是每一步需要干的事情。
③ 细节问题
回溯:有两点,第一点干掉 path 最后一个元素;第二点修改check数组。
剪枝
递归出口:遇到叶子结点的时候,直接添加结果。

class Solution {
//定义全局变量 ret 用来收集结果
List<List<Integer>> ret;//用集合来表示二维数组
List<Integer> path;//用来保存每一次结果
boolean[] check;//用来表示某个元素是不是已经被选取过
public List<List<Integer>> permute(int[] nums){
//1.初始化
ret = new ArrayList<>();
path = new ArrayList<>();
check = new boolean[nums.length];
//2.调用dfs(回溯的核心)
dfs(nums);
return ret;
}
public void dfs(int[] nums){
//1.当path的长度和nums的长度一样,那么就是将nums的所有元素已经排列在path里
if(nums.length == path.size()){
ret.add(new ArrayList<>(path));
return;
}
//每一次都有3个选择,只是符不符合的问题
for(int i = 0;i < nums.length;i++){
//正面这个元素还没选取
if(check[i] == false){
path.add(nums[i]);//将这个元素添加到数组中
/*
check还能这么理解:如果一个check的元素为true,也就是来到树的第一层(看上图,有层数注解)
有两个check的元素为true,也就是来到树的第二层
有三个check的元素为true,也就是来到树的第三层
*/
check[i] = true;//将当前位置的元素标记为true,表示已经被选取过了
dfs(nums);
check[i] = false;//将当前位置改为还未选择,具体解析看上图
path.remove(path.size() - 1);//移除最后一个元素
}
}
}
}
2. 旅行售货员问题
题目描述:如下图,一个售货员从0号城市出发,要到1号、2号、3号这几个城市去推销商品,已知各城市之间的路程,问应该如何选定一条从0号城市出发,经过每个城市一遍,最后回到0号城市的路线,使得总的周游路程最小?如下图所示:
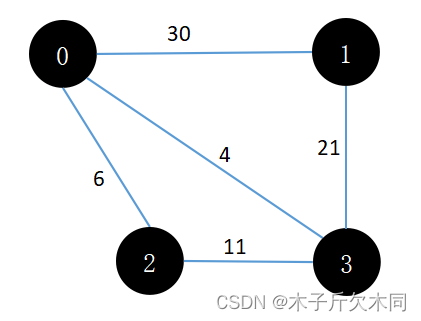
汉密尔顿回路
说白了这就是一个求最短汉密尔顿回路的问题。我们先来了解一下汉密尔顿路径,汉密尔顿回路还有汉密尔顿图
- 汉密尔顿路径:
G= (V,E)是一个图,若G中一条路径通过且仅通过每一个顶点一次,称这条路径为哈密顿路径。- 汉密尔顿回路:
若G中一个回路通过且仅通过每一个顶点一次,称这个环为哈密顿回路。- 汉密尔顿图:
若一个图存在哈密顿回路,就称为哈密顿图。
解决方案如下:
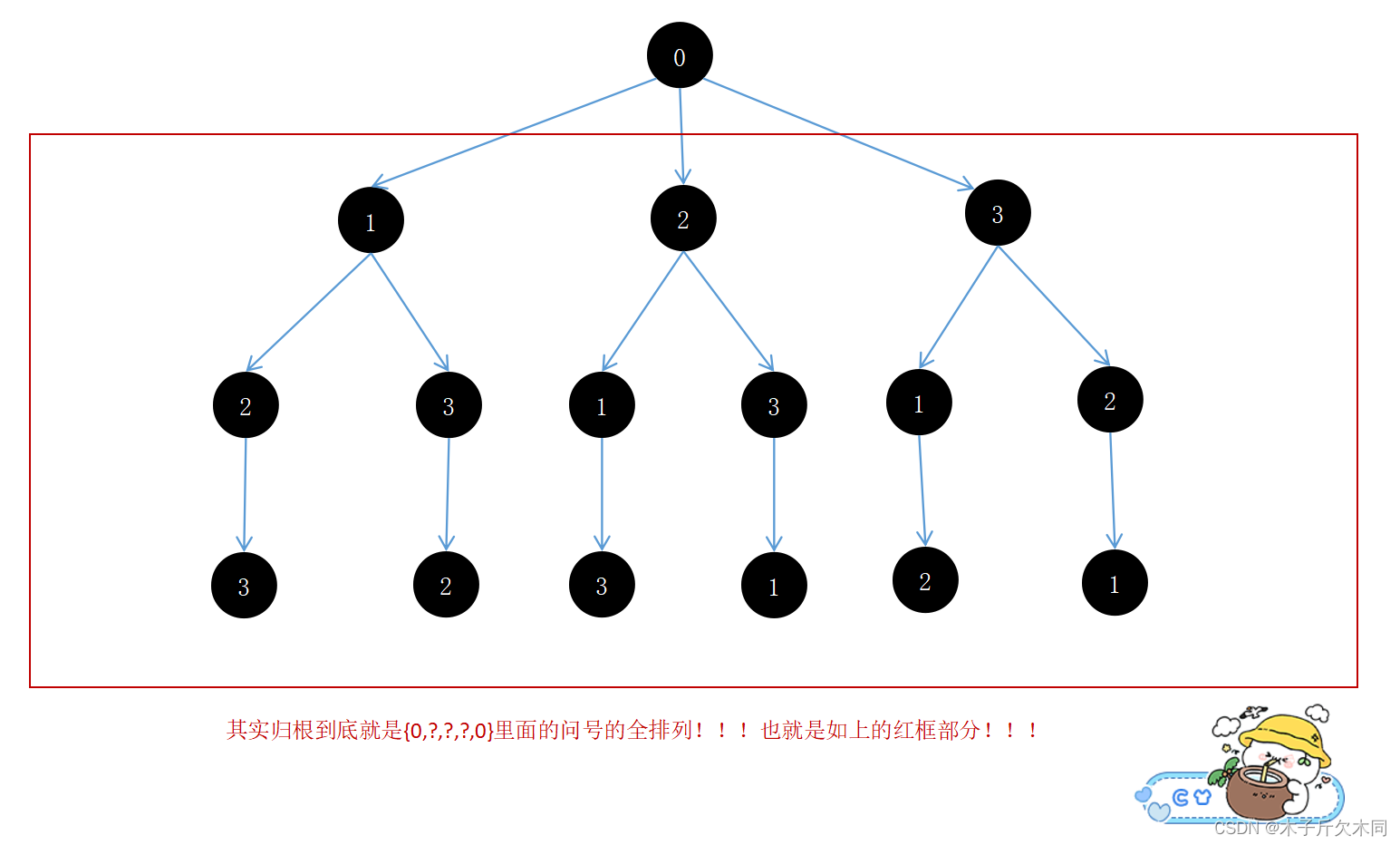
(1)首先画出决策树!
(2)代码设计
① 设计五个全局变量
int[][] ret:用来保存结果。
boolean[] check:用来检查哪个城市已经走过了。
int[] path:用来记录当前的路径。
int[] minPath:用来保存最短路径的数组
int minValue:用来记录最小的总路程
② 有如下几个方法:
public void initGraph():对图进行初始化。
public boolean legal():对路径进行初始判断,是否合法,也就是两个城市zhij。
import java.util.ArrayList;
import java.util.List;
public class Test14 {
//定义全局变量 ret 用来收集结果
int N = 4;
int[] nums = {0, 1, 2, 3};
List<List<Integer>> ret;//用集合来表示二维数组
List<Integer> path;//用来保存每一次结果
boolean[] check;//用来表示某个元素是不是已经被选取过
List<Integer> minPath;//用来保存最短的路径进过的城市
int minValue = Integer.MAX_VALUE;//用来保存最短路程
int[][] graph = new int[N][N];//用来存储图的路径
//为图初始化
public void addEdge(int v1, int v2, int weight) {
graph[v1][v2] = graph[v2][v1] = weight;
}
public void initGraph() {
addEdge(0, 1, 30);
addEdge(0, 2, 6);
addEdge(0, 3, 4);
addEdge(1, 3, 21);
addEdge(2, 3, 11);
}
public List<List<Integer>> permute(int[] nums) {
//1.初始化
ret = new ArrayList<>();
path = new ArrayList<>();
path.add(0);
check = new boolean[nums.length];
minPath = new ArrayList<>();
//2.调用dfs(回溯的核心)
dfs(0, nums);
return ret;
}
//判断路径是否合法
public boolean legal(int index, int n) {
int v1 = path.get(n);//得到当前城市的前一个城市的数组下标
int v2 = index;//当前城市的数组下标
return graph[v1][v2] != 0 && check[index] == false;
}
//判断最后一个城市到达0号城市是否有路径
public boolean legalLast() {
int v1 = path.get(0);
int v2 = path.get(path.size() - 1);
return graph[v1][v2] != 0;
}
public void dfs(int n, int[] nums) {
//证明到达了0号城市之前的最后一个城市
if (n == nums.length - 1) {
//判断最后一个城市到达0号城市是否有路径
if (legalLast()) {
List<Integer> tmp = new ArrayList<>();
for (int i = 0; i < path.size(); i++) {
tmp.add(path.get(i));
}
path.add(0);
tmp.add(path.get(path.size() - 1));
ret.add(new ArrayList<>(tmp));
int tmpRoad = 0;
// tmpRoad 计算本次路程的总和,然后和minValue进行比较
for (int i = 1; i < path.size(); i++) {
int v1 = path.get(i - 1);
int v2 = path.get(i);
tmpRoad += graph[v1][v2];
}
//保留上次的最短路径
int minTmp = minValue;
minValue = Math.min(minValue, tmpRoad);
//如果最短路程和有改变,就将最短路程保留到minPath中
if (minValue != minTmp) {
for (int i = 0; i < path.size(); i++) {
minPath.add(path.get(i));
}
}
}
}
//开始匹配
//从1号城市开始
for (int i = 1; i < nums.length; i++) {
if (legal(i, n)) {
check[i] = true;
path.add(i);
dfs(n + 1, nums);
//恢复现场
check[i] = false;
path.remove(n);
}
}
}
public static void main(String[] args) {
Test14 test14 = new Test14();
test14.initGraph();
test14.permute(test14.nums);
System.out.println(test14.minValue);
for (int i = 0; i < test14.minPath.size(); i++) {
System.out.print(test14.minPath.get(i) + " ");
}
}
}
3. N 皇后
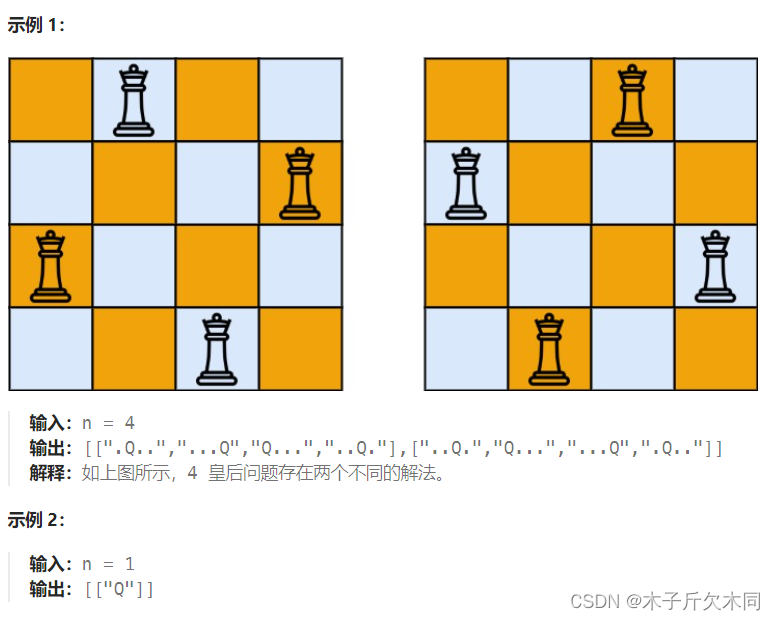
题目描述:按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n?皇后问题?研究的是如何将?n?个皇后放置在?n×n?的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数?n?,返回所有不同的?n?皇后问题?的解决方案。
每一种解法包含一个不同的?n 皇后问题?的棋子放置方案,该方案中?'Q'?和?'.'?分别代表了皇后和空位。
解决方案如下:
(1)算法思路
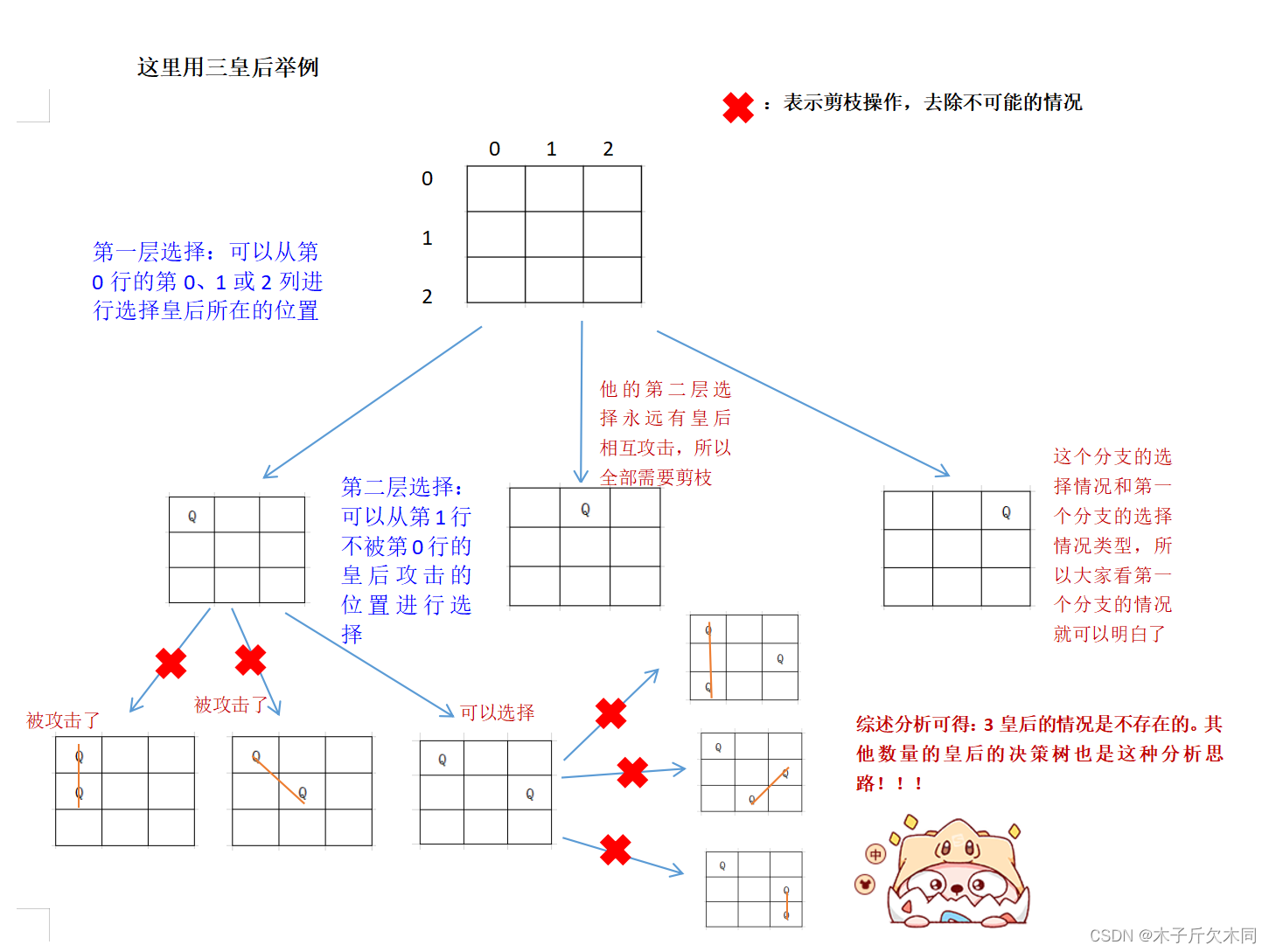
?先,我们在棋盘第??放置第?个皇后,然后遍历棋盘的第??,在可?的位置放置第?个皇后,然后再遍历第三?,在可?的位置放置第三个皇后,以此类推,直到放置了 n 个皇后为?。
我们需要??个数组来记录每??放置的皇后的列数。在每??中,我们尝试放置?个皇后,并检查是否会和前?已经放置的皇后冲突。如果没有冲突,我们就继续递归地放置下??的皇后,直到所有的皇后都放置完毕,然后把这个?案记录下来。
在检查皇后是否冲突时,我们可以??个数组来记录每?列是否已经放置了皇后,并检查当前要放置的皇后是否会和已经放置的皇后冲突。对于对?线,我们可以?两个数组来记录从左上?到右下?的每?条对?线上是否已经放置了皇后,以及从右上?到左下?的每?条对?线上是否已经放置了皇后。
对于对?线是否冲突的判断可以通过以下流程解决:
1. 从左上到右下:相同对?线的?列之差相同。
2. 从右上到左下:相同对?线的?列之和相同。
因此,我们需要创建?于存储解决?案的?维字符串数组 ret,?于存储每个皇后的位置的
?维整数数组? queens ,以及?于记录每?列和对?线上是否已经有皇后的布尔型数组?columns 、diagonals1 和?diagonals2 。


(2)?递归函数流程如下:
① 结束条件:如果?row 等于?n ,则表?已经找到?组解决?案,此时将每个皇后的位置存储到字符串数组?path 中,并将?path 存储到?ret 数组中,然后返回;
② 枚举当前?的每?列,判断该列、两个对?线上是否已经有皇后:
a. 如果有皇后,则继续枚举下?列;
b. 否则,在该位置放置皇后,并将?columns 、diagonals1 和?diagonals2 对应的位置
设为?true ,表?该列和对?线上已经有皇后:递归调? dfs 函数,搜索下??的皇后位置。如果该?案递归结束,则在回溯时需要将 columns 、 diagonals1 和?diagonals2 对应的位置设为?false ,然后继续枚举下?列。
class Solution {
//1.定义全局变量
/*
column:用来判断列的
diagonals1:用来判断正对角线
diagonals2:用来判断反对角线
*/
boolean[] columns, diagonals1, diagonals2;
//结果收集的二维数组
List<List<String>> ret;
//收集"本次"皇后位置的数组,因为棋盘是二维的,所以path是二维数组
char[][] path;
//表示棋盘的行或者列
int n;
//如果要得到八皇后的结果,只需要调用这个方法时,传入8即可
public List<List<String>> solveNQueens(int _n) {
//2.初始化
n = _n;
columns = new boolean[n];
diagonals1 = new boolean[2 * n];
diagonals2 = new boolean[2 * n];
ret = new ArrayList<>();
path = new char[n][n];
//把path的所有位置先该为.
for (int i = 0; i < n; i++) {
Arrays.fill(path[i], '.');
}
//开始回溯算法的核心部分
dfs(0);//从第一行开始
return ret;
}
public void dfs(int row) {
//如果到了棋盘的最后一行了,证明本次皇后们的位置是合法的
if (row == n) {
//添加结果
List<String> tmp = new ArrayList<>();
for (int i = 0; i < n; i++) {
tmp.add(new String(path[i]));
}
ret.add(new ArrayList<>(tmp));
}
//开始匹配
for (int col = 0; col < n; col++) {
//判断能不能放
if (columns[col] == false && diagonals1[col - row + n] == false
&& diagonals2[col + row] == false) {
path[row][col] = 'Q';
columns[col] = diagonals1[col - row + n] =
diagonals2[col + row] = true;
//寻找下一行
dfs(row + 1);
//恢复现场
path[row][col] = '.';
columns[col] = diagonals1[col - row + n]
= diagonals2[col + row] = false;
}
}
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!