[CVPR-23] Instant Volumetric Head Avatars

2023-12-21 22:34:04

[paper | code | proj]?

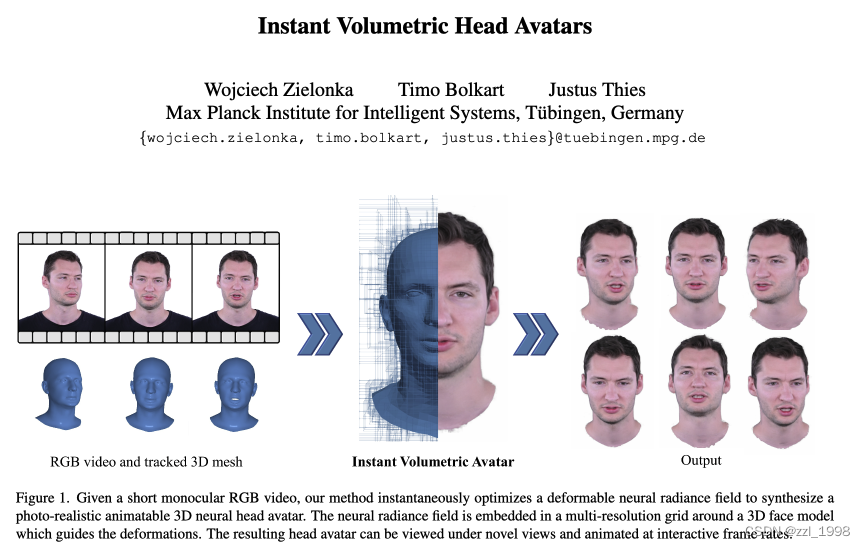
  • 本文提出INSTA。INSTA是一种backward mapping方法。该方法基于NeRF建立标准空间，形变空间（任意表情）通过映射回标准空间，实现渲染。
  • 为实现形变空间中任意点向标准空间的映射，对形变空间中的任意点：1）找到最近邻三角面片；2）通过该三角面片和对应标定空间中的三角面片计算形变梯度；3）通过形变梯度将该点映射回标准空间；
  • 给定一段单目RGB肖像视频，该视频记录了目标人物的不同表情和视角，实现对未见表情和视角的渲染。

快速可变形神经辐射场

  • 任务设置：给定单目视频I = \{I_i\}、相机内参K\in\mathbb{R}^{3\times3}、FLAME meshes?M = \{M_i\}、FLAME表情系数E=\{E_i\}和FLAME相机位姿P=\{P_i\}，生成基于神经辐射场（NeRF）表征的可控制头部虚拟人
  • 本文方法属于Backward Mapping。本文基于NeRF建立标准空间，为了渲染特定面部表情，将形变空间中采样的点，映射回标准空间中。相较而言，经典的Dynamic NeRF是将不同时间的点映射回标准空间。

体渲染

其中，是透明度，\sigma(t)是密度，c(t)是p_t位置的颜色。任意点p_t，在预测其密度和颜色时，会受该帧对应的3DMM表情系数E_i \in \mathbb{R}^{16}影响。

标准空间

本文通过计算形变梯度（deformation gradient）F\in\mathbb{R}^{4\times4}，将形变空间中点映射到标准空间中。

  • 给定第i个形变空间中的任意点，其FLAME最近邻三角面片（triangle）是T_{def} \in M_i，对应标准空间中的FLAME三角面片是T_{canon}\in M^{canon}；
  • 通过三角面片切向量（tangent vector）、双切向量（bitangent vector）和法向量（normal vector），计算旋转矩阵\{R_{canon}, R_{def}\}\in\mathbb{R}^{3\times3}；
  • 通过三角面片顶点可以计算位移\{t_{canon}, t_{def}\}\in\mathbb{R}^3
  • 通过旋转矩阵和位移矩阵，可以计算Frenet坐标系统帧L_{canon}和L_{def}，两者大小都是\mathbb{R}^{4\times4}：

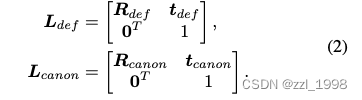
  • 考虑到三角面片在形变空间和标准空间中的差异，本文通过对应三角面片的面积比，计算各向同性的放缩变量\lambda\in\mathbb{R}：\lambda=\frac{a_{def}}{a_{cannon}}
  • 最终，形变梯度F定义如下：

  • 为了避免变化的不连续性，本文额外执行了相邻面片转换的指数加权平均：

  • 其中，，A是T的相邻面片，其中心点为c_f。
  • 值得一提的是，所有顶点的位置都以米为单位（FLAME的度量单位）

为了加速渲染，本文借助经典的bounding volume hierarchy (BVH)，提高最近邻三角面片的搜索速度。同时，为了减缓FLAME中高度密集区域的三角面片搜索，本文简化了研究和眼睛区域；

训练目标

任意点颜色为：

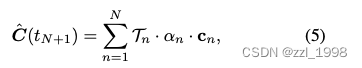
其中，，，\delta_n = \frac{\sqrt{3}}{1024}

借助FLAME模型，实现脸部区域的深度损失：

最终损失为：

?

实验

实验结果

消融实验

文章来源:https://blog.csdn.net/qq_40731332/article/details/135117745
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。