《洛谷深入浅出进阶篇》 组合数学与计数

2023-12-13 13:56:58

本文章篇幅较长，请耐心食用！！

文章一共分为以下几部分：

  • 1，集合与容斥原理

  • 2，常见的组合计数方式

  • 3，二项式定理

  • 4，卡特兰数和斯特林数

  • 前置知识：

  • 加法原理

做一件事情，有n类方法，第一类方法中又有\textbf{m}_\textbf{?{1}}种方法，第二类有\textbf{m}_\textbf{?{2}}种方法…………

第n类有\textbf{m}_\textbf{?{n}}种方法

所以完成这件事情一共有\sum_{i=1}^{n}m_{i}种不同的方案

  • 乘法原理

做一件事情，有n个步骤需要以此完成，

第一步中有\textbf{m}_\textbf{?{1}}种方法，第二步有\textbf{m}_\textbf{?{2}}种方法…………第n类有\textbf{m}_\textbf{?{n}}种方法,

所以完成这件事情一共有\prod_{i=1}^{n}m_{i}种不同的方案

  • 排列数

从n个人里面选出m个人站成一排，考虑每个人的相对位置，总共的方案数就是：

A_{m}^{n} = n\cdot (n-1) \cdot(n-2)\cdot \cdot\cdot\cdot\cdot\cdot =\frac{n!}{(n-m)!}

  • 组合数

从n个人里面挑选出m个人，不需要考虑每个人的相对位置，总共的方案数就是：

C_{n}^{m}=\frac{A_{n}^{m}}{m!}=\frac{n!}{m!\cdot(n-m)!}

一，《集合与容斥》

我们管一个能装下一些互不相同的物品的容器叫做集合

这些被装进容器里的物品必须有明确的定义，即客观的东西。

容器里的物品在你的摇晃之下会改变位置，但是容器依然是那个容器

它们分别是集合的三大特点：确定性，特异性，无序性

集合的世界里只有三种人，自己的子民，其他集合，其他集合的子民

对于自己的子民，例如子民a，集合A的态度是：?a\epsilon A? ? ? 表示a已经是集合A的子民了,对于不是自己国家的子民，A的态度是：a\notin A

其他集合的关系如下：

对于其他集合公主B，她们与集合公主A的关系只有五种：

我自己：A=B

它如同我的傀儡：（B是A的子集）?B\subseteq A

子集又分为：子集，真子集，空集

子集：我自己的一部分，我自己

空集是所有集合的子集，因为它里面啥都没有，就像空气

真子集：我自己的一部分。

它和我有领土纠纷?:? ?A\cap B=c? (c既是A的子民，也是B的子民）

它和我没有领土纠纷：A\bigcup B=A+B（A，B无共同子民）

我竟然只算它的一个傀儡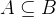！：?A\subseteq B? （可以看成B>=A)

假设整个地球的国家合并到一个集合U里，这个集合U就是全集， 那么U与集合A的关系就是：A\subseteq U

?U=A+C_{U}A?,? 代表着 A 加上?除了A以外的国家 等于整个地球的国家。

容斥原理：

主要内容用三个字概括：求并集！！！！

意思就是，这玩意是给你引入一个公式，然后让你求多个集合的并集。

比如下面这个，怎么求A\bigcup B\bigcup C?

其实你不断用多个集合的交集去加减是可以凑出答案的：

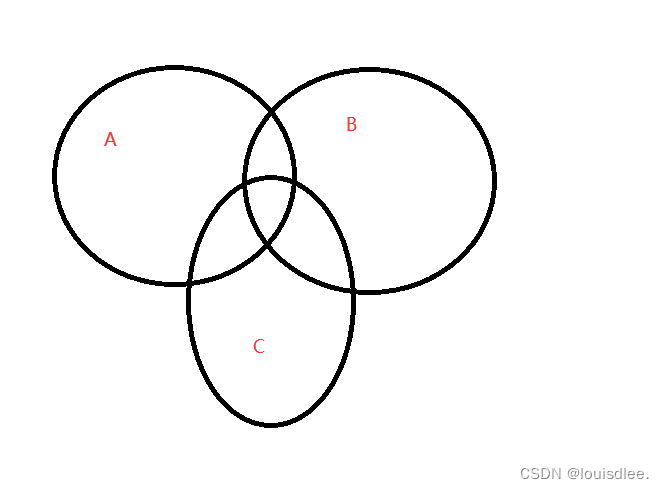
A\bigcup B \bigcup C =|A|+|B|+|C| - A\bigcap B - A\bigcap C -B\bigcap C\ + A\bigcap B\bigcap C

但是呢，聪明的数学家们给出了公式：

| A_{1}\bigcup A_{2}......\bigcup A_{n}| = \sum_{1 \leq i\leq n}A_{i} - \sum_{1\leq i,j\leq n}(A_{i}\bigcap A_{j})..... +(-1)^{n-1}|A_{1}\bigcap A_{2}......\bigcap A_{n}|

用人话讲就是：

奇数集合的交集组合? -? 偶数集合交集组合

啥意思，当集合数量是奇数，例如 1，3，5……? ，每个奇数集合直接任意组合，用\bigcap符号连接

例如：A1，A2，A3? ， A4? 每次挑奇数个集合出来组合，

挑1个，有C（4，1） = 4 种挑法

挑3个，有C（4，3）=4种挑法

减去集合数量是偶数的，例如2，4，6……，每个偶数集合任意组合。

总结：

上述内容讲了以下几点：

1.集合的特性{

特异性

无序性

确定性

}

2.元素与集合的关系{

属于

不属于

}

3.有哪些集合类型{

空集

全集

补集

子集

真子集

}

4.集合与集合的关系{

包含

被包含

相等

不相等

}

5.集合与集合之间的操作{

交集

并集

}

容斥原理的公式，以及它是用来干啥的。

| A_{1}\bigcup A_{2}......\bigcup A_{n}| = \sum_{1 \leq i\leq n}A_{i} - \sum_{1\leq i,j\leq n}(A_{i}\bigcap A_{j})..... +(-1)^{n-1}|A_{1}\bigcap A_{2}......\bigcap A_{n}|

写一道题练练吧！

1，?洛谷P3197 越狱

题目传送门：

P3197 [HNOI2008] 越狱 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)icon-default.png?t=N7T8https://www.luogu.com.cn/problem/P3197

题解：

《深入浅出进阶篇》洛谷P3197 越狱——集合-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134902291?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134902291%22%2C%22source%22%3A%22louisdlee%22%7D

2，洛谷P1287? 盒子与球

传送门：

P1287 盒子与球 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)icon-default.png?t=N7T8https://www.luogu.com.cn/problem/P1287

题解：

洛谷P1287 盒子与球-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134903384?spm=1001.2014.3001.5502


?


3，洛谷P1450 硬币购物?

传送门：

P1450 [HAOI2008] 硬币购物 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)icon-default.png?t=N7T8https://www.luogu.com.cn/problem/P1450

题解：

洛谷P1450 硬币购物-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134908388?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134908388%22%2C%22source%22%3A%22louisdlee%22%7D

?二，常见的组合计数方式

1，插空法

2，错排问题

3，lucas定理

（一些用到的小tips : 求逆元，扩欧，费马小定理）?

1.插空法：

举一个简单的例子。

有7个位置，我们现在要安置3个人，使得这3个人两两不相邻，一共有多少种安插方式？

首先，由题意可知，如果安插3个人，必然有4个空位出现。我们先把这四个空位都拿出来，排成一排。

（在草稿纸上画四个不连续的正方形就可以了）

我们会惊奇的发现，如果我们在正方形中间，或两边空出来的地方插入人的话，那么这些个空位就是天然的屏障，使得两两不相邻。

四个正方形中间有3个空位，第一个空格左边有一个空，最后一个空格右边有一个空，所以总共是五个空。

所以我们只要在这五个空里面插入3个位置就行了，方案就是A（5，3）

2，错排问题：

举例如下：假设我们有n个信封，和n个信箱，编号相同即为投正确。

现在我们要使得，每一个信封都投错，请问一共有多少种投递方式？

判断是否为错排：? 当我们发现每一个信封都有相同数量的投递方式的时候，我们就把它视为一次错排处理。

下面是错排的递推形式：

假设 d（n）为 n 个信封投错的方式 。

此时还未投递，我们任意选一个信封，假设编号为m，那么此时它有（除了对应的信箱m）以外的n-1种投递方法。

假设它投递到了t信箱。

那么对于t信封而言，可以分为，投递给了m信箱，没有投递给m信箱。

投递给了m信箱，那么t，m造成的影响相互抵消，剩下的n-2个信封每个信封的投递方式都是一样的，都是n-3种，所以 剩下的信封的投错的种类为 d（n-2）

如果没有投递给m信箱，那么我们可以发现，t可以投递的信箱是n-2种（不能投m，和其本身），

假设t投递的信箱编号是 q， 那么q可以投递的信箱也是n-2种（可以投m，以及其他n-3种信箱）

最特殊的两个信封的投递种类都是n-2种，那么其他的普通的信封一定也是n-2种。

所以投错情况是 d（n-1）。

综上递推式子为：? （i-1）* （ d（i-1）+d（i-2））

然后初始条件：d（1）=0，d（2）=1 即可。

例题+题解：

洛谷P4071 排列计数-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134913220

3，Lucas定理

不加以证明地给出快速求组合数的方式。

C_{n}^{m} \equiv C_{n\ mod\ p}^{m\ mod \ p}* C_{[\frac{n}{p}]}^{[\frac{m}{p}]} (mod\ p)

化成函数的形式就是：

Lucas(n,m,p)=C_{n}^{m} mod \ p =C_{n\ mod\ p}^{m\ mod\ p}*Lucas(\frac{n}{p},\frac{m}{p},p);

很明显看出是一种递归的 形式

递归的边界就是m==0，返回1.

由于我们前面讲了，组合数公式：C_{n}^{m}=\frac{A_{n}^{m}}{m!}=\frac{n!}{m!\cdot(n-m)!}

所以要求组合数对p取模，分子就要边算阶乘边取模，分母就要求逆元取模。

而求逆元，我们在数论篇已经学过，在这里可以用费马小定理。

例题+题解：

洛谷P3807 Lucas定理-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134927373

三,二项式定理:

不加以证明地给出二项式定理：

(x+y)^{n}= \sum_{i=0}^{n}C_{n}^{i}*x^{i}*y^{n-i}

理解也很简单，就是用组合的思想——口袋法。

假设你有n个口袋，口袋里装了2个球，一个是x，一个是y。

第一项就是从所有口袋中掏出0个x，和n个y? 的掏法：C_{n}^{0}*x^{0}*y^{n}?

第二项就是掏出1个x，和掏出n-1个y 有多少种掏法：C_{n}^{1}*x^{1}*y^{n-1}

…………

第i项就是掏出i-1个x，和掏出n-i+1个y的掏法：C_{n}^{i-1}*x^{i-1}*y^{n-i+1}

累加起来，就是(x+y)^{n}= \sum_{i=0}^{n}C_{n}^{i}*x^{i}*y^{n-i}

例题：

洛谷P1313 计算系数-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134930342?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134930342%22%2C%22source%22%3A%22louisdlee%22%7D

四，卡特兰数与斯特林数

卡特兰数可以看这篇讲解：

要永远相信你的灵魂——卡特兰数-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134212397?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522170228497216800182190983%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=170228497216800182190983&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~first_rank_ecpm_v1~rank_v31_ecpm-1-134212397-null-null.nonecase&utm_term=%E5%8D%A1%E7%89%B9%E5%85%B0&spm=1018.2226.3001.4450

当我们有两种不同的操作，并且这两种操作是有限制的，即一种操作的进行次数绝不能大于另一种（这种限制可能会给出，也可能隐藏在条件中）

此时我们可以考虑用卡特兰数的递归式子：

K_{n}=\sum _{i=0}^{n}K_{i}*K_{n-i-1}=K_{0}K_{n-1}+K_{1}K_{n-2}+.....K_{n-1}K_{0}

或者递推式子：

K_{n}=\frac{4n-2}{n+1}K_{n-1}

通项公式：

K_{n}=C_{2n}^{n}-C_{2n}^{n-1}=\frac{1}{n+1}C_{2n}^{n}

（如果n过大，不是高精度就是取模，如果取模的话，推荐用不带除法的式子，这样可以不算逆元）

例题+题解：??

P1044 [NOIP2003 普及组] 栈——卡特兰数-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134946261?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134946261%22%2C%22source%22%3A%22louisdlee%22%7D

洛谷P1722 矩阵Ⅱ——卡特兰数-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134962197?spm=1001.2014.3001.5502

斯特林数：

《洛谷深入浅出》斯特林数-CSDN博客icon-default.png?t=N7T8https://blog.csdn.net/louisdlee/article/details/134962264?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134962264%22%2C%22source%22%3A%22louisdlee%22%7D

文章来源:https://blog.csdn.net/louisdlee/article/details/134899348
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。