力扣日记12.27-【二叉树篇】235. 二叉搜索树的最近公共祖先
力扣日记:【二叉树篇】235. 二叉搜索树的最近公共祖先
日期:2023.12.27
参考:代码随想录、力扣
235. 二叉搜索树的最近公共祖先
题目描述
难度:中等
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
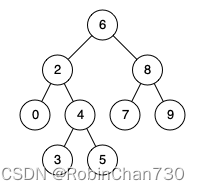
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
#define SOLUTION 2
public:
#if SOLUTION == 1
// 不考虑二叉搜索树特性
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL || root == p || root == q) return root;
// 左
TreeNode* left = lowestCommonAncestor(root->left, p, q);
// 右
TreeNode* right = lowestCommonAncestor(root->right, p, q);
// 中
if (left != NULL && right != NULL) return root; // 左右都出p或q,则root为公共祖先
if (left == NULL) return right; // 左为空,则右不为空或为空都是right
return left; // 左边同理
}
#elif SOLUTION == 2
// 考虑二叉搜索树特性
// 二叉搜索树不需要通过后序遍历,利用其“左子树小于根、右子树大于根”的特性,可得以下结论:
// 情况1:如果 root本身就是p或q,则root就是公共祖先
// 情况2:如果 p->val < root->val < q->val 或反之,则 root 一定是 p 和 q 的最近公共祖先(root在p和q之间 /\ )
// 情况3:如果 root 的值比 p 和 q 都大,则 p 和 q 在 root 的左子树中,公共祖先也一定在左子树中,则往左递归
// 情况4:如果 root 的值比 p 和 q 都小,则与情况2同理
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
/*
if (root == p || root == q) return root;
if ((root->val > p->val && root->val < q->val) || (root->val > q->val && root->val < p->val)) return root;
if (root->val > p->val && root->val > q->val) return lowestCommonAncestor(root->left, p, q);
if (root->val < p->val && root->val < q->val) return lowestCommonAncestor(root->right, p, q);
return NULL; // 不加这个会报错
*/
// 更简便的写法
// 公共祖先在左子树
if (root->val > p->val && root->val > q->val) return lowestCommonAncestor(root->left, p, q);
// 公共祖先在右子树
else if (root->val < p->val && root->val < q->val) return lowestCommonAncestor(root->right, p, q);
// root 即为公共祖先
else return root; // 剩下就是 root->val >= p->val && root->val <= q->val 或反之的情况
}
#elif SOLUTION == 3
// 迭代法
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while (root != NULL) {
// 1. 公共祖先在左子树,往左遍历
if (root->val > p->val && root->val > q->val) root = root->left;
// 2. 公共祖先在右子树,往右遍历
else if (root->val < p->val && root->val < q->val) root = root->right;
// 其余情况,直接返回
else return root;
}
return NULL;
}
#endif
};
复杂度
时间复杂度:
空间复杂度:
思路总结
- 考虑二叉搜索树特性
- 二叉搜索树不需要通过后序遍历,利用其“左子树小于根、右子树大于根”的特性,对几种情况进行分析即可:
-
情况1:如果 root本身就是p或q,则root就是公共祖先
-
情况2:如果 p->val < root->val < q->val 或反之,则 root 一定是 p 和 q 的最近公共祖先(root在p和q之间 /\ )
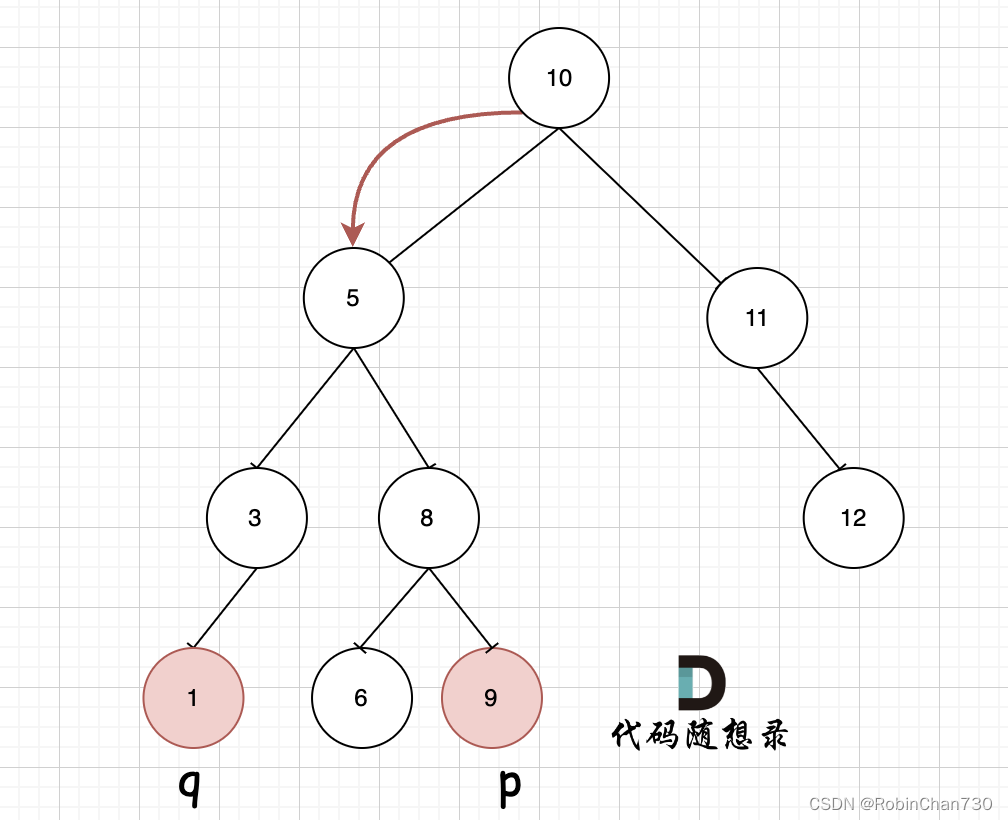
如图,从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
所以当我们从上向下去递归遍历,第一次遇到 cur节点是数值在[q, p]区间中,那么cur就是 q和p的最近公共祖先。
—— by 代码随想录 -
情况3:如果 root 的值比 p 和 q 都大,则 p 和 q 在 root 的左子树中,公共祖先也一定在左子树中,则往左递归
-
情况4:如果 root 的值比 p 和 q 都小,则与情况2同理,往右递归
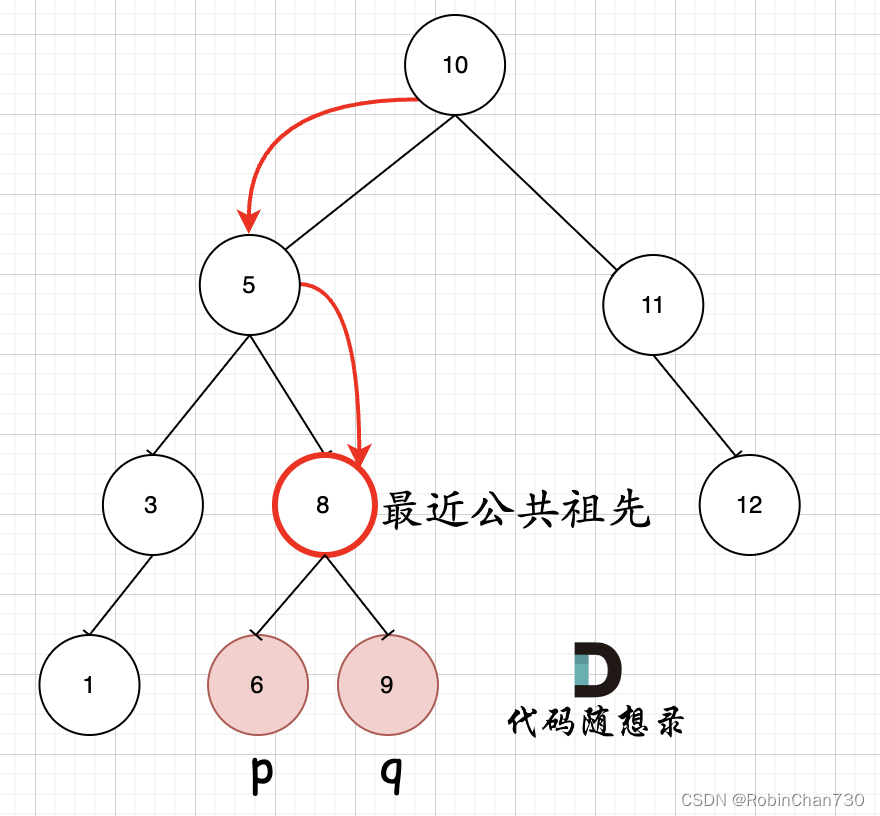
-
- 且相比普通二叉树写法,本题在找到最近公共祖先后,直接返回,而不是像SOLUTION-1那样,要左边和右边都递归好,再返回。即只需要搜索一边即可,不需要搜索一整棵树。
- 记录 代码随想录 中:
- 搜索一条边的写法:
if (递归函数(root->left)) return ; if (递归函数(root->right)) return ;- 搜索整个树写法:
left = 递归函数(root->left); right = 递归函数(root->right); left与right的逻辑处理;- 本题就是标准的搜索一条边的写法,遇到递归函数的返回值,如果不为空,立刻返回。
- 迭代也是相同的思路
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!