生存分析序章1——解析生存分析:探寻时间与事件的奥秘
写在开头
生存分析,作为统计学和生物学交汇的领域,旨在探究时间与事件之间的奥秘。这一领域的深入研究不仅在医学和生物学领域有着广泛的应用,同时在数据分析和数据挖掘中也发挥着关键作用。
1 基本概念
1.1 什么是生存分析
生存分析,又称生存时间分析或事件史分析,是一种统计学方法,专注于分析个体在不同时间点经历某个事件的概率。这个事件可以是任何有明确定义的终点,比如生病、死亡、设备故障等。其背后的核心思想是研究个体的生存经验,了解事件发生的概率随时间的推移而如何变化。
1.2 能解决哪些问题
-
事件时间分布: 生存分析可以用来估计个体经历特定事件的时间分布,例如生命终点、产品故障等。
-
比较生存曲线: 生存分析允许比较不同群体、治疗组和对照组的生存曲线,以评估干预措施的效果。
-
危险因素: 生存分析可以识别和量化影响生存时间的危险因素,这些危险因素可以是疾病特征、治疗方案或其他相关因素。
-
时间相关性: 生存分析考虑了时间的因素,可以更全面地理解事件发生的时间模式和动态。
1.3 一般步骤
生存分析的一般步骤如下:
-
收集数据:
- 获取包含个体信息、事件发生时间以及相关协变量(如年龄、性别、治疗方案等)的数据。
-
数据清理与准备:
- 处理缺失数据:识别并处理缺失的事件时间或协变量数据。
- 处理异常值:检查并纠正可能影响结果的异常值。
-
定义事件和时间:
- 确定研究的事件,例如生病、死亡或设备故障。
- 定义时间尺度,即确定观察的时间单位,如天、月、年等。
-
生成生存数据集:
- 根据数据,生成生存分析所需的数据集,包括个体ID、事件发生时间、事件发生状态(发生/未发生)、协变量等。
-
描述性统计分析:
- 绘制生存曲线:使用Kaplan-Meier方法,绘制整体生存曲线,了解样本中个体生存的概率随时间的变化。
- 计算中位生存时间:中位生存时间是指在某一时间点上一半的个体发生了事件。
-
差异性检验:
- 使用统计检验方法(如log-rank检验)比较不同组别(如治疗组与对照组)的生存曲线,判断是否存在显著差异。
-
拟合生存模型:
- 使用Cox比例风险模型等生存模型,探索协变量对事件风险的影响。这可以帮助识别潜在的预测因子。
-
模型评估:
- 评估模型的拟合优度,检查模型是否适用于数据。
- 根据需要进行模型调整,例如加入交互项或进行变量选择。
-
预测和解释:
- 基于建立的模型,进行事件发生的概率预测。
- 解释协变量对事件的影响,理解其在生存分析中的作用。
-
报告和解释结果:
- 撰写生存分析结果的报告,包括生存曲线、模型参数、显著性检验的结果等。
- 将结果解释为实际应用背景,为决策提供支持。
1.4 核心概念
1.4.1 生存函数
生存函数 S ( t ) S(t) S(t) 描述了在给定时间 t t t 之后个体尚未经历事件(生存)的概率。数学上,生存函数可以表示为:
S ( t ) = P ( T > t ) S(t) = P(T > t) S(t)=P(T>t)
其中, T T T 是表示个体经历事件的随机变量。生存函数通常在时间点 t t t 处于风险集中的个体中计算。
通过上面的公式,我们在任意给定时间点,得出个体尚未经历事件的概率。生存函数的图形通常是递减的,反映了随着时间的推移,生存的概率逐渐减小。在描述不同群体、治疗组与对照组等在不同时间点上的生存经验时非常有用。
1.4.2 累计风险
累积风险 H ( t ) H(t) H(t) 描述了在时间 t t t 之前发生事件的累积概率,是生存函数的补充。累积风险与生存函数之间的关系如下:
H ( t ) = ? ln ? ( S ( t ) ) H(t) = -\ln(S(t)) H(t)=?ln(S(t))
或者等价地,生存函数可以通过累积风险的指数函数表示:
S ( t ) = e ? H ( t ) S(t) = e^{-H(t)} S(t)=e?H(t)
累积风险提供了观察到时间 t t t 处于风险集中的个体经历事件的总体风险。它的增加表明在过去的时间段内发生事件的累积概率。
1.4.3 生存曲线
生存曲线是生存函数的图形表示,用于可视化在不同时间点上个体生存的概率。在 Kaplan-Meier 生存分析中,生存曲线通过观察到的生存概率估计得出。生存曲线的形状和趋势反映了个体在不同时间点的生存经验,例如曲线下降可能表示事件风险增加。
生存曲线以时间为横轴,生存函数或生存概率为纵轴,通过观测到的数据点绘制而成。
1.4.4 风险比
风险比用于比较两个或多个组别之间的事件风险。在 Cox 比例风险模型中,风险比的基本形式为:
H R = e β HR = e^{\beta} HR=eβ
其中, β \beta β 是协变量的系数。风险比等于1表示两个组别的事件风险相等;大于1表示事件风险增加,小于1表示事件风险减少。风险比是评估不同协变量对事件发生概率影响的关键指标。
1.4.5 中位生存时间
中位生存时间是指在生存曲线上50%的个体经历事件所需的时间。它是一个描述集体生存经验的重要指标。中位生存时间提供了一个描述集体生存经验的指标,它并不受极端值的影响。常用于比较不同治疗方案或不同群体在事件发生方面的效果。
1.4.6 Censored Data(截尾数据)
在生存分析中,有时个体并未在观察期间经历事件,或者个体在观察期间失去了联系。这种情况下的数据被称为截尾数据,通常用符号 “C” 表示。截尾数据可能发生在实验结束时、个体退出研究、或者观察期结束时,这时候我们不能准确地得知个体何时经历了事件。在生存分析中,需要采用合适的方法来处理截尾数据,以确保模型的准确性和可靠性。
以下是一些常见的处理截尾数据的方法:
-
1).截断生存分析(Truncated Survival Analysis):
-
方法: 在截断生存分析中,只考虑在某个时间点之前观察到的数据。即,只包括在观察期间没有发生事件或者在某个时间点之前发生事件的个体。
-
适用情况: 当失访或截尾数据的出现是随机的,并且不与研究中的其他因素相关时,截断生存分析是一个有效的方法。
-
-
2).Cox 比例风险模型中的加权方法:
-
方法: 在 Cox 比例风险模型中,可以使用加权方法来调整失访个体的权重,以尽量减小因失访而引入的偏差。
-
适用情况: 适用于失访是非随机的情况,且能够获得关于失访原因和模型中其他协变量的信息。
-
-
3).Kaplan-Meier 曲线和 Log-Rank 检验:
-
方法: 使用 Kaplan-Meier 生存曲线和 Log-Rank 检验,比较不同组别的生存曲线,评估失访是否对结果产生显著影响。
-
适用情况: 适用于失访是随机的情况,可以通过比较生存曲线来初步评估失访对结果的潜在影响。
-
-
4).多重截断:
-
方法: 将观察期间的时间分段,对每个时间段内失访的个体进行分析,以检测失访对生存分析结果的影响。
-
适用情况: 适用于观察期间存在多次失访或截尾的情况,可以更精细地了解失访对不同时间段的影响。
-
-
5).敏感性分析:
-
方法: 进行敏感性分析,评估失访对结果的敏感性。可以尝试不同的失访假设,检查结果的稳健性。
-
适用情况: 适用于失访原因和失访机制不清楚的情况,通过敏感性分析来探讨不同假设下的结果变化。
-
2 生存分析的重要性
生存分析是一种重要的统计方法,主要用于研究个体在一定时间内经历某个事件的概率。其重要性体现在多个领域,包括医学、流行病学、工程和产业等。在疾病研究中,生存分析用于评估治疗效果、预测患者生存期望,对危险因素进行分析,为医疗决策提供科学依据。在工业领域,生存分析应用于研究设备寿命、预测故障时间,有助于提高设备可靠性,优化维护策略。以下将从对疾病研究的应用和工业领域两个方面详细描述生存分析的重要性。
2.1 对疾病研究的应用
在医学领域,生存分析具有重要的应用,主要体现在以下几个方面:
-
治疗效果评估:
-
应用: 生存分析在疾病研究中被广泛用于评估不同治疗方案对患者生存时间的影响。通过绘制生存曲线和进行统计分析,可以比较不同治疗组之间生存的差异。
-
优势: 提供了客观的、可量化的治疗效果评估,有助于医生和研究者选择最有效的治疗方案,提高治疗成功率。
-
-
生存期望预测:
-
应用: 生存分析通过研究患者的生存曲线和中位生存时间,可以预测患者的生存期望。这有助于医生向患者提供更准确的预后信息。
-
优势: 增强患者对疾病发展的认识,帮助患者更好地规划治疗和生活,提高心理适应水平。
-
-
危险因素分析:
-
应用: 生存分析用于确定可能影响患者生存的危险因素,如年龄、性别、病理特征等。通过 Cox 比例风险模型等方法,可以估计各个因素对生存的相对影响。
-
优势: 为个体化医疗提供依据,支持医生制定更精准的治疗方案,提高治疗效果。
-
2.2 工业领域的应用
在工业领域,生存分析同样具有重要的应用价值:
-
设备寿命研究:
-
应用: 生存分析可用于评估工业设备的寿命分布。通过监测设备故障和失效的时间,企业能够了解设备的可靠性和使用寿命。
-
优势: 提供科学的依据,帮助企业制定更合理的设备维护计划和更新策略,减少因设备故障而导致的生产中断。
-
-
故障预测与维护优化:
-
应用: 通过生存分析,企业可以预测设备故障的发生概率,并制定相应的维护计划。这有助于优化维护策略,降低维护成本。
-
优势: 降低了因突发故障而引起的生产线停机风险,提高了生产效率和设备利用率。
-
-
质量控制与改进:
-
应用: 生存分析可用于监测产品的质量状况,及时发现潜在的质量问题。通过分析产品失效的时间分布,可以预测产品的质量寿命。
-
优势: 有助于企业实施精益生产和持续改进,提高产品质量和客户满意度。
-
2.3 商业领域的应用
虽然说生存分析起源于医学领域,但是依然可以应用在商业领域,主要体现在以下几个方面:
-
客户生命周期价值分析:
-
应用: 生存分析可以用于评估客户在商业中的生命周期,包括首次购买到最后一次交易的时间跨度。通过分析客户生存曲线,企业可以了解客户的维持时间和购买频率,从而估算客户的生命周期价值。
-
优势: 基于客户的生命周期信息,企业可以制定更有效的客户保留和推广策略,提高客户满意度,实现更好的营销投资回报率。
-
-
产品寿命周期分析:
-
应用: 生存分析可用于评估产品的生命周期,并帮助企业预测产品的市场寿命。通过分析产品的生存曲线,企业可以更好地了解产品的推出、成熟和衰退阶段。
-
优势: 这有助于企业及时调整产品策略,合理安排库存,优化生产计划,降低过期库存的风险,并更好地满足市场需求。
-
-
员工留存分析:
-
应用: 生存分析可用于评估员工在公司内的留存时间,帮助企业了解员工的流动情况和员工留存率。通过分析员工的生存曲线,企业可以发现和解决员工流失的潜在问题。
-
优势: 通过提前识别可能离职的员工,企业可以采取措施,如提供培训、晋升机会或改善工作环境,从而提高员工满意度和留存率。
-
-
项目完成时间分析:
-
应用: 生存分析可用于分析项目完成的时间分布,帮助企业更好地估算项目完成的时间和提高项目管理的效率。
-
优势: 通过识别可能导致项目延期的因素,企业可以在项目早期采取纠正措施,降低项目失败的风险。
-
-
市场竞争分析:
-
应用: 生存分析可以用于评估市场上竞争对手的生存时间,帮助企业了解竞争格局和预测竞争对手可能采取的策略。
-
优势: 通过分析竞争对手的生存曲线,企业可以更好地制定市场策略,应对激烈竞争,提高市场份额。
-
3 方法与工具
3.1 Kaplan-Meier 曲线
Kaplan-Meier 曲线是生存分析中一种常用的非参数统计方法,用于估计患者或个体在一定时间内生存下来的概率。下图是一个简单的例子:
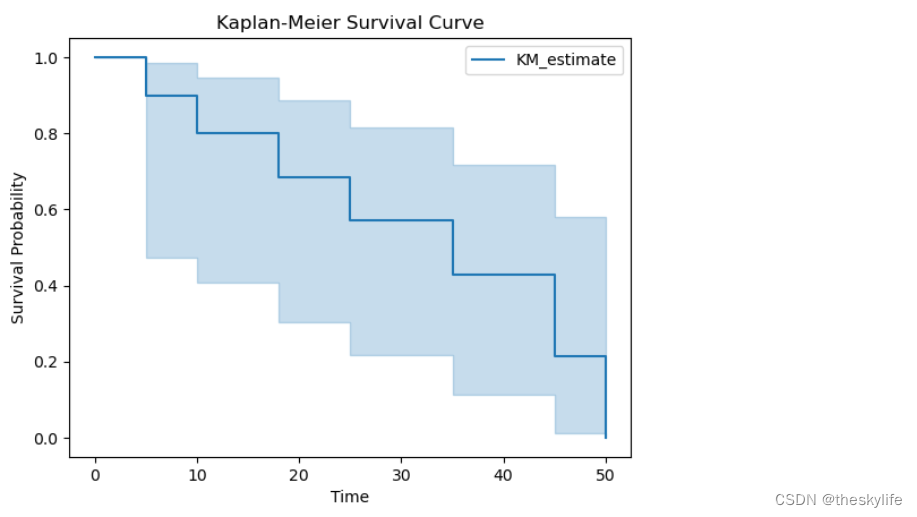
Kaplan-Meier 曲线的生成步骤
-
确定分析起始时间点: 选择开始观察的时间点,通常是事件发生的时间点或研究的起始时间。
-
确定终点时间和事件: 对于每个个体,确定观察的终点时间(生存时间的最大观察时间)和是否发生感兴趣的事件。事件可以是死亡、疾病复发或其他定义的终点。
-
计算生存概率: 对于每个时间点,计算在该时间点前生存下来的个体比例。生存概率(Survival Probability)是指在给定时间内个体生存的概率。
-
绘制累积生存曲线: 将每个时间点的生存概率绘制在图上,连接它们形成Kaplan-Meier 曲线。曲线的上升表示生存,曲线下降表示事件(死亡或其他终点)的发生。
Kaplan-Meier 曲线的特点
-
右侧截尾: Kaplan-Meier 曲线通常在数据集中的最后一个生存时间点截尾,即在最后一个观察时间点之后,曲线不再下降。
-
每次事件都有影响: 每次事件(死亡或其他终点)都对曲线产生影响,使得曲线下降。
-
无需假设分布: 与一些参数统计方法不同,Kaplan-Meier 曲线是一种非参数方法,不对生存时间分布做出任何假设,适用于各种生存数据的分析。
Kaplan-Meier 曲线的解读
-
曲线上的每个点表示一个观察时间点,纵坐标表示在该时间点前生存下来的患者比例。
-
曲线下降的越快,说明事件的累积发生率越高,生存概率越低。
-
曲线上的95%置信区间表示估计的不确定性,帮助评估估计的可靠性。
3.2 Cox 比例风险模型
Cox 比例风险模型(Cox Proportional-Hazards Model)是一种用于生存分析的半参数统计模型,用于研究一个或多个协变量(covariates)对生存时间的影响。
Cox 比例风险模型的基本形式
Cox 比例风险模型假设个体的风险是一个基线风险函数(baseline hazard function)和一个关于协变量的相对风险函数(relative hazard function)的乘积。模型的基本形式如下:
h ( t , X ) = h 0 ( t ) ? exp ? ( β 1 X 1 + β 2 X 2 + … + β k X k ) h(t, \mathbf{X}) = h_0(t) \cdot \exp(\beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_k X_k) h(t,X)=h0?(t)?exp(β1?X1?+β2?X2?+…+βk?Xk?)
其中:
-
h ( t , X ) h(t, \mathbf{X}) h(t,X) 是时间 t t t 处的风险函数。
-
h 0 ( t ) h_0(t) h0?(t) 是基线风险函数,表示在协变量 X \mathbf{X} X 取零时的风险。
-
β 1 , β 2 , … , β k \beta_1, \beta_2, \ldots, \beta_k β1?,β2?,…,βk? 是协变量 X 1 , X 2 , … , X k X_1, X_2, \ldots, X_k X1?,X2?,…,Xk? 的系数,表示相对风险的对数。
-
exp ? ( β 1 X 1 + β 2 X 2 + … + β k X k ) \exp(\beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_k X_k) exp(β1?X1?+β2?X2?+…+βk?Xk?) 表示相对风险的比例,即相对于基线风险的比例。
Cox 比例风险模型的特点
-
半参数性质: Cox 比例风险模型是半参数模型,因为它对基线风险函数的形式不做具体的假设,而是通过估计协变量的系数来捕捉相对风险的变化。
-
相对风险: 模型的关键部分是相对风险的比例,它表示协变量的改变如何影响风险。如果 exp ? ( β i ) > 1 \exp(\beta_i) > 1 exp(βi?)>1,则表示增加 X i X_i Xi? 会增加风险,如果 exp ? ( β i ) < 1 \exp(\beta_i) < 1 exp(βi?)<1,则表示增加 X i X_i Xi? 会减小风险。
-
不假定基线风险: Cox 模型的一个优点是不需要对基线风险函数做出具体的假设,因此适用于各种不同的生存数据。
Cox 比例风险模型的解释
Cox 比例风险模型的模型摘要中包含了一些重要的信息,其中最关键的是协变量的系数(coefficients)和相对风险比(hazard ratios)。以下是模型摘要的一些主要部分:
-
协变量系数: 模型摘要中会显示每个协变量的系数(coefficients),例如
covariate1和covariate2。这些系数表示对数风险的变化量。 -
相对风险比(Hazard Ratios): 每个协变量的相对风险比是指 exp ? ( 系数 ) \exp(\text{系数}) exp(系数)。如果相对风险比为1,则表示该协变量对风险没有影响;如果相对风险比大于1,表示协变量的增加与增加风险有关;如果相对风险比小于1,表示协变量的增加与减少风险有关。
-
p-值: 摘要中通常还包括每个协变量系数的p-值。p-值用于检验某个协变量的系数是否显著不同于零。如果p-值小于显著性水平(通常为0.05),则表示协变量对生存有显著影响。
-
置信区间: 伴随每个系数的是95%的置信区间。这表示我们对相对风险比的估计是有一定不确定性的,区间越窄表示估计越精确。
在解释Cox模型时需要注意的事项
-
系数的正负和相对风险比的大小并不总是直观的。在解释结果时,应该考虑协变量的实际含义以及是否符合领域知识。
-
p-值和置信区间提供了关于系数的显著性和不确定性的信息。小的p-值和窄的置信区间通常表示更可靠的估计。
-
Cox 模型的假设之一是比例风险假设,即相对风险比是常数。检查模型的假设是否成立很重要,可以通过绘制累积残差图等方式来评估。
-
在使用Cox模型时,必须注意协变量的选择,过多的协变量可能导致过拟合,而过少可能忽略重要的影响因素。
写在最后
生存分析的局限性
尽管生存分析在许多领域都有着卓越的应用,但它也有一些局限性。比如,它通常假设个体的生存经验是相互独立的,这在某些情况下可能不成立。
未来发展方向
随着数据科学和机器学习的迅猛发展,未来生存分析可能更加注重结合更多的数据源和模型,提高预测的准确性。同时,更加复杂的时间相关性和动态风险模型也可能成为未来的研究方向。
总体而言,生存分析作为一门强大的统计工具,不仅在医学领域有着深远的影响,也在数据分析和数据挖掘中展现了巨大的潜力。通过深入理解生存分析的基本概念和工具,我们能更好地应用这一奥秘的统计学方法,为各个领域带来更准确的预测和决策支持。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!