时序预测 | Matlab基于灰色隐马尔可夫模型(HMMP-GM11)的时间序列预测

2024-01-09 20:28:05

时序预测 | Matlab基于灰色隐马尔可夫模型(HMMP-GM11)的时间序列预测

目录

预测效果

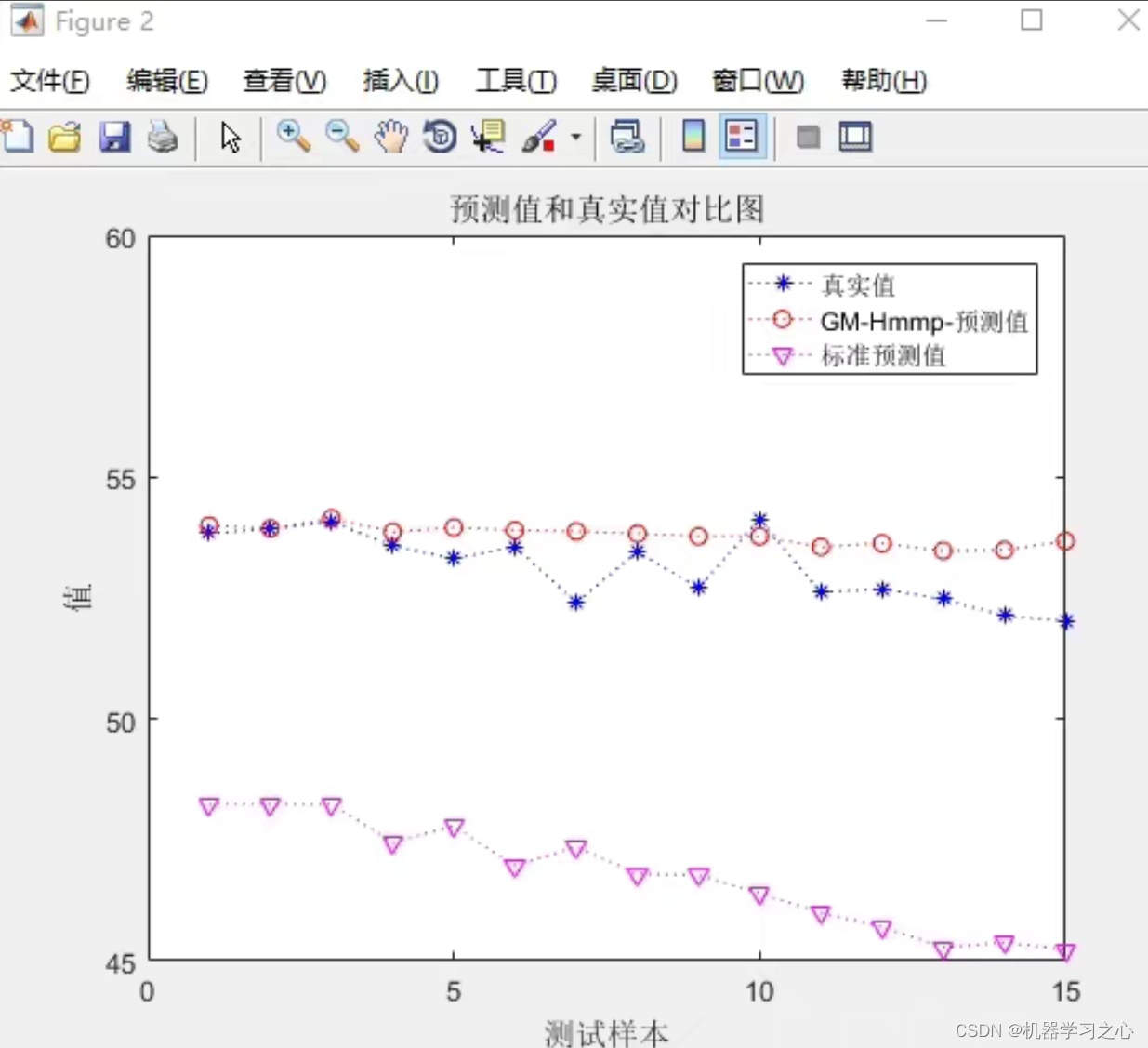
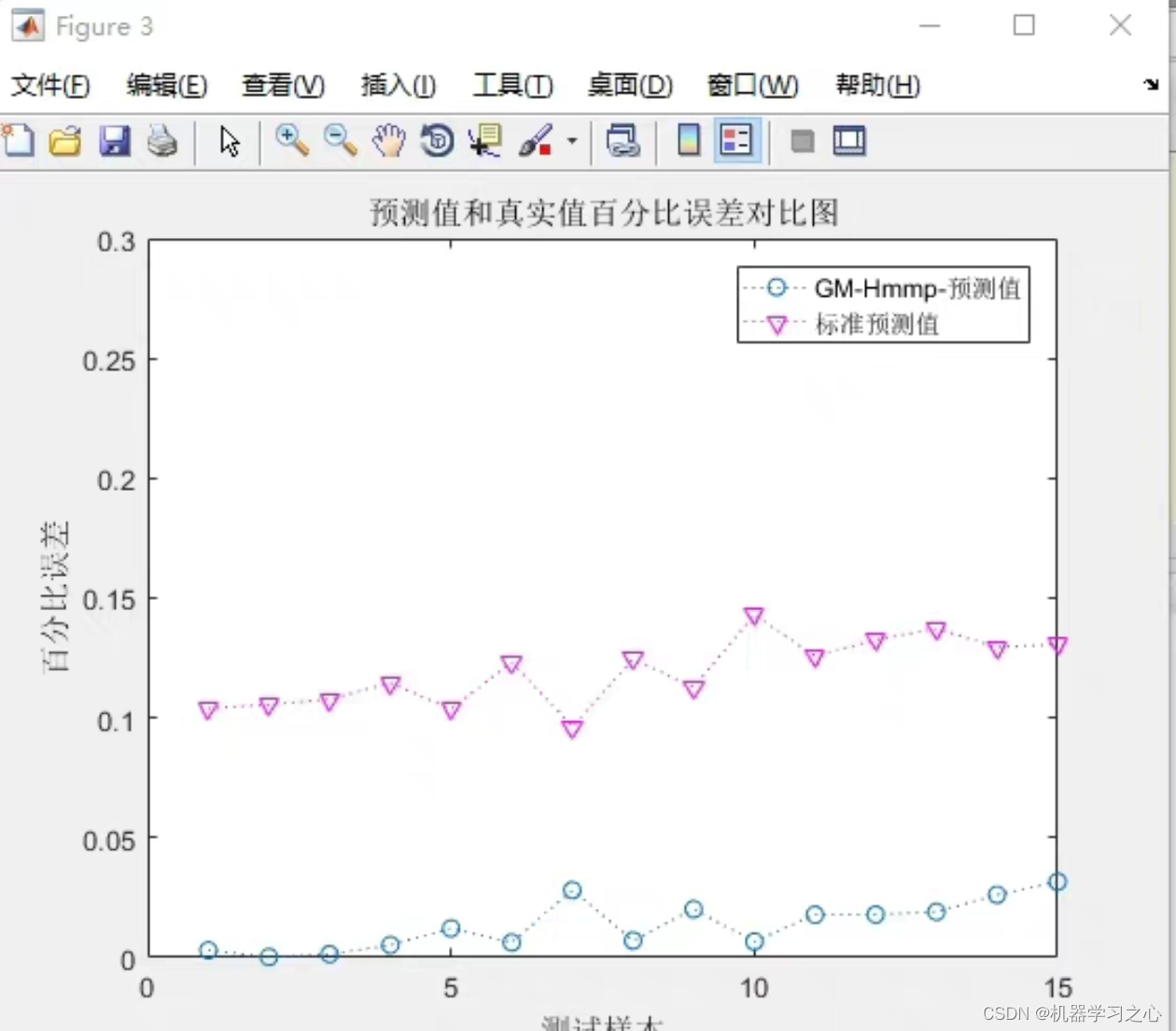
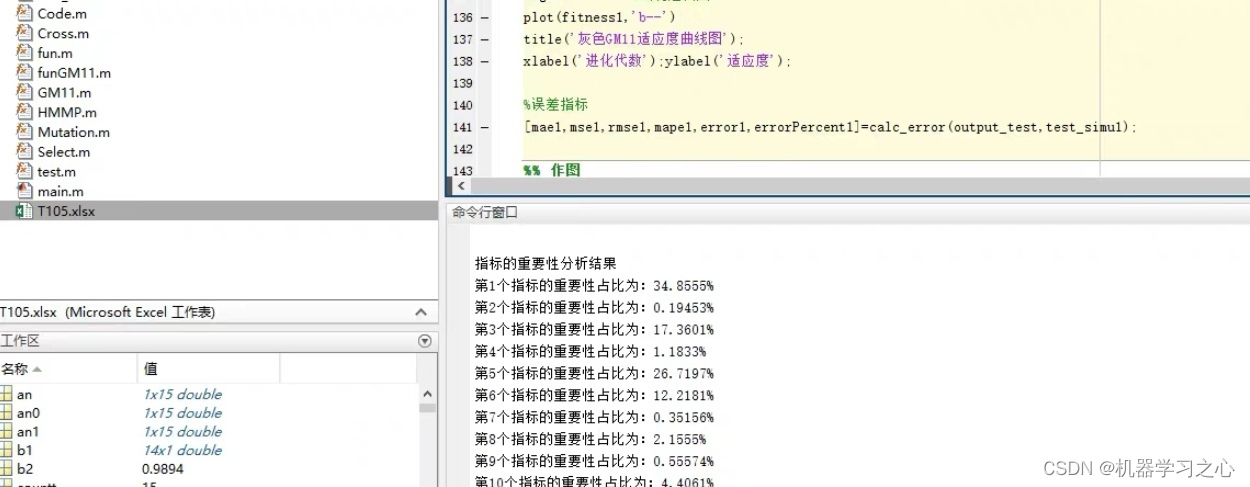
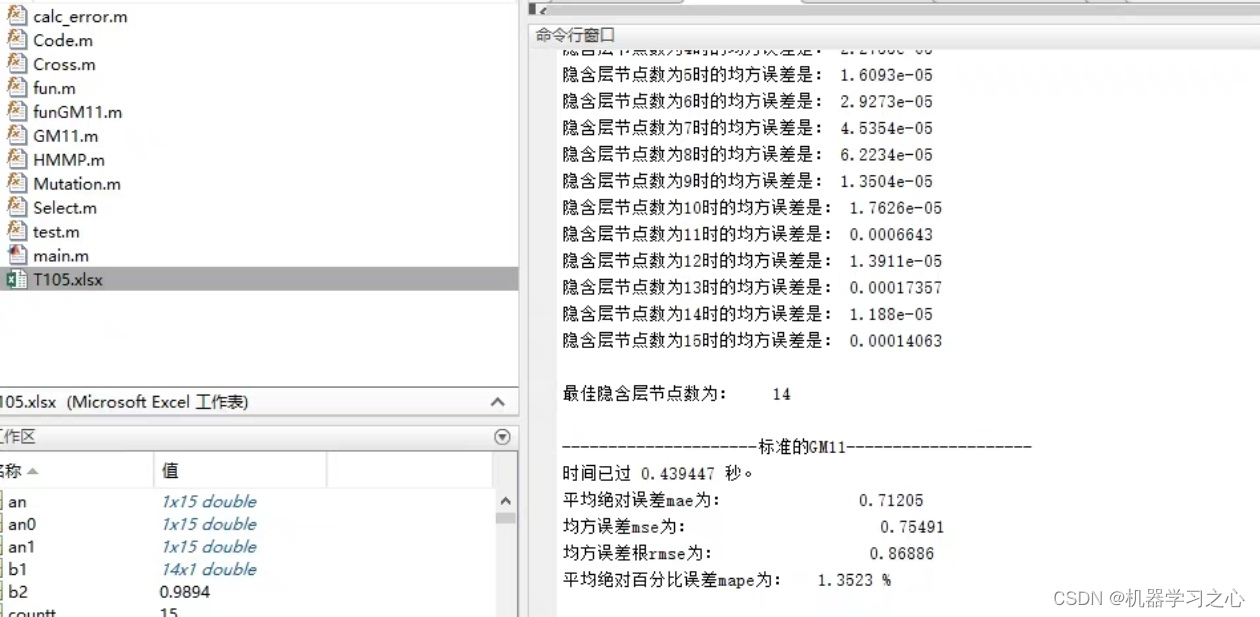
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

基本介绍

灰色HMMP-GM11改进模型,通过引入隐马尔可夫模型(HMM)来对原始数据进行状态分析，然后利用GM(1,1)模型进行预测，从而提高了预测精度。并采用变量筛选MIV方法对变量进行筛选，对每个指标的重要性进行分析。内附具体流程步骤

程序设计

  • 完整源码和数据下载地址私信回复Matlab基于灰色隐马尔可夫模型(HMMP-GM11)的时间序列预测。
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行



%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1', ps_output);
T_sim2 = mapminmax('reverse', t_sim2', ps_output);

%% V. 评价指标
%%  均方根误差 RMSE
error1 = sqrt(sum((T_sim1 - T_train).^2)./M);
error2 = sqrt(sum((T_test - T_sim2).^2)./N);

%% 决定系数
R1 = rsquare(T_train,T_sim1);
R2 = rsquare(T_test,T_sim2);

MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/124693040?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/124864369?spm=1001.2014.3001.5502

文章来源:https://blog.csdn.net/kjm13182345320/article/details/135488570
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。