Python - 深夜数据结构与算法之 Binary Search
目录
一.引言
前面介绍了二叉树和堆,其中涉及到有树和二叉搜索的概念,今天将二者整合介绍下常见的二分查找的问题。
二.二分查找的简介
1.查找条件

单调性 - 如果对应数据不具有单调性性质,则我们只能 o(n) 遍历寻找
上下界 - 存在上下界才能不断缩小范围
索引访问 - 列表可以,单链表的话不支持索引访问不容易二分
2.代码模版

right、left 即为我们的上下界,通过 mid 每次将搜索范围减半,时间复杂度为 log。代码模版中我们默认是升序排列的,如果是降序排序需要修改下elif 和 else 的逻辑,我们主要掌握上面的模版,即 left、rigth 的起始点,如何获取 mid 并判断。
3.查找示例

?数组满足有序、有界、索引访问所以可以进行二分查找,不断寻找 mid 缩小 left、right 的范围,就像高数里求数学极限的夹逼准则一样,直到找到 target 或者退出。
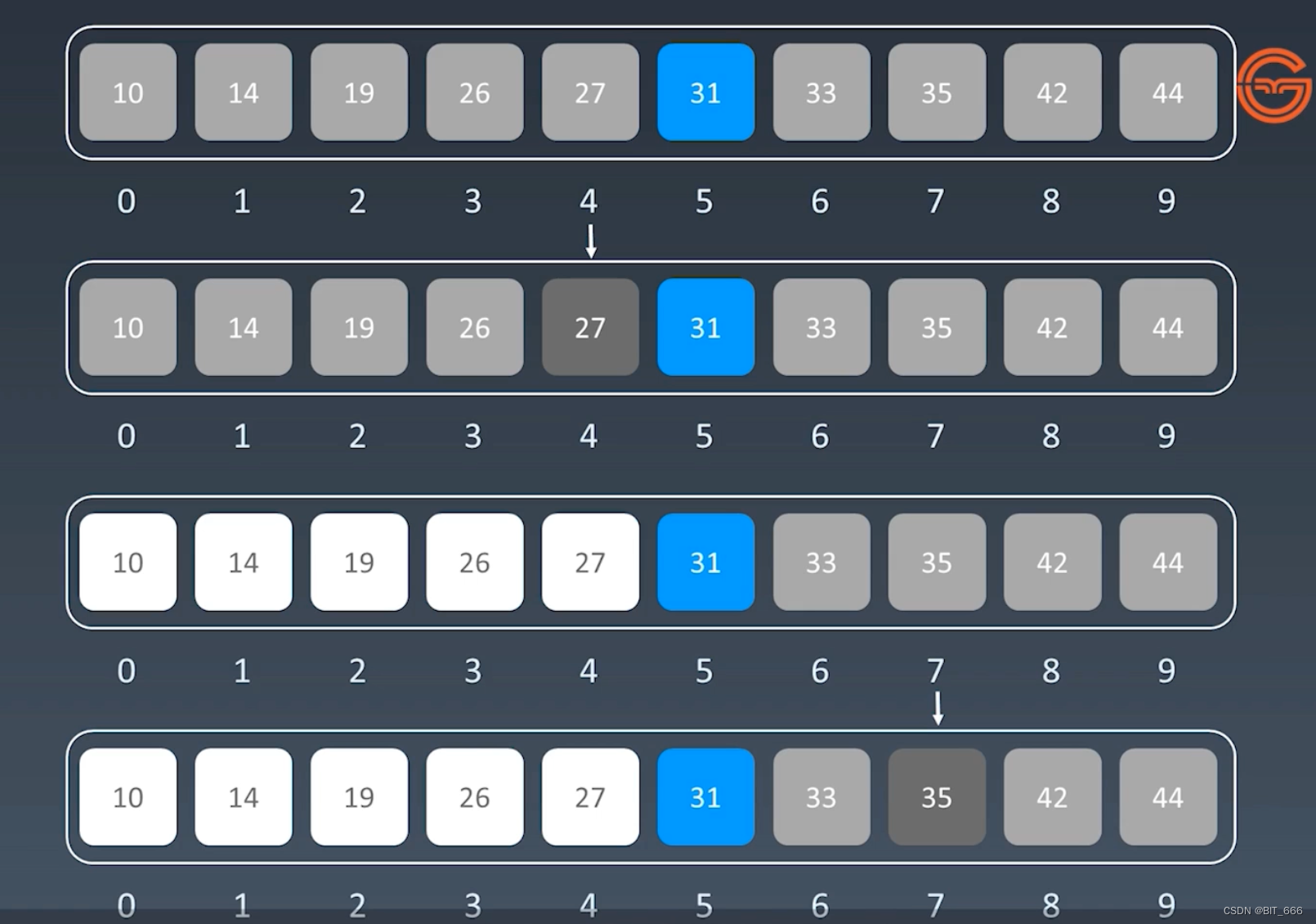
三.经典算法实战
1.Search-Rotated-List?[33]
搜索旋转排序数组:?https://leetcode.cn/problems/search-in-rotated-sorted-array

◆ 题目分析
对一个旋转后的有序数组进行排序,最暴力的方法无非 o(n) 遍历,找到突变的 index,即前后元素不保序,随后将数组恢复为有序再 sort,这个方法是最基础的,不过这里也可以套用二分查找的模版,只不过判断的边界条件会复杂一些,下面尝试下。
◆ 二分查找
class Solution(object):
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
# 找到了
if nums[mid] == target:
return mid
if nums[0] <= nums[mid]: # 左边数组有序 [4,5,6,7,0,1,2]
if nums[0] <= target < nums[mid]:
right = mid - 1
else:
left = mid + 1
else: # 右边数组有序 [6,7,0,1,2,4,5]
if nums[mid] < target <= nums[len(nums) - 1]:
left = mid + 1
else:
right = mid - 1
return -1这个题要求给出 log(n) 的解法,所以暴力求解是不行的,考虑使用二分查找主要需要明确一个点就是不管数组怎么分,它的左右两边一定是有一边有序的,我们只需要每次二分找有序的那一部分判断 target 在不在即可,不在就去另一边再找。因为 nums[mid] != target,所以两个有序区间都是一开一闭,左边为 '[)' 右边为 '(]'。

2.Sqrt-X [69]
X 的平方根:?https://leetcode.cn/problems/sqrtx/description/

◆ 题目分析
此题可以使用二分,我们看下三要素是否满足:?
- 单调性? x^2 函数是单调的
- 有界 对于 x 的平方根而言,其一定在 0-x 之间,有界
- 索引 这个这里不需要了,我们使用 o(1) 的内存就解决了
◆?二分查找
class Solution(object):
def mySqrt(self, x):
"""
:type x: int
:rtype: int
"""
# 左右界
left, right = 0, x
while left <= right:
# 取整
mid = (left + right) // 2
if x >= mid * mid:
left = mid + 1
else:
right = mid - 1
return right如果平方根 re^2 = x,则其整数部分一定满足 x >= int(re)^2。再解释下最后为什么返回 right,这里其实返回 left - 1 也一样,这是因为我们的 x 的平方根一定满足:
?re^2 <= x < (re+1)^2
当我们最后一次计算到 mid = (re+1)?时,此时进入 else 逻辑,left = re + 1,right = re,再次计算已经不满足 left <= right 的逻辑了,此时返回 right 或者 left - 1 都是返回 re。

3.Search-2D-Matrix [74]
搜索二维矩阵:?https://leetcode.cn/problems/search-a-2d-matrix

◆ 题目分析
给定从左到右递增的二维矩阵,求目标 target 是否存在,这题第一反应我们可以直接将 Matrix Flatten 打平为 1D 的 Array 再执行二分查找即可,还有一种就是分别在列和行上做二分查找,先找到对应行,再找到对应列里是否存在。
◆ 暴力二分查找
class Solution(object):
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
# 各种边界条件
if not matrix:
return False
if target < matrix[0][0] or target > matrix[len(matrix) - 1][len(matrix[0]) - 1]:
return False
nums = []
[nums.extend(i) for i in matrix]
# 寻找对应行
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return True
if nums[mid] > target:
right = mid - 1
else:
left = mid + 1
return False先 extend 再二分查找,这样遍历的是 o(mxn),如果只遍历行与列,则是 o(m + n)。

?
◆ 精简二分查找
class Solution(object):
def searchMatrix(self, matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
# 各种边界条件
if not matrix:
return False
if target < matrix[0][0] or target > matrix[len(matrix) - 1][len(matrix[0]) - 1]:
return False
# 寻找对应行
col_nums = [row[0] for row in matrix]
left, right = 0, len(col_nums) - 1
while left <= right:
mid = (left + right) // 2
if col_nums[mid] == target:
return True
if col_nums[mid] > target:
right = mid - 1
else:
left = mid + 1
# 在对应行操作
row_nums = matrix[right]
left, right = 0, len(row_nums) - 1
while left <= right:
mid = (left + right) // 2
if row_nums[mid] == target:
return True
if row_nums[mid] > target:
right = mid - 1
else:
left = mid + 1
return False
先找 col_nums 找到 target 应该在哪一行,再找 target 在不在 row_nums 里。

4.Find-Rotated-Min [153]
旋转排序最小值:?https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array

◆ 题目分析
二分查找的本质其实是通过条件缩小每次的检查范围,本题的思路直接想比较麻烦,在记事本上写一下会方便很多,这里我们二分的条件就是找小的在哪,无非左边或右边,所以我们直接列举全部情况即可。
◆ 二分查找
class Solution(object):
def findMin(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# 完全有序
if nums[0] <= nums[-1]:
return nums[0]
left, right = 0, len(nums) - 1
# 找哪边小,去小的那边接着找
while left <= right:
if nums[left] == nums[right]:
return nums[left]
mid = (left + right) // 2
# [2, 3, 4, 5, 1] 中间比左边大 -> 右边
if nums[mid] >= nums[0]:
left = mid + 1
# [5, 1, 2, 3, 4] 中间比左边小 -> 左边
else:
right = mid
return nums[left]
nums[0] <= nums[-1]? 完全有序,直接出第一个最小的
nums[mid] >= nums[0] 左边有序,最小值在右边 left = mid + 1
nums[mid] < nums[0] 最小值在左边,结合在中间的特殊情况 right = mid
5.Valid-Perfect-Square [367]
有效的完全平方数:?https://leetcode-cn.com/problems/valid-perfect-square/

◆ 题目分析
找平方的题目,起始就是找到 re ^^ 2 <= num < (re+1) ^^ 2,此时 left = re+1,right = re,因为我们判断是否是完全平方,所以判断 re ^^ 2 == num 即可。
◆ 二分查找?
class Solution(object):
def isPerfectSquare(self, num):
"""
:type num: int
:rtype: bool
"""
left, right = 0, num
while left <= right:
mid = (left + right) // 2
if num >= mid * mid:
left = mid + 1
else:
right = mid - 1
return right ** 2 == num直接看是否是 int(re) 的平方即可。

?
四.总结
二分查找的核心思路是根据优先级关系进行搜索区间的缩小,由于其主要就向左和向右两种情况,很多时候没思路可以直接在纸上把几种情况罗列一下再分析,会更容易上手一些。至于一些 < 还是 <=,+1 还是 -1 可以多调试几次,最后理解含义。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
