打家劫舍总结

近期刷了几道打家劫舍的题,趁还没忘赶紧把复盘写一下

leetcode 198 打家劫舍

这个是我们的原型题,其他的题目都是在这个题目的基础上延展开来的

题目就是说有一堆房屋,每个房屋都有一定的金钱数,我们不能偷相邻的房屋,求能获得的最大金额

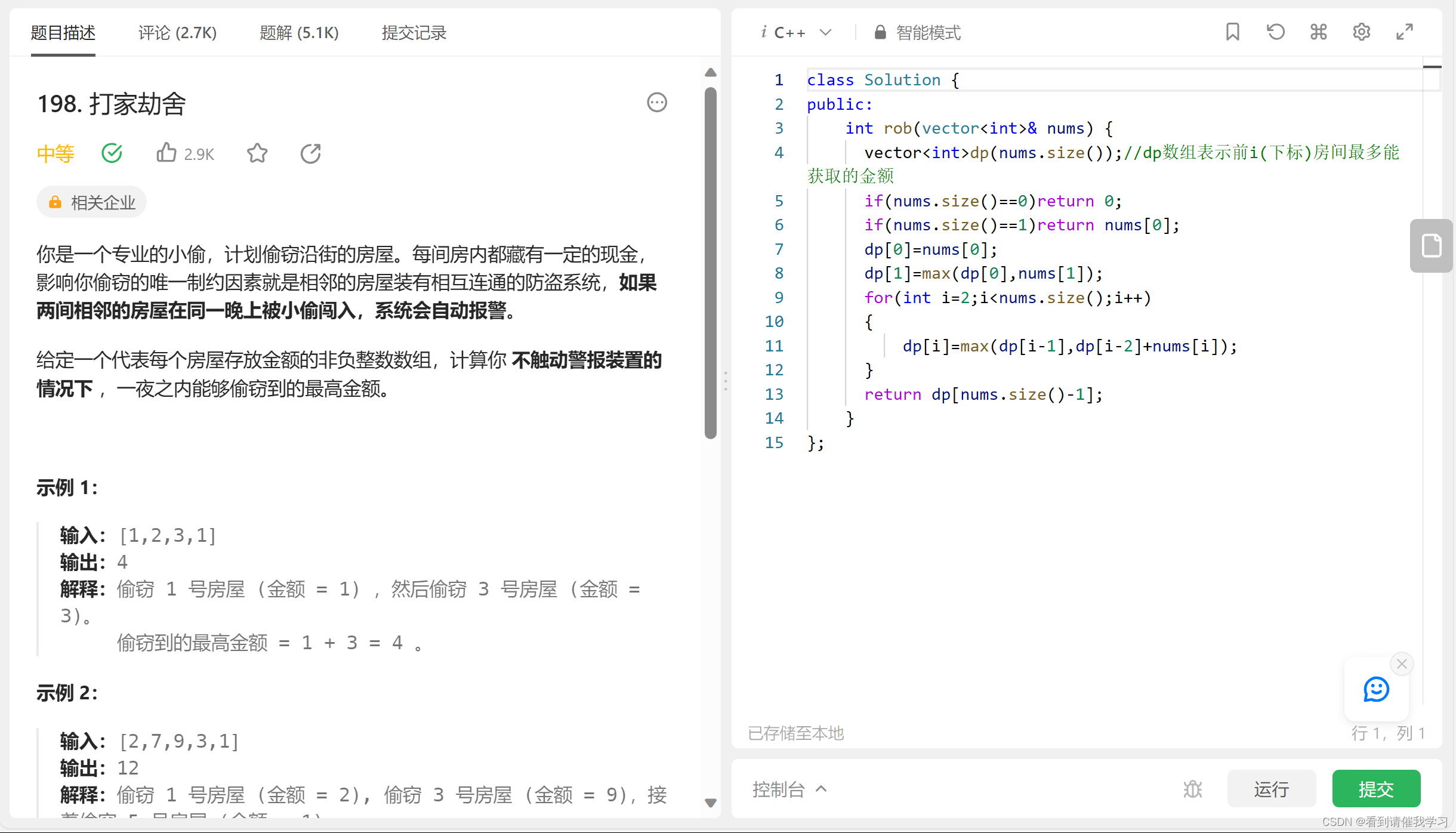
首先第一个坑就是分清楚问题是贪心还是动规,有些同学做着做着很容易就把他当成了贪心,实际上并不是这样的,我们可以从一号房间出发(下标0)也可以从二号房间(下标1)出发,两种情况选出最大者而不是单纯的局部最优,就像上图的示例一一样,局部最优(2)不一定得到的是全局最优的结果

明确了问题类型是dp之后就好办了,使用我们的动规三部曲:定义,初始化,遍历

题目要求最高金额,我们就设dp的意义为经过i个房间之后能获取的最大金额,初始化我们的dp[0],dp[1],为什么这样初始化应该很好理解,接下来就是我们的递推公式,因为我们可以选择偷与不偷(这和背包问题放和不放是一样的),当我们不偷的时候dp的值(dp[i])和他前一个值(dp[i-1])相同,偷的时候因为不能取相邻,因此我们只能取前面的前面的值(dp[i-2]),因此打家劫舍的递推公式为dp[i]=max(dp[i-1],dp[i-2]+nums[i]),剩下的步骤就不说了

leetcode 213 打家劫舍2?

是上一题的进阶版,多了一个要求就是第一个和最后一个不能同时取

在讲解法之前,先讲一个坑:根据奇偶性进行分类讨论,我一开始看了例子之后就掉进这个坑里了,其实根本不需要分类,奇偶性并不影响结果,出现这个问题的原因还是对打家劫舍的本质不够了解

我们知道第一个和最后一个不能同时取,这和我们原题中第一个和第二个不能同时取很相似,我们只需要两者二选一即可,分成0~nums.size()-2,1~nums.size()-1两种类型,分别把第一个和最后一个元素排除出去,剩下的元素按照原题的方法来做即可

leetcode 337 打家劫舍3

dp问题延伸到树上面,也就成了我们的树形dp问题

看到这道题我一开始的想法就是层序遍历+原型dp,看似很有道理的感觉

但是直到我看到这种情况的时候:

3和4不是同一层,但是因为不是同父节点所以可以取,说明我层序遍历的想法是错的,正确的做法应该是用后序遍历,将值从底层一层层往上传,一般这种树结构要计算值的题目都是用的后序遍历,没想到说明对树的那部分知识有点忘了

这里我觉得比较好理解的方法是记忆化递推,用一个哈希表记录已经计算过的对象,这样可以避免重复计算导致的超时

抓住打家劫舍问题的本质:偷还是不偷,偷就不能取当前节点的孩子,不偷就取当前节点的孩子

unordered_map<TreeNode*,int>nums;
    public:
    int rob(TreeNode*root){
        return tryrob(root);
    }
    int tryrob(TreeNode*node)
    {
        if(!node)return 0;
        if(nums.count(node))return nums[node];
        //偷该节点
        int num1=0;
        num1+=node->val;
        if(node->left){
            num1+=tryrob(node->left->left)+tryrob(node->left->right);
        }
        if(node->right){
            num1+=tryrob(node->right->left)+tryrob(node->right->right);
        }
        //不偷该节点
        int num2=0;
        num2=tryrob(node->left)+tryrob(node->right);
        nums[node]=max(num1,num2);
        return nums[node];
    }

我们不要从根节点的角度看,要从最底层节点的角度看,我们一层一层的把值传递上去,也就是进行后序遍历,我们的问题是这个节点要偷吗,不偷的话我们应该把那些值传上去?

偷,我们就把当前这个节点的加进值里面,并把这个节点的孩子的孩子的值加上(如果节点的孩子存在),不偷我们就把当前节点的孩子加上,两者取最大值往上面送,当作当前节点的值(可以理解为dp[i])

那么最后tryrob(root)就是根节点的值dp[root]

动规的写法可以参照卡哥的题解