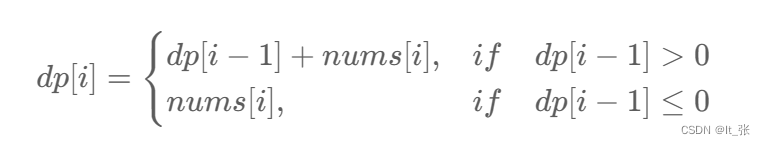Java算法练习2

12.11 反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。

示例 1：

输入：s = ["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：s = ["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

//利用双指针一个指向数组开始一个指向数组结尾
class Solution {
    public void reverseString(char[] s) {
        for(int i = 0,j = s.length - 1;i < j;i++,j--){
            char c = ' ';
            c = s[i];
            s[i] = s[j];
            s[j] = c;
        }
    }
}

12.12 斐波那契数

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

//法一 利用斐波那契性质，本数字等于前两个数字之和
class Solution {
    public int fib(int n) {
        if(n < 2){
            return n;
        }
        int a = 0,b = 0,c = 1;
        for(int i = 2;i <= n;i++){
            a = b;
            b = c;
            c = a + b;
        }
        return c;
    }
} 
//法二 递归
class Solution {
    public int fib(int n) {
        if(n==0) return 0;
        if(n==1) return 1;
        return fib(n-1) + fib(n-2);
    }
}

12.13 最长的斐波那契子序列的长度

如果序列 X_1, X_2, ..., X_n 满足下列条件，就说它是 斐波那契式 的：

• n >= 3
• 对于所有 i + 2 <= n，都有 X_i + X_{i+1} = X_{i+2}

给定一个严格递增的正整数数组形成序列 arr ，找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在，返回 0 。

（回想一下，子序列是从原序列 arr 中派生出来的，它从 arr 中删掉任意数量的元素（也可以不删），而不改变其余元素的顺序。例如， [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列）

示例 1：

输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。

示例 2：

输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18] 。

//暴力
class Solution {
    public int lenLongestFibSubseq(int[] arr) {
       int num = 2;
        int endNum = 0;
        for(int i = 0;i < arr.length;i++){
        	 int sum = 0;
             for(int k = i + 1;k < arr.length;k++){
                sum = arr[i] + arr[k];
                // System.out.print(arr[i]+" "+ arr[k]);
                endNum = Math.max(endNum,num);
                num = 2;
                int arrk = arr[k];
                for(int j = k + 1;j < arr.length ;j++){
                	if(arr[j] > sum) break;
                    if(arr[j] == sum){
                    	// System.out.print(" " + arr[j]);
                        num++;
                        sum = arrk + arr[j];
                        arrk = arr[j];
                    } 
                }
                // System.out.println();
             }
            
        }
        return endNum==2?0:endNum;
    }
}

//动态规划
class Solution {
    public int lenLongestFibSubseq(int[] arr) {
        //使用map集合来存储数组元素以便于更快的找到值所对应的下标
        Map<Integer, Integer> indices = new HashMap<Integer, Integer>();
        int n = arr.length;
        for (int i = 0; i < n; i++) {
             //这里将数组arr元素的值当作键
            indices.put(arr[i], i);
        }
        //二维数组dp用来存放以数j和数i结尾的数列长度
        int[][] dp = new int[n][n]; 
        int ans = 0;
        //arr[k] +  arr[j] = arr[i]
        //来寻找arr[i]这个数
        for (int i = 2; i < n; i++) { 
            //从i这个位置依次往前找，arr[j] * 2 > arr[i]：因为arr[j] 之前的数arr[k]一定比arr[j]小,
            //所以两个arr[j]不能等于arr[i]时，arr[k] + arr[j] 一定不会等于arr[i]
            for (int j = i - 1; j >= 0 && arr[j] * 2 > arr[i]; j--) { 
                //从集合indices中获取arr[k]值是否存在如果存在则输出它的下标，不存在则输出-1
                int k = indices.getOrDefault(arr[i] - arr[j], -1); 
                if (k >= 0) {
                    存在时则直接就赋值，因为数组dp初始值为0，所以要判断
                    dp[j][i] = Math.max(dp[k][j] + 1, 3); 
                }
                ans = Math.max(ans, dp[j][i]);
            }
        }
        return ans;
    }
}

12.14 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

//法一 其实就是斐波那契数列用递归
class Solution {
    public int climbStairs(int n) {
        if(n == 2) return 2;
        if(n == 1) return 1;
        return climbStairs(n-1) + climbStairs(n-2);
    }
}

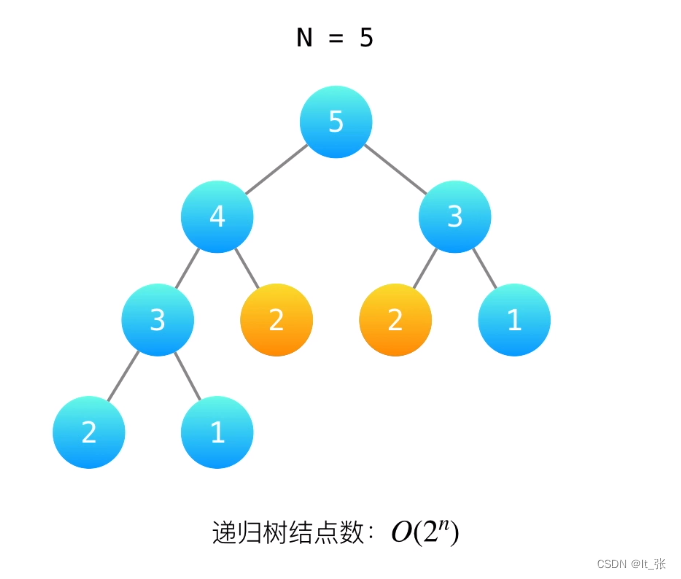
//法二 利用动态规划为什么要用动态规划呢？
//解答在上面利用斐波那契数列时会有重复计算的现象如上图
class Solution {
    public int climbStairs(int n) {
        if(n == 1) return 1;
        int[] arr = new int[n+1];
        arr[1] = 1;
        arr[2] = 2;
        for(int i = 3;i <= n;i++){
            arr[i] = arr[i-1] + arr[i-2];
        }
        return arr[n];
    }
}

//法三 滚动数组思想
//在上面动态规划思想上发现第i项只与第i-1和第i-2项有关
//所以可以将空间复杂度降低为O(1)
class Solution {
    public int climbStairs(int n) {
        int a  = 1, b = 2,c = 0;
        for(int i = 3;i <= n;i++){
            c = a + b;
            a = b;
            b = c;
        }
        return n <= 2 ? n : c;
    }
}

12.15 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

解题思路： 点击详解

1.定义状态（定义子问题）：dp[i]：表示以 nums[i] 结尾 的 连续 子数组的最大和。

2.状态转移方程（描述子问题之间的联系）：如果 dp[i - 1] > 0，那么可以把 nums[i] 直接接在 dp[i - 1] 表示的那个数组的后面，得到和更大的连续子数组；如果dp[i - 1] < 0，那么 nums[i]加上前面的数 dp[i - 1] 以后值不会变大。此时单独的一个 nums[i] 的值，就是 dp[i]

//法一
class Solution {
   public static int maxSubArray(int[] nums) {
        int n =  nums.length;
        int[] dp = new int[n];
        dp[0] = nums[0];
        int num = dp[0];
        for(int i = 1;i < n;i++){
            if(dp[i-1] > 0){
                dp[i] = dp[i-1] + nums[i];
            }else{
                dp[i] = nums[i];   
            }
            num = Math.max(dp[i],num);
        }
        return num;
   }
}

空间优化后的代码

//法二
class Solution {
   public static int maxSubArray(int[] nums) {
        int n =  nums.length;
        int num = nums[0];
        for(int i = 1;i < n;i++){
            if(nums[i-1] > 0){
                nums[i] = nums[i-1] + nums[i];
            }else{
                nums[i] = nums[i];   
            }
            num = Math.max(nums[i],num);
        }
        return num;
   }
}