Rust逆向学习 (7)
文章目录
Reverse for HashMap
HashMap是各个语言常用的一种数据结构,在每个语言中的实现都有或多或少的差别,相信学过数据结构的都知道HashMap在数据量较大时具有很小的时间复杂度。下面我们将分析在Rust中,HashMap在内存中的表示方式。
new / insert / get
use std::collections::HashMap;
pub fn main(){
let mut map: HashMap<u64, u64> = HashMap::new();
map.insert(1, 2);
println!("{}", map.get(&1u64).unwrap());
}
以上面的代码为例。我们分段看一下对应的汇编代码:
example::main:
sub rsp, 200
mov rax, qword ptr [rip + std::collections::hash::map::HashMap<K,V>::new@GOTPCREL]
lea rdi, [rsp + 48]
mov qword ptr [rsp + 40], rdi
call rax
mov rdi, qword ptr [rsp + 40]
mov rax, qword ptr [rip + std::collections::hash::map::HashMap<K,V,S>::insert@GOTPCREL]
mov esi, 1
mov edx, 2
call rax
jmp .LBB157_3
上面的代码包含了new和insert两个操作,通过调试发现,new方法与字符串、可变数组的new类似,都是传入要初始化的栈指针。在初始化完成之后,这部分栈的数据如下所示,貌似看不出来什么特殊的地方。
pwndbg> tele 0x7fffffffd910
00:0000│ rax rdi 0x7fffffffd910 —? 0x5555555a62d0 ?— 0xffffffffffffffff
01:0008│ 0x7fffffffd918 ?— 0x0
... ↓ 2 skipped
04:0020│ 0x7fffffffd930 ?— 0x419fa2b4be855595
05:0028│ 0x7fffffffd938 ?— 0x944210c733652a9b
往下是插入方法的调用,参数类型也很明显,第一个为HashMap栈指针,第二个是Key,第三个是Value。我们要重点看一下调用后HashMap的内存结构长啥样。
pwndbg> tele 0x7fffffffd910
00:0000│ 0x7fffffffd910 —? 0x5555555bebe0 ?— 0xffffffffff45ffff
01:0008│ 0x7fffffffd918 ?— 0x3
02:0010│ 0x7fffffffd920 ?— 0x2
03:0018│ 0x7fffffffd928 ?— 0x1
04:0020│ 0x7fffffffd930 ?— 0x419fa2b4be855595
05:0028│ 0x7fffffffd938 ?— 0x944210c733652a9b
pwndbg> tele 0x5555555beb90
00:0000│ 0x5555555beb90 ?— 0x0
01:0008│ 0x5555555beb98 ?— 0x61 /* 'a' */
02:0010│ r9 0x5555555beba0 ?— 0x0
03:0018│ 0x5555555beba8 ?— 0x0
04:0020│ rcx 0x5555555bebb0 ?— 0x1
05:0028│ 0x5555555bebb8 ?— 0x2
06:0030│ 0x5555555bebc0 ?— 0x0
07:0038│ 0x5555555bebc8 ?— 0x0
pwndbg>
08:0040│ 0x5555555bebd0 ?— 0x0
09:0048│ 0x5555555bebd8 ?— 0x0
0a:0050│ rdi 0x5555555bebe0 ?— 0xffffffffff45ffff
0b:0058│ 0x5555555bebe8 ?— 0xffffffffffffffff
0c:0060│ 0x5555555bebf0 ?— 0xff45ffff
0d:0068│ 0x5555555bebf8 ?— 0x20411
0e:0070│ 0x5555555bec00 ?— 0x0
0f:0078│ 0x5555555bec08 ?— 0x0
可以看到,0x5555555beb90应该就是与HashMap相关的数据结构,下面的0x20411是top chunk的大小,后面的内容不属于这个chunk。值得注意的是,这个chunk中确实保存了我们插入的数据,后面还有一些由0xFF组成的未知数据结构。这样看来,单插入一个数据看不出来它的具体实现方式,因此这里尝试多插入一些结构,看看内存的变化。
不看不知道,一看发现,其中的玄机还挺大。在HashMap的栈对象内存空间中,我们在最后可以看到有一个被像是随机数一类的数据占用的0x10大小的内存空间,从IDA反编译可以得知,这是std::collection::hash_map::RandomState实例。这又是一个什么东西呢?
pub struct RandomState {
k0: u64,
k1: u64,
}
impl RandomState {
#[inline]
#[allow(deprecated)]
#[must_use]
#[stable(feature = "hashmap_build_hasher", since = "1.7.0")]
pub fn new() -> RandomState {
thread_local!(static KEYS: Cell<(u64, u64)> = {
Cell::new(sys::hashmap_random_keys())
});
KEYS.with(|keys| {
let (k0, k1) = keys.get();
keys.set((k0.wrapping_add(1), k1));
RandomState { k0, k1 }
})
}
}
从上面的Rust内核部分源码可以看到,这里保存的确实是两个随机数,经过测试发现,两个随机数的值每一次执行都不一样。
那么,HashMap为什么需要这样一个结构呢?继续往下看源码:
#[stable(since = "1.7.0", feature = "build_hasher")]
pub trait BuildHasher {
#[stable(since = "1.7.0", feature = "build_hasher")]
type Hasher: Hasher;
#[stable(since = "1.7.0", feature = "build_hasher")]
fn build_hasher(&self) -> Self::Hasher;
#[stable(feature = "build_hasher_simple_hash_one", since = "1.71.0")]
fn hash_one<T: Hash>(&self, x: T) -> u64
where
Self: Sized,
Self::Hasher: Hasher,
{
let mut hasher = self.build_hasher();
x.hash(&mut hasher);
hasher.finish()
}
}
#[stable(feature = "hashmap_build_hasher", since = "1.7.0")]
impl BuildHasher for RandomState {
type Hasher = DefaultHasher;
#[inline]
#[allow(deprecated)]
fn build_hasher(&self) -> DefaultHasher {
DefaultHasher(SipHasher13::new_with_keys(self.k0, self.k1))
}
}
从RandomState对BuildHasher这个Trait进行impl的情况来看,HashMap使用的是SipHasher13这种Hash算法。这种算法多用于短消息的哈希,是一个伪随机函数族,可作为消息认证的MAC函数使用,具有安全、快速、简洁等特点。具体的算法参见传送门。HashMap在每一次insert与get的时候都会使用这个Hash函数进行计算。
好,现在我们知道HashMap使用什么哈希函数进行计算了,并且通过上面的分析也能够得出下面的结论:在一个Rust进程中,即使是泛型类型完全相同的两个HashMap结构,对于同一个Key所计算出的Hash值也几乎是不可能相同的,因为所使用的SipHasher算法的两个key值是随机生成的,对于不同的key值,计算出来的Hash值也不同。
分析出使用的Hash函数后,我们可以开始解决其他的问题了。第一:这些Hash值在什么地方保存?第二:之前在堆中看到的大部分是0xFF的那一堆数据到底有什么用?
首先解决第一个问题。在调试中通过检查内存情况发现,这些Hash值没有保存在栈或堆中。没有保存在栈好理解,毕竟一个HashMap可能有很多个Hash值,全保存在栈里很可能爆栈的。但是堆空间也没有找到就很有意思了。从IDA反汇编的结果来看,在insert和get内部还调用了其他的方法。在insert中:
pub fn insert(&mut self, k: K, v: V) -> Option<V> {
let hash = make_hash::<K, S>(&self.hash_builder, &k);
let hasher = make_hasher::<_, V, S>(&self.hash_builder);
match self
.table
.find_or_find_insert_slot(hash, equivalent_key(&k), hasher)
{
Ok(bucket) => Some(mem::replace(unsafe { &mut bucket.as_mut().1 }, v)),
Err(slot) => {
unsafe {
self.table.insert_in_slot(hash, slot, (k, v));
}
None
}
}
}
可以看到,这里使用hash值(不可变变量hash)的关键方法有find_or_find_insert_slot和insert_in_slot这两个。整个insert方法的逻辑和Rust中对于HashMap的插入操作逻辑相同——当Key存在时,使用新的Value替换旧的Value;当Key不存在时,将Key插入并添加Value。在上面的insert内核方法中,k即为新的Key,v即为新的Value。
#[inline]
pub fn find_or_find_insert_slot(
&mut self,
hash: u64,
mut eq: impl FnMut(&T) -> bool,
hasher: impl Fn(&T) -> u64,
) -> Result<Bucket<T>, InsertSlot> {
self.reserve(1, hasher);
unsafe {
match self
.table
.find_or_find_insert_slot_inner(hash, &mut |index| eq(self.bucket(index).as_ref()))
{
// SAFETY: See explanation above.
Ok(index) => Ok(self.bucket(index)),
Err(slot) => Err(slot),
}
}
}
#[inline]
unsafe fn find_or_find_insert_slot_inner(
&self,
hash: u64,
eq: &mut dyn FnMut(usize) -> bool,
) -> Result<usize, InsertSlot> {
let mut insert_slot = None;
let h2_hash = h2(hash);
let mut probe_seq = self.probe_seq(hash);
loop {
let group = unsafe { Group::load(self.ctrl(probe_seq.pos)) };
for bit in group.match_byte(h2_hash) {
let index = (probe_seq.pos + bit) & self.bucket_mask;
if likely(eq(index)) {
return Ok(index);
}
}
if likely(insert_slot.is_none()) {
insert_slot = self.find_insert_slot_in_group(&group, &probe_seq);
}
if likely(group.match_empty().any_bit_set()) {
unsafe {
return Err(self.fix_insert_slot(insert_slot.unwrap_unchecked()));
}
}
probe_seq.move_next(self.bucket_mask);
}
}
注意到了吗?上面的unsafe方法find_or_find_insert_slot_inner中有一个h2方法:
#[inline]
#[allow(clippy::cast_possible_truncation)]
fn h2(hash: u64) -> u8 {
// Grab the top 7 bits of the hash. While the hash is normally a full 64-bit
// value, some hash functions (such as FxHash) produce a usize result
// instead, which means that the top 32 bits are 0 on 32-bit platforms.
// So we use MIN_HASH_LEN constant to handle this.
let top7 = hash >> (MIN_HASH_LEN * 8 - 7);
(top7 & 0x7f) as u8 // truncation
}
破案了,这里获取了hash的最高7位,经过调试证实,堆空间中一串0xFF中间掺杂的其他数据就是这些Hash值的最高7位。通过这个方法名,实际上已经可以在网上找到这个HashMap的算法了——Swiss Tables。经过简单了解后发现,它与Rust中的实现高度吻合。这是一种较新的高效HashMap算法,需要保存Key和Value本身,通过若干个16字节大小的桶进行索引。具体的算法实现可见传送门,下面也将进行简单介绍。
Swiss Tables
Data Structure
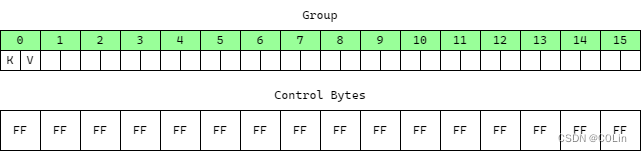
这个算法包含两个最为重要的数据结构,第一是若干个Group,每一个Group都是一个长度固定为16的数组,所有元素均为键值对,这里称每一个数组项为桶(Bucket)。第二是控制字节(Control Bytes)数组,对于每一个Group中的每一个元素,都有一个1字节的控制字节,因此控制字节数组的字节数量等于Group数量乘以16。
在这个算法中,需要对Hash进行如下操作:将Hash值截为无符号64位值(Rust中如果使用默认Hash算法,其输出就是无符号64位值,因此无需截断),随后分为最高7位与余下的57位。最高7位将被用来填充保存该元素的桶的控制字节的低7位,最高1位另有作用。余下的57位将用于确定将这个值保存在哪个Group中。在Rust中,控制字节为全1代表这个桶为空,为128代表这个桶被删除。
为方便说明,下面的所有图中,以绿色代表桶空,黄色代表满,红色代表已删除。
Insert/Delete/Find
那么这里就出现了一个问题:如果57位只是用来确定应该保存在哪个组,那么应该如何确定保存到组中的哪个桶呢?实际上这个问题根本不需要考虑,因为Swiss Tables充分考虑了现代CPU浮点数架构的性能优化,对于一个组,它的控制字节一共16字节,正好是一个浮点寄存器的大小,在实际实现的时候可以通过使用浮点数指令来进行加速,无论元素被保存到一个组中的哪个桶,都能够在固定的时间完成对一组的查找下面通过查找来简单说明。
如果需要查找某个Key,首先计算Hash值,随后获取高7位与其应该保存到的组的索引值,为方便说明,假设高7位为0x18。下面首先要完成的工作是尝试匹配高7字节,即在这个桶的16字节中尝试找到一个字节的值为0x18。找到之后还需要进一步比较Key值是否真的相等,因为7字节的空间很小容易发生碰撞。如果没有匹配到,需要判断这个组是否已经填满。因为Swiss Tables的插入规则中包含这样一条:当目标组已满时,需要判断该组的下一个组是否全满,如果不是则保存到下一个组,如果是则继续向下查找。也就是说,在查找的时候如果发现目标组已经填满且组中没有找到Key,则还需要向下查找下面的组,直到查找到Key或检测到某个组不是全满为止。
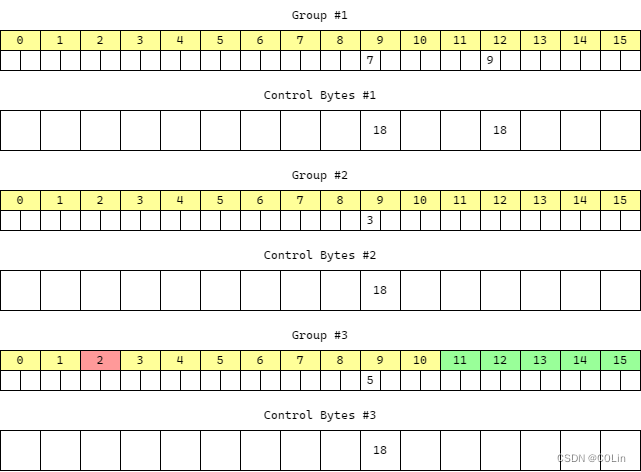
以上图为例,如果现在需要查找3这个Key,Hash高7位为0x18,计算出的Hash值表示它应该被保存到组1中。但在插入时由于组1已满,因此被插入到组2中。在查找时,可首先通过一条浮点数指令将1个字节的值复制到16个字节的浮点数寄存器中,使浮点数寄存器的16个字节的值都等于0x18,随后使用两条浮点数指令将16个控制字节与浮点数寄存器进行逐字节比较获取16字节输出,相同的字节在输出中对应为值1,不同为0。最后获取到所有控制字节匹配的桶,进行Key的比较。
在上图的例子中,对组1进行匹配时发现没有找到3,且注意到这个组全满,因此需要继续匹配下面一组,在下面一组中找到了3这个Key,查找完成,Hit。
如果要查找6这个Key,且它的Hash值高7位也是0x18,那么在查找到组2没有找到后,还需要查找组3,组3中也没有,但组3不是全满,因此判断HashMap中不存在6这个Key,Miss。
从上面的分析可以看出,Swiss Tables在插入时遵循线性探测规则。根据上面所述的规则,我们能够基本完成对HashMap的插入、删除与查询操作。
不过上面的查找算法还有一个问题需要解决:对于已经删除的项,是应该将其视作满还是空?考虑一下:如果将删除项视作空,那么对于一堆全满的连续的多个组,在每个组中都可能保存有原本应该保存在这一堆中第一个组的元素,却因为前面的组都满了而被赶到了后面保存,将其视作空就相当于是减少了连续的全满的组的数量,假设有原本应该保存在组1的元素a被保存到组4,而组3删除了一个元素,那么在查找a的时候,只是找到组3就会退出,这样显然是错误的。因此查找时,对于已删除元素,应将其看做桶满。
Expand
下面,我们还需要解决这个算法中的一个重要部分:扩容。如果所有组中空闲桶数量不足需要扩充,扩充前后同一个元素的Hash值计算出来应该保存到的组的索引有可能不同,这样原本应该保存到同一个组的元素可能会保存到相距很远的不同组中。举例说明,如果后57位确定组是通过将值对组数取模得到,那么对于一个原来有4组的HashMap,将其扩充到8组后,Hash值为0x5的数据在扩容前应该被保存到组1,但扩容后则会被保存到组5。扩容后若进行查找,也是从组5开始查找,此时无法查找到组1的这个数据。这个问题如何解决?如果组的数量没有即使扩充,当产生的连续全满组数量较多时,有可能会导致一次查找需要遍历所有这些全满组,导致效率有所降低,这个问题如何解决?
千言万语都说明,我们需要一个正确的高效的扩容算法。但很可惜的是,扩容算法的解释在网络中几乎没有,针对Swiss Tables的介绍大多是针对前面三种操作以及分析其查询效率为什么高。那么下面,我们将通过实际的试验验证Rust中HashMap的扩容策略。
首先,我们需要明确Rust HashMap在什么时候扩容。通过查看Rust源码发现了这样一个方法:
fn bucket_mask_to_capacity(bucket_mask: usize) -> usize {
if bucket_mask < 8 {
// For tables with 1/2/4/8 buckets, we always reserve one empty slot.
// Keep in mind that the bucket mask is one less than the bucket count.
bucket_mask
} else {
// For larger tables we reserve 12.5% of the slots as empty.
((bucket_mask + 1) / 8) * 7
}
}
从注释中可以看出,对于桶数量为1/2/4/8的HashMap,Rust总是保留一个空的桶,而更大的HashMap则保留1/8的桶为空。这一点可以通过反复调用HashMap的capacity方法找到端倪。当我们一个个插入数据的时候,输出的capacity去重后是这样一个序列:3, 7, 14(16x7÷8), 28(32x7÷8), 56(64x7÷8), …。
接下来,这里重点探究一下Rust HashMap在扩容前后数据位置的变化情况。笔者本来是想通过直接搜索源码查找相关代码的,但找了半天无功而返,因此只得寻求动态调试的帮助。结果很简单就找到了,但是不知道为什么,调试显示的行与实际行不同。下面找到了一个resize,但是看不懂:
unsafe fn resize(
&mut self,
capacity: usize,
hasher: impl Fn(&T) -> u64,
fallibility: Fallibility,
) -> Result<(), TryReserveError> {
// SAFETY:
// 1. The caller of this function guarantees that `capacity >= self.table.items`.
// 2. We know for sure that `alloc` and `layout` matches the [`Allocator`] and
// [`TableLayout`] that were used to allocate this table.
// 3. The caller ensures that the control bytes of the `RawTableInner`
// are already initialized.
self.table.resize_inner(
&self.alloc,
capacity,
&|table, index| hasher(table.bucket::<T>(index).as_ref()),
fallibility,
Self::TABLE_LAYOUT,
)
}
#[allow(clippy::inline_always)]
#[inline(always)]
unsafe fn resize_inner<A>(
&mut self,
alloc: &A,
capacity: usize,
hasher: &dyn Fn(&mut Self, usize) -> u64,
fallibility: Fallibility,
layout: TableLayout,
) -> Result<(), TryReserveError>
where
A: Allocator,
{
// SAFETY: We know for sure that `alloc` and `layout` matches the [`Allocator`] and [`TableLayout`]
// that were used to allocate this table.
let mut new_table = self.prepare_resize(alloc, layout, capacity, fallibility)?;
// SAFETY: We know for sure that RawTableInner will outlive the
// returned `FullBucketsIndices` iterator, and the caller of this
// function ensures that the control bytes are properly initialized.
for full_byte_index in self.full_buckets_indices() {
// This may panic.
let hash = hasher(self, full_byte_index);
// SAFETY:
// We can use a simpler version of insert() here since:
// 1. There are no DELETED entries.
// 2. We know there is enough space in the table.
// 3. All elements are unique.
// 4. The caller of this function guarantees that `capacity > 0`
// so `new_table` must already have some allocated memory.
// 5. We set `growth_left` and `items` fields of the new table
// after the loop.
// 6. We insert into the table, at the returned index, the data
// matching the given hash immediately after calling this function.
let (new_index, _) = new_table.prepare_insert_slot(hash);
// SAFETY:
//
// * `src` is valid for reads of `layout.size` bytes, since the
// table is alive and the `full_byte_index` is guaranteed to be
// within bounds (see `FullBucketsIndices::next_impl`);
//
// * `dst` is valid for writes of `layout.size` bytes, since the
// caller ensures that `table_layout` matches the [`TableLayout`]
// that was used to allocate old table and we have the `new_index`
// returned by `prepare_insert_slot`.
//
// * Both `src` and `dst` are properly aligned.
//
// * Both `src` and `dst` point to different region of memory.
ptr::copy_nonoverlapping(
self.bucket_ptr(full_byte_index, layout.size),
new_table.bucket_ptr(new_index, layout.size),
layout.size,
);
}
// The hash function didn't panic, so we can safely set the
// `growth_left` and `items` fields of the new table.
new_table.growth_left -= self.items;
new_table.items = self.items;
// We successfully copied all elements without panicking. Now replace
// self with the new table. The old table will have its memory freed but
// the items will not be dropped (since they have been moved into the
// new table).
// SAFETY: The caller ensures that `table_layout` matches the [`TableLayout`]
// that was used to allocate this table.
mem::swap(self, &mut new_table);
Ok(())
}
写到这里,笔者已经被这个问题纠缠了两周,不堪忍受的我决定开始人肉找规律,将所有的Hash值转换为二进制,看看归于同一组的Hash到底有什么相同之处。
Inserted 1, hash = 33bd1e335a4e43f0, h2 = 19, map capacity = 3
Inserted 3, hash = 56303fd171416940, h2 = 2b, map capacity = 3
Inserted 15, hash = cde8088c422f9d0, h2 = 6, map capacity = 3
Inserted 22, hash = 411807d47ecb5b61, h2 = 20, map capacity = 7
Inserted 23, hash = bbf28bf43ce33881, h2 = 5d, map capacity = 7
Inserted 45, hash = 217bed8f242fc391, h2 = 10, map capacity = 7
Inserted 46, hash = d97613d73c3edd81, h2 = 6c, map capacity = 7
Inserted 48, hash = ec9ec7fbb5226711, h2 = 76, map capacity = e
Inserted 53, hash = ea21590131a0aad0, h2 = 75, map capacity = e
Inserted 55, hash = 6e28ebd650236d51, h2 = 37, map capacity = e
Inserted 59, hash = 263478baaf15b7f1, h2 = 13, map capacity = e
Inserted 60, hash = 2aebb2b8fdb4f070, h2 = 15, map capacity = e
Inserted 73, hash = 163193d2c2c5b7c1, h2 = b, map capacity = e
Inserted 78, hash = a8f5a0a55cea2e21, h2 = 54, map capacity = e
Inserted 85, hash = dbe1512d01714890, h2 = 6d, map capacity = 1c
Inserted 87, hash = 1159a3327874fea1, h2 = 8, map capacity = 1c
22:0110│ 0x5555555bdf40 ?— 0x1513377576100619
23:0118│ 0x5555555bdf48 ?— 0xffffffffffffff6d
24:0120│ 0x5555555bdf50 ?— 0xff08540b6c5d202b
25:0128│ 0x5555555bdf58 ?— 0xffffffffffffffff
0011 0011 1011 1101 0001 1110 0011 0011 0101 1010 0100 1110 0100 0011 1111 0000
0000 1100 1101 1110 1000 0000 1000 1000 1100 0100 0010 0010 1111 1001 1101 0000
0010 0001 0111 1011 1110 1101 1000 1111 0010 0100 0010 1111 1100 0011 1001 0001
1110 1100 1001 1110 1100 0111 1111 1011 1011 0101 0010 0010 0110 0111 0001 0001
1110 1010 0010 0001 0101 1001 0000 0001 0011 0001 1010 0000 1010 1010 1101 0000
0110 1110 0010 1000 1110 1011 1101 0110 0101 0000 0010 0011 0110 1101 0101 0001
0010 0110 0011 0100 0111 1000 1011 1010 1010 1111 0001 0101 1011 0111 1111 0001
0010 1010 1110 1011 1011 0010 1011 1000 1111 1101 1011 0100 1111 0000 0111 0000
1101 1011 1110 0001 0101 0001 0010 1101 0000 0001 0111 0001 0100 1000 1001 0000
0101 0110 0011 0000 0011 1111 1101 0001 0111 0001 0100 0001 0110 1001 0100 0000
0100 0001 0001 1000 0000 0111 1101 0100 0111 1110 1100 1011 0101 1011 0110 0001
1011 1011 1111 0010 1000 1011 1111 0100 0011 1100 1110 0011 0011 1000 1000 0001
1101 1001 0111 0110 0001 0011 1101 0111 0011 1100 0011 1110 1101 1101 1000 0001
0001 0110 0011 0001 1001 0011 1101 0010 1100 0010 1100 0101 1011 0111 1100 0001
1010 1000 1111 0101 1010 0000 1010 0101 0101 1100 1110 1010 0010 1110 0010 0001
0001 0001 0101 1001 1010 0011 0011 0010 0111 1000 0111 0100 1111 1110 1010 0001
上面最后的几大行二进制数据中,上面的是保存到第一组的Hash,下面的是保存到第二组的Hash,看出来有什么规律了吗?可以发现,上面的Hash中所有的第5低的bit均为1,下面的均为0。为了严谨考虑,笔者增加了数据量进行了进一步测试,发现当组数为4时,是按照第5低bit和第6低bit来判断一个数据应该被分到哪组。
至此,我们最终通过实验获知了Rust中的HashMap的分组方式,与传统的SwissTable不同,分组的标志位从第5低bit开始,这也是为什么笔者一开始找了很长时间源码与规律依然一无所获。
下面是笔者的测试程序,读者可以将这个程序编译后通过gdb调试进行HashMap内存空间的一一比对。
use std::collections::HashMap;
use std::hash::{BuildHasher, Hash, Hasher};
pub fn main() {
let rs = std::collections::hash_map::RandomState::new();
let mut map: HashMap<u64, u64> = HashMap::with_hasher(rs);
let mut ctr = [0;4];
for i in 0..1000u64 {
let mut hasher = map.hasher().build_hasher();
i.hash(&mut hasher);
let hash = hasher.finish();
if ctr[(hash as usize >> 4) & 3] == 13 { continue }
if ctr[0] + ctr[1] + ctr[2] + ctr[3] == 13 * 4 { break }
let h2 = hash >> 57;
map.insert(i, i);
println!("Inserted {i:<02}, hash = {hash:<064b}, h1(suspected) = {:x}, h2 = {:x}, map capacity = {:x}",
(hash >> 4) & 3, h2, map.capacity());
ctr[(hash as usize >> 4) & 3] += 1;
}
println!("Finished!");
}
在实际测试过程中,当数据量较大时,经常需要线性后移,即当前组已满,需要将Hash值移动到后面一个组中。实际调试时发现,一个组中似乎最多只会保存15个数据而不是填充满,在几次调试后均未发现填充满的组。
另外需要注意的是,在保存HashMap的堆Chunk中,数据的排布方式有一些独特。数据保存在SwissTable之前,设SwissTable的起始地址为x,那么x+i处标志字节所对应的数据地址位于x-sizeof(key+value)*i,笔者猜测这样是为了便于Rust进行寻址,因为对HashMap的操作中,普遍是传入的SwissTable地址而非数据的起始地址,这样可以在不知道数据起始地址的情况下快速对应到数据。而对于SwissTable,若实际的组数为2n,那么保存到堆中的组应该为2n+1,最后一组与第一组的数据相同。这可能是为了在最后一组满且需要保存数据时能够快速检测到需要遍历到第一组添加数据。
总结
本文的信息量比较大,下面我们来简单总结一下。
- 对于Rust,其HashMap的底层实现是SwissTable,这是一种高效的HashMap算法。
- Rust在HashMap中使用的默认Hash算法是SipHash算法。
- Rust会保证所有组至少留出1/8的空闲空间,如果下一次添加数据打破了这一规则,Rust将对组进行扩充。
- Rust将Hash去掉最低4位和最高7位,剩余的值作为组的索引值,其值对组数取模后的值即为一个键值对应该被保存的组号。如果组满则实行线性规则在后面的组中插入。
- Rust在初始化HashMap时使用两个随机数作为Hash算法的参数,这使得相同的键值对在不同的HashMap中计算的Hash值也不同。
- Rust的HashMap其余规则与SwissTable定义的规则没有什么太大的区别。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!