蚁群优化算法ACO
2023-12-14 19:04:48
蚁群优化算法模拟了自然界中蚂蚁的觅食行为,信息素浓度的大小表征路径的远近,信息素浓度越高,表示对应的路径距离越短。同时,路径上的信息素浓度会随着时间的推进而逐渐衰减。
1.过程
(1)初始化参数
蚁群规模、信息素因子α、启发函数因子β、信息素挥发因子ρ、信息素释放总量q、最大迭代次数等。
(2)构建解空间
起初把蚂蚁随机放到不同城市,对于每一个蚂蚁,采用轮盘赌找出下一个要访问的城市,直到访问完所有城市。
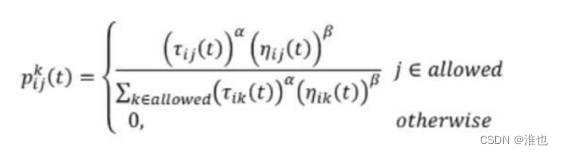
(3)更新信息素
计算各个蚂蚁经过的路径长度,找出本次迭代中的最短路径,并更新城市路径的信息素浓度。更新信息素浓度分为三种策略:蚁周、蚁量、蚁密。
蚁周是完成一次路径循环后,蚂蚁才释放信息素。
蚁量是一只蚂蚁从一个城市到达另一个城市后,直接释放信息素。
蚁密是一只蚂蚁从一个城市到达另一个城市后,释放的信息素需要除以城市间的路径距离。
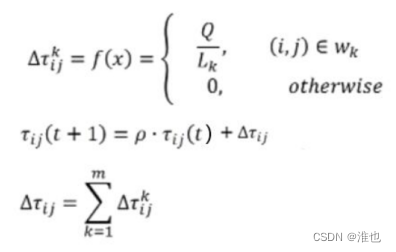
(4)判断是否终止
迭代次数到达最大迭代次数后,终止。否则,回到(2)。
2.流程图

3.代码
from utils import draw_picture, get_next_pos, init_pos, save_best_result
import tqdm
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('TkAgg')
class ACO(object):
def __init__(self, ant_count: int, generations: int, alpha: float, beta: float, rho: float, q: int,
strategy: int, distance, points):
"""
:param ant_count:
:param generations:
:param alpha: relative importance of pheromone
:param beta: relative importance of heuristic information
:param rho: pheromone residual coefficient
:param q: pheromone intensity
:param strategy: pheromone update strategy. 0 - ant-cycle, 1 - ant-quality, 2 - ant-density
:param distance: distance between each points
"""
self.Q = q
self.rho = rho
self.beta = beta
self.alpha = alpha
self.ant_count = ant_count
self.generations = generations
self.update_strategy = strategy
self.points = points
self.distance = distance
# 路径数目
self.rank = len(distance)
#
self.eta = [[0 if i == j else 1 / distance[i][j] for j in range(self.rank)] for i in
range(self.rank)]
# 每条路径上的信息素浓度
self.pheromone_content = [[1 for _ in range(self.rank)] for _ in range(self.rank)]
# 初始化
def initialization(self):
self.memory_vector = [] # 记录每个蚂蚁的总路径
for _ in range(self.ant_count): # 不关心i,可以用_代替i
self.memory_vector.append([init_pos(self.rank)]) # 随机初始化每个蚂蚁位置
# 用轮盘赌计算蚂蚁要去的下一个城市
def roulette(self, id, pos):
possibility = []
for i in range(self.rank):
if i in self.memory_vector[id]:
# 如果蚂蚁访问过这个城市,则不去
possibility.append(0)
else:
possibility.append(self.pheromone_content[pos][i]**self.alpha*(self.eta[pos][i]**self.beta))
next_pos = get_next_pos(possibility)
return next_pos
# 增加信息素浓度:三种策略,这里还有点问题
def update_pheromone_delta(self, ant_path):
if self.update_strategy == 0:
for i in range(self.ant_count):
self.pheromone_content[ant_path[i][0]][ant_path[i][1]] += self.Q
self.pheromone_content[ant_path[i][1]][ant_path[i][0]] += self.Q
if len(self.memory_vector[0]) == self.rank:
self.pheromone_content[self.memory_vector[i][-1]][self.memory_vector[i][0]] += self.Q
self.pheromone_content[self.memory_vector[i][0]][self.memory_vector[i][-1]] += self.Q
elif self.update_strategy == 1:
for i in range(self.ant_count):
self.pheromone_content[ant_path[i][0]][ant_path[i][1]] += (self.Q/self.distance[ant_path[i][0]][ant_path[i][1]])
self.pheromone_content[ant_path[i][1]][ant_path[i][0]] += (self.Q/self.distance[ant_path[i][0]][ant_path[i][1]])
if len(self.memory_vector[0]) == self.rank:
self.pheromone_content[self.memory_vector[i][-1]][self.memory_vector[i][0]]+=self.Q/self.distance[self.memory_vector[i][0]][self.memory_vector[i][-1]]
self.pheromone_content[self.memory_vector[i][0]][self.memory_vector[i][-1]]+=self.Q/self.distance[self.memory_vector[i][0]][self.memory_vector[i][-1]]
elif self.update_strategy == 2:
# 完成一次循环后
if len(self.memory_vector[0]) == self.rank:
# 计算每个蚂蚁本次的总路程
total_cost = []
for i in range(self.ant_count):
cost = 0
for j in range(1, self.rank):
cost += self.distance[self.memory_vector[i][j-1]][self.memory_vector[i][j]]
cost += self.distance[self.memory_vector[i][0]][self.memory_vector[i][-1]]
total_cost.append(cost)
# 更新信息素浓度
for i in range(self.ant_count):
delta = self.Q/total_cost[i]
for j in range(1, self.rank):
# 双向路径
self.pheromone_content[self.memory_vector[i][j-1]][self.memory_vector[i][j]] += delta
self.pheromone_content[self.memory_vector[i][j]][self.memory_vector[i][j-1]] += delta
# 蚂蚁最初的那条路
self.pheromone_content[self.memory_vector[i][0]][self.memory_vector[i][-1]] += delta
self.pheromone_content[self.memory_vector[i][-1]][self.memory_vector[i][0]] += delta
else:
# 没有完成一次循环
pass
else:
raise KeyError
# 减少信息素浓度
def update_pheromone(self):
for i in range(self.rank):
for j in range(self.rank):
self.pheromone_content[i][j] = self.pheromone_content[i][j] * (1 - self.rho)
# 更新蚂蚁本次迭代找到的路径
def update_memory_vector(self, ant_path):
for i in range(self.ant_count):
self.memory_vector[i].append(ant_path[i][1])
# 执行算法
def run(self):
self.cost = 0
self.path = []
plt.ion() # 启用交互模式(动态图)
# tqdm进度条
for iteration in tqdm.tqdm(range(self.generations), desc='Processing'):
# print(f'-----start iteration {iteration+1} of ACO-----')
self.initialization()
for steps in range(self.rank - 1):
# 在一次新的迭代中,蚂蚁选择一条路径从pos到next_pos
ant_path = []
for i in range(self.ant_count): # 对于每一只蚂蚁
pos = self.memory_vector[i][-1]
next_pos = self.roulette(i, pos)
ant_path.append([pos, next_pos])
self.update_memory_vector(ant_path) # 更新蚂蚁本次迭代的路径
self.update_pheromone_delta(ant_path) # 增加路径上的信息素浓度
self.update_pheromone() # 减少信息素浓度
plt.cla()
plt.title("ant colony algorithm")
self.cost, self.path = draw_picture(self.points, self.distance, self.memory_vector, iteration)
plt.pause(0.01) # 暂停运行一段时间,能将内存中的图像显示出来
# 保存数据
def save(self, seed):
save_best_result(self.path, self.points, seed)
plt.ioff() # 关闭交互模式
plt.show() # 显示图片,会阻塞后面代码运行,适用于静态图
# 开发时间:2023/12/13 19:50
import random
import math
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('TkAgg')
def random_init(points_num ,min_x ,max_x, min_y, max_y):
points = []
while len(points) != points_num:
x = random.randint(min_x, max_x)
y = random.randint(min_y, max_y)
if [x, y] in points:
continue
points.append([x, y])
file = open("temp.txt", "w")
for i in range(len(points)):
file.write(f'{points[i][0]}{points[i][1]}\n')
file.close()
print("Data running time was saved in file [temp.txt]")
return points
def dis(point1, point2):
return math.sqrt((point1[0]-point2[0]) ** 2 + (point1[1]-point2[1]) ** 2)
def calculate_distance(points):
distance = []
for i in range(len(points)):
list = []
for j in range(len(points)):
list.append(dis(points[i], points[j]))
distance.append(list)
return distance
def get_next_pos(possibility):
n = sum(possibility)
for i in range(len(possibility)):
possibility[i] /= n
n = sum(possibility)
r = random.uniform(0, n)
pos = 0
while True:
if possibility[pos] == 0:
pos += 1
elif r-possibility[pos] < 0:
return pos
else:
r -= possibility[pos]
pos += 1
def init_pos(rank):
pos = random.randint(0, rank-1)
return pos
def load_example(text_name):
file = open(text_name, 'r')
content = file.readlines()
points = []
for data in content:
x, y = data.split(" ")
points.append([int(x), int(y)])
distance = calculate_distance(points)
return points, distance
def draw_picture(points, distance, path, iteration):
rank = len(points)
ant_number = len(path)
x = []
y = []
for i in range(rank):
x.append(points[i][0])
y.append(points[i][1])
plt.scatter(x, y)
min_cost = np.inf
for i in range(ant_number):
temp_cost = 0
for j in range(1, rank):
temp_cost += distance[path[i][j-1]][path[i][j]]
temp_cost += distance[path[i][0]][path[i][-1]]
if temp_cost < min_cost:
min_cost = temp_cost
best_path = path[i]
for i in range(ant_number):
for j in range(rank):
x[j] = points[path[i][j]][0]
y[j] = points[path[i][j]][1]
plt.plot(x, y)
plt.text(0, 0, f'iteration:{iteration} min_cost = {round(min_cost, 2)}', family='fantasy', fontsize=12,style='italic',color='mediumvioletred')
return round(min_cost, 2), best_path
def save_best_result(path, points, seed):
for i in range(1, len(path)):
x1 = points[path[i - 1]][0]
y1 = points[path[i - 1]][1]
x2 = points[path[i]][0]
y2 = points[path[i]][1]
plt.arrow(x1, y1, x2 - x1, y2 - y1, width=0.05, color='r', length_includes_head=True)
plt.arrow(x2, y2, points[path[0]][0] - x2, points[path[0]][1] - y2, width=0.05, color='r',
length_includes_head=True)
plt.gcf().set_size_inches(20, 12) # get current figure
plt.savefig("result.png")
print("画图呀")
plt.close()
print('\n')
print("-" * 50)
print(f"[Best Path](random seed [{seed}])")
print(show_path(path))
print("Last result picture was saved in [result.png]")
print(f"If you want to get this result again please add '-s {seed}'")
print("-" * 50)
print('\n')
def show_path(path):
route = str(path[0])
for i in range(1, len(path)):
route = route + "->"+str(path[i])
route = route + "->"+str(path[0])
return route
import argparse
from ACO import ACO
import random
from utils import random_init,calculate_distance,load_example
import matplotlib
matplotlib.use('TkAgg')
def default_argument_parser():
# ArgumentParser 编写命令行接口
# 创建对象(解析器)
parser = argparse.ArgumentParser(description="ant colony algorithm")
# 添加参数
parser.add_argument("--test", nargs="?") # 参数可设置0或1个
parser.add_argument('--ant', default=5, type=int) # 蚂蚁数
parser.add_argument('--points', default=20, type=int) # 城市数
parser.add_argument('--generation', default=50,type=int) # 迭代次数
parser.add_argument('--alpha', default=2.0,type=float) # 信息素因子
parser.add_argument('--beta', default=3.0,type=float) # 启发函数因子
parser.add_argument('--rho', default=0.5,type=float) # 信息素挥发因子
parser.add_argument('--q', default=100,type=float) # 信息素浓度
parser.add_argument('--strategy', default=2,type=int) # 信息素更新策略
parser.add_argument('--min_x', default=0,type=int) # 范围
parser.add_argument('--max_x', default=100,type=int)
parser.add_argument('--min_y', default=0,type=int)
parser.add_argument('--max_y', default=100,type=int)
parser.add_argument('-s', '--seed', type=int)
'''
信息素三种更新策略
0: 蚁量:加浓度
1: 蚁密:加浓度/城市间的路径距离
2: 蚁周:蚂蚁全走完再更新信息素浓度
'''
return parser
def main():
# 解析参数
args = default_argument_parser().parse_args()
if(args.seed == None):
seed = random.randint(1, 10000)
random.seed(seed) # 随机数种子
print("no random seed found")
args.seed = seed
else:
print(f"set random seed {args.seed}")
random.seed(args.seed)
if args.test != None:
points, distance = load_example(args.test)
else:
points = random_init(args.points, args.min_x, args.max_x, args.min_y, args.max_y)
distance = calculate_distance(points)
aco = ACO(
ant_count=args.ant,
generations=args.generation,
alpha=args.alpha,
beta=args.beta,
rho=args.rho,
q=args.q,
strategy=args.strategy,
points=points,
distance=distance,
)
aco.run() # 执行算法
aco.save(args.seed) # 保存数据
# 当.py文件被直接运行时,下面代码会执行;当.py文件以模块形式被导入则不会执行
if __name__ == '__main__':
main()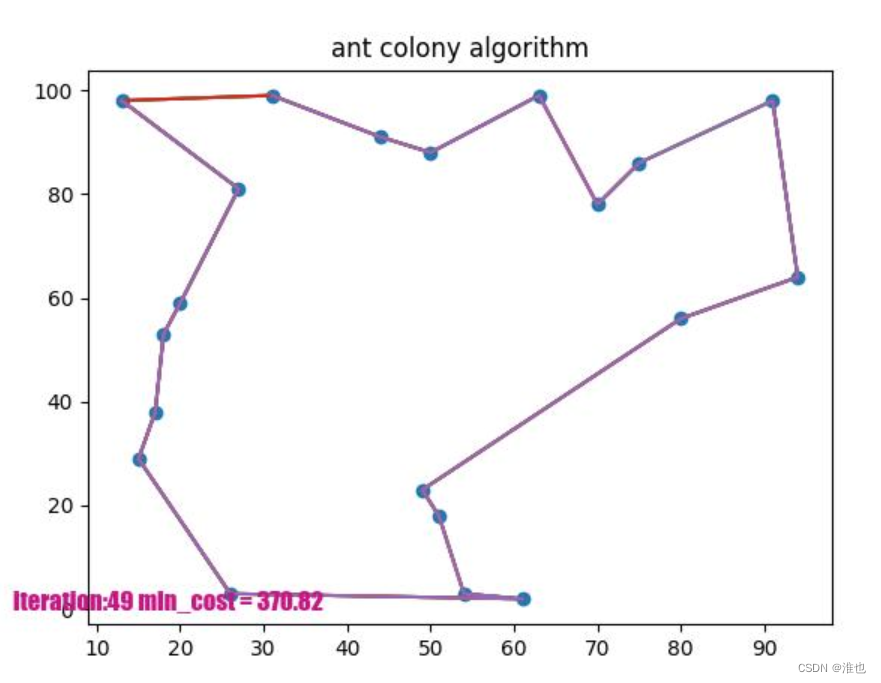
4.优缺点
优点:采用正反馈机制进行更新,使得结果不断收敛;可以并行计算。
缺点:收敛速度慢;不适用于解空间是连续的优化问题。
文章来源:https://blog.csdn.net/qq_51165184/article/details/134980423
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!