[嵌入式专栏](FOC - SVPWM马鞍波)

---

【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485

---

1 . 前言

SVPWM为什么是马鞍波形状，为什么不是正弦波，以下深入浅出探讨这个概念

2 . 内容

根据之前扇区判断，进行扇区计算得出TxTy后，根据TxTy计算可以得到TaTbTc，注意这里的TaTbTc并不是最终驱动硬件开关管的信号，而是对每个扇区的TxTy进行三次谐波的区分，后面具体驱动硬件开关管，要根据对应扇区分配谐波分量

从上到下来看，数值大小不必在意，只是为了把信号区分开，从而做了偏置

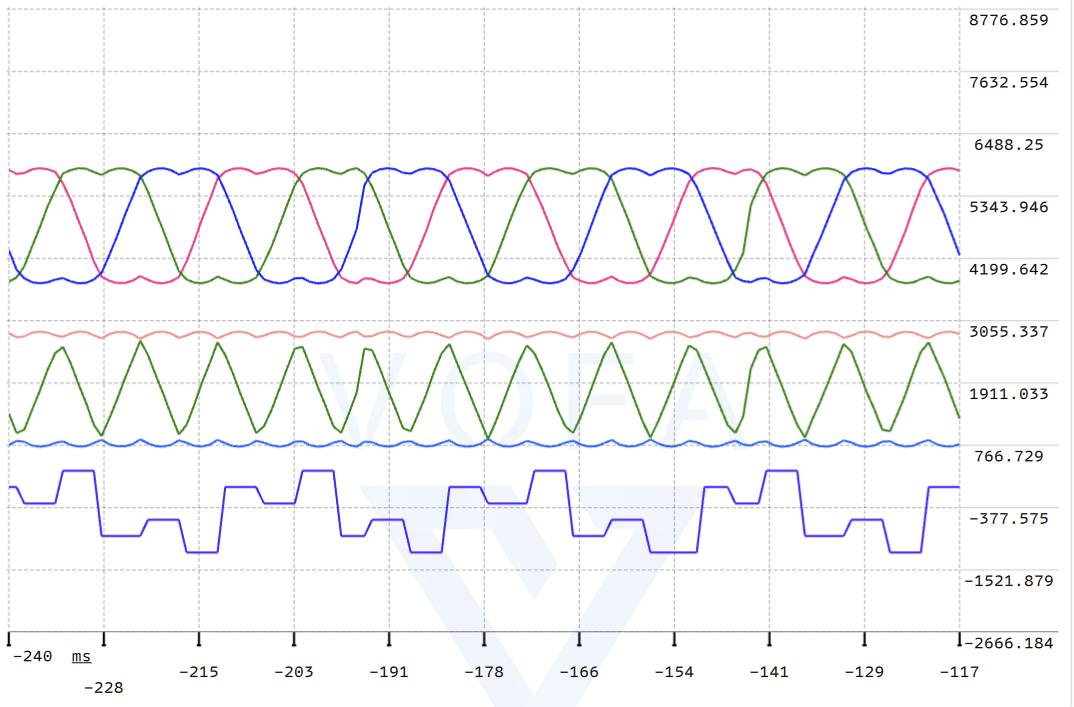
4199-6488区间为最终输出给芯片pwm比较器进行比较输出的信号

• 粉色波形 ：$T_{outA}$
• 绿色波形 ：$T_{outB}$
• 蓝色波形 ：$T_{outC}$

766-3055区间为三次谐波

• 蓝色波形 ：Ta
• 绿色波形 ：Tb
• 粉色波形 ：Tc

-1521-766区间为$N_{扇区关系值}$

• 蓝色波形 ：$N$

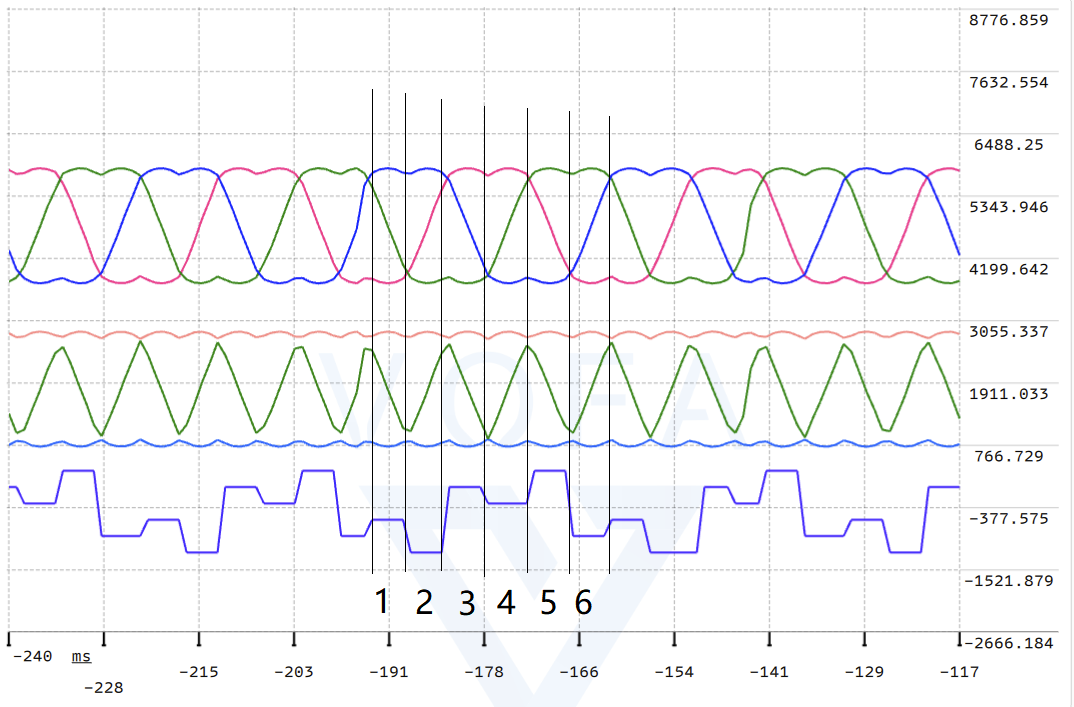这里画出实际扇区对应区间，可以直观看到三次谐波合成最终输出信号的效果，每个扇区对应的三次谐波位置，以及最终输出给硬件开关管经过RC低通滤波后的信号波形。

【Q】为什么三次谐波TaTbTc是这个样子？
【A】回顾扇区计算可以看到$U_{dc}$取的$\frac{2}{3}$，结合矢量合成的角度运算后得出的TxTy，以下给出TaTbTc与每个扇区TxTy的关联

• Ta = Ts - (Tx + Ty) / 4
• Tb = Ta + Tx / 2
• Tc = Tb + Ty / 2

当拿到TaTbTc后，可以根据扇区315462的关系转换分配$Ta，Tb，Tc$到$T_{outA}$，$T_{outB}$，$T_{outC}$

每个扇区进行七段式驱动PWM循环，也可以五段式，为什么要这样切换来做PWM，因为每次变化只需要变化一次开关管状态，这样电流谐波少，并且开关损耗低，当然五段式的损耗会更低，但是电流谐波会大一点。

扇区	七段式切换
扇区一	000-100-110-111-111-110-100
扇区二	000-010-110-111-111-110-010
扇区三	000-010-011-111-111-011-010
扇区四	000-001-011-111-111-011-001
扇区五	000-001-101-111-111-101-001
扇区六	000-100-101-111-111-101-100

【Q】把UαUβ的值代入就可以计算出TxTy，把TxTy代入就可以计算出TaTbTc，把值以时间轴呈现就是上面的波形，但波形为什么是这样？最起始的根本原因是什么？
【A】想象一下Uα与Uβ相位相差90°，又因为矢量合成里与下方ABC中的关系，基于下方的关系可以计算出当θ在30°，150°，210°，330度时，Ta与Tc呈现出极限值，因此波形上看起来才会是有凸出的效果

【Q】那么下方的关系值又是怎么得到的？
【A】回顾扇区判断与扇区计算可以直观了解到每个扇区基于运算化简最终得出下方的关系

A	B	C
$U\beta$	$?\frac{\sqrt{3}}{2}U\alpha ?\frac{1}{2}U\beta$	$\frac{\sqrt{3}}{2}U\alpha ?\frac{1}{2}U\beta$

3 . 小结

现在看，为什么SVPWM是马鞍波这个疑问，根据以上讲述细节的由来可得到答案，正因为有了谐波的最大最小值，由三次谐波合成后的结果随时间轴呈现出的效果为马鞍波形状。

技术交流QQ群 : 745662457
群内专注 - 问题答疑，项目外包，技术研究