经典文献阅读之--Online Monocular Lane Mapping(使用Catmull-Rom样条曲线完成在线单目车道建图)
0. 简介
对于单目摄像头完成SLAM建图这类操作,对于自动驾驶行业非常重要,《Online Monocular Lane Mapping Using Catmull-Rom Spline》介绍了一种仅依靠单个摄像头和里程计生成基于样条的在线单目车道建图方法。我们提出的技术将车道关联过程建模为一个二分图的分配问题,并通过结合Chamfer距离、姿态不确定性和横向序列一致性为边赋予权重。此外,文中还精心设计了控制点初始化、样条参数化和优化,以逐步创建、扩展和精化样条。相关的代码已经在Github上开源了。
1. 主要贡献
基于Catmull-Rom样条表示,设计了一个完整的在线车道建图系统,如图1所示。所提出的系统允许自动驾驶车辆使用时间图像和里程计数据实时构建局部车道地图,这可以用于自我定位、规划和众包更新[4]。总体而言,具体贡献可以总结如下:
- 我们提出了一个在线单目车道映射系统,包括车道跟踪和地图优化子系统。该系统可以直接输出由Catmull-Rom样条表示的轻量级实例级车道地图,无需离线矢量化。
- 系统的每个部分都经过精心设计,结合了车道标线和样条的特性,包括车道关联、姿态估计、样条初始化、扩展和优化。
- 在公开可用的数据集OpenLane上的实验表明,我们提出的方法可以改善车道关联、里程计精度和地图质量。
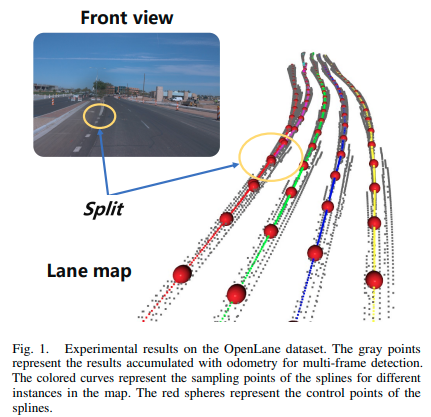
图1. 在OpenLane数据集上的实验结果。灰色点表示使用里程计进行多帧检测的累积结果。彩色曲线表示地图中不同实例的样本点的样条曲线。红色球体表示样条曲线的控制点。
2. 系统概述
所提出的单目车道映射系统的结构如图2所示。该系统使用仅有的单目摄像头和里程计(例如VIO、LIO)作为输入,无需先验导航地图或航空照片,即可输出紧凑的车道标记地图,以样条表示。具体而言,所提出的框架由两个子系统组成:车道跟踪和地图优化。神经网络在车道跟踪中直接基于输入图像预测3D车道标记。然后,这些预测结果经过进一步处理以满足后续需求,详见第3.1节。随后,处理后的车道标记与地图中的车道标记结合,同时考虑里程计提供的位姿信息(第3.2节)。最后,根据关联结果更新位姿(参见第3.3节)。在地图优化中,样条首先从零开始初始化,或者根据新获得的检测结果进行扩展(第4.1节)。最后,应用增量优化框架iSAM2 [28],通过添加新的观测来逐步更新地图中的样条,而不会丢失过去观测的信息(第4.2节)。
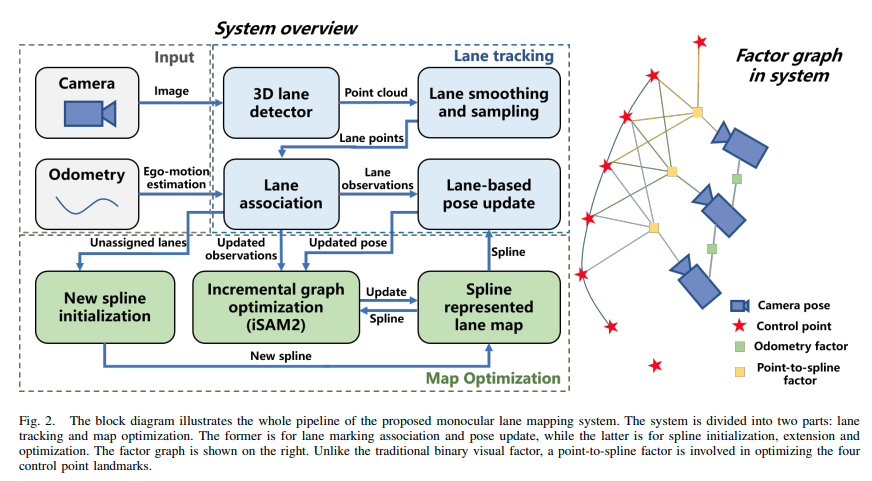
图2. 该块图示了提出的单目车道映射系统的整个流程。该系统分为两个部分:车道跟踪和地图优化。前者用于车道标记关联和姿态更新,而后者用于样条曲线的初始化、扩展和优化。右侧显示了因子图。与传统的二进制视觉因子不同,优化过程中涉及到了点到样条曲线的因子,用于优化四个控制点地标。
3. 车道跟踪
3.1 车道表示
在这项研究中,我们使用Persformer [12]来获得车道检测结果,其中包括无序的车道标记点及其相关的实例级标签。此外,我们区分车道的表示方式,包括观测(检测)和地标(地图)。特别地,对于网络预测结果,考虑到其稀疏性和噪声,我们首先将其转换为本地参考框架(LRF),其中车道的主要方向与X轴对齐。随后,我们对X-Y和X-Z坐标进行三次多项式拟合,并以特定分辨率进行采样(在我们的实验中设定为0.5米)。因此,车道观测结果可以表示为:
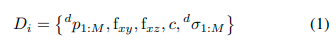
在检测到的车道上, d p 1 : M ∈ R 3 ^dp_{1:M} ∈ \mathbb{R}^3 dp1:M?∈R3 是采样点, f x y f_{xy} fxy? 和 f x z f_{xz} fxz? 分别是多项式系数, c c c 是类别(例如,双黄线,白实线)。 d σ 1 : M ^dσ_{1:M} dσ1:M? 是检测噪声的标准差,可以设置为与点的2-范数成比例。
地图中的车道地标由 Catmull-Rom 样条表示,写作 L j = { P 0 : N + 1 , c } L_j = \{P_{0:N+1}, c\} Lj?={P0:N+1?,c},其中 P 0 : N + 1 P_{0:N+1} P0:N+1? 是样条中的控制点, c c c 是类别。分段样条曲线 L j L_j Lj? 有 N N N 个段(每两个段共享三个控制点),每个段 l l l 有四个相邻的控制点来确定曲线的点 l p ( u ) ^lp(u) lp(u)。
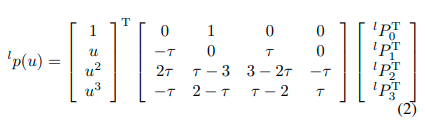
其中 u ∈ [ 0 , 1 ] u ∈ [0, 1] u∈[0,1]被称为参数。找到与曲线上的点对应的 u u u的过程被称为参数化; τ τ τ控制曲线的混合程度,通常设置为1/2。不失一般性,我们将这四个控制点称为 [ l P 0 , l P 1 , l P 2 , l P 3 ] [^lP_0,^lP_1,^lP_2,^lP_3] [lP0?,lP1?,lP2?,lP3?]。在后面的部分,为了简洁起见, l l l和 d d d可能会被省略。在这种情况下,曲线上的一个点可以被视为四个控制点的加权。这些系数在图3(a)中显示。
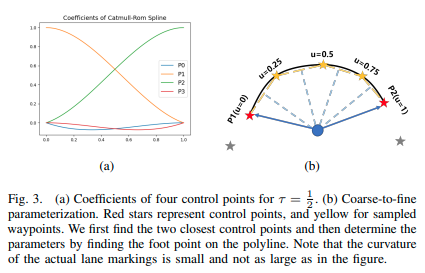
图3. (a) τ = 1 / 2 τ = 1/2 τ=1/2 时的四个控制点系数。(b) 粗到细的参数化。红色星星代表控制点,黄色代表采样的路径点。我们首先找到最近的两个控制点,然后通过在折线上找到垂足确定参数。请注意,实际车道标线的曲率较小,不像图中那么大。
3.2 车道关联(重点内容)
给定一组检测 D D D和一组地标 L L L,车道关联旨在将检测 D i D_i Di? 与现有的地标 L j L_j Lj? 匹配或识别出一个新的车道。为此,我们使用二分图将问题建模为一个分配问题,并使用 K ? M K-M K?M算法[29],[30]来解决,关键点在于如何确定边和它们的权重。首先,相关的车道应该具有相同的类别。另一个自然的想法是,可以先在样条线上采样一些点,然后计算两个点云之间的距离,例如Chamfer距离,来确定 D i D_i Di?与 L j L_j Lj?的相似性。然而,Chamfer距离总是可以计算的,因此二分图中的一个顶点将有一条边,导致不会生成新的车道标记。因此,受到最近的KISS-ICP[31]和Kim等人的工作[32]的启发,我们限制了搜索范围以及Chamfer距离的上界。
我们计算里程计和真实姿态之间的差异 ( ? R ,? t ) (?R,?t) (?R,?t)。与Lie群切空间中的噪声的传统假设不同,我们只使用两个参数,即旋转和平移的标准差,分别为 σ θ σ_θ σθ?和 σ t σ_t σt?,其中:
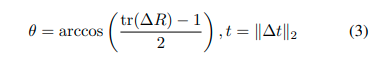
因此,对于 D i D_i Di?中的一个点 p k p_k pk?,其与真实匹配点之间的距离的上界 δ k δ_k δk?(使用95%的双标准差规则)可以表示为:
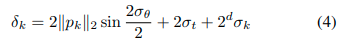
因此,鉴于样本点在样条曲线 q 1 : Q q_{1:Q} q1:Q?上,检测点 p 1 : M p_{1:M} p1:M?和里程计姿态 T T T,我们重新定义 D i D_i Di?和 L j L_j Lj?之间的距离为:
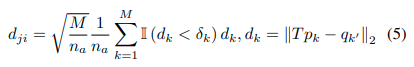
其中 n a n_a na?代表满足距离阈值的点的数量, I \mathbb{I} I是指示函数, q k ’ q_{k’} qk’?是 p k p_k pk?最近的采样点, M n a \sqrt{\frac{M}{n_a}} na?M??是乘以以惩罚低匹配率。此外,我们设置了一个上限 2 m e a n ( δ k ) \sqrt{2}mean(δ_k) 2?mean(δk?)来确定是否出现新的车道。 2 \sqrt{2} 2?表示至少有一半的点匹配。
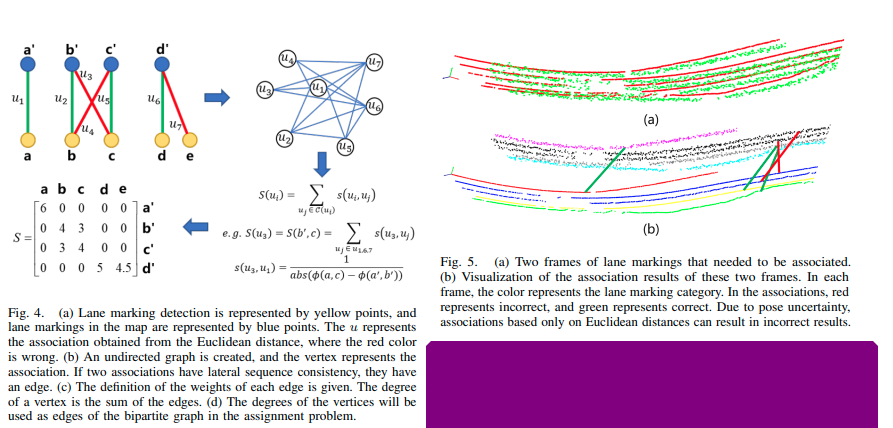
图4. (a) 车道标线检测由黄色点表示,地图中的车道标线由蓝色点表示。u表示通过欧几里德距离得到的关联,红色表示错误的关联。(b) 创建一个无向图,顶点表示关联。如果两个关联具有横向顺序一致性,则它们之间有一条边。? 给出了每条边的权重定义。顶点的度是边的总和。(d) 顶点的度将用作分配问题中二分图的边。
图5. (a) 需要关联的两个车道标线帧。 (b) 这两个帧的关联结果可视化。每个帧中,颜色代表车道标线的类别。在关联中,红色代表错误,绿色代表正确。由于姿态不确定性,仅基于欧氏距离的关联可能导致错误的结果。
尽管如此,仅仅依靠距离进行数据关联可能会导致歧义,特别是考虑到 ? R ?R ?R的存在,如图5所示。在欧几里得空间中,检测和地标之间并没有很好地分离,甚至交叉。为此,我们进一步使用横向顺序一致性对边进行加权。与大多数图匹配方法一样[33],我们定义了两个关联对(二分图中的边)之间的一致性。为了更好地说明数据关联,我们在图4中配置了一个示例。有四条车道,五个地标,基于欧几里得距离有七个关联对,其中三个是错误的(但仍在距离上限之内)。每个关联对在图中充当一个顶点。两个顶点之间是否存在边取决于它们产生的关联结果的横向顺序一致性。例如,在BEV中,对于 u 1 u_1 u1?和 u 3 u_3 u3?,我们在车道 b ’ b_’ b’?上采样两个点(例如起点和终点),创建一条直线,并确定车道 a ’ a_’ a’?的采样点(例如中间点)是否在直线上方或下方,再对于车道 c c c。如果它们具有相同的相对关系,则 u 1 u_1 u1?和 u 3 u_3 u3?之间存在一致性。此外, u 2 u_2 u2?和 u 3 u_3 u3?也不一致,因为它们共享地标 b ’ b_’ b’?。为了不失一般性,我们以 u 3 u_3 u3?为例计算其一致性得分 S ( u 3 ) S(u_3) S(u3?)。
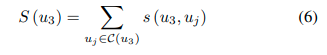
C C C表示与 u 3 u_3 u3?相连的顶点集。对于 u 3 u_3 u3?和 u 1 u_1 u1?,我们有
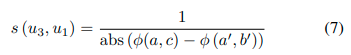
其中 a b s ( ? ) abs(·) abs(?)表示绝对值, ? ? ?表示先前提到的点到线距离的最小值。
最后,双分图的边可以通过两个分数相乘得到,其中一个是先前提到的Chamfer距离的倒数,另一个是 S S S中相应的横向序列一致性。
3.3 姿态更新
问题可以如下形式化。设 T t T_t Tt?表示相机在时间 t t t时相对于世界坐标系的姿态变换。结合第32节的关联结果,使用 T t T_t Tt?将 d p k ^dp_k dpk?投影到世界坐标系,通过找到关联样条上的足点 p ( u k ) p(u_k) p(uk?)来确定参数 u k u_k uk?。给定 p ( u k ) p(u_k) p(uk?)的局部方向 d k d_k dk?,定义了一个点到切线的残差,因为车道标线只提供了姿态估计的横向约束。注册的总体目标是找到
…详情请参照古月居
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!