动手学深度学习3 数据操作+数据预处理
1. 基础数据结构-N维数组
课件: https://courses.d2l.ai/zh-v2/assets/pdfs/part-0_4.pdf
视频:https://www.bilibili.com/video/BV1CV411Y7i4?p=1&vd_source=eb04c9a33e87ceba9c9a2e5f09752ef8
稍微有一点数学基础,更方便理解。
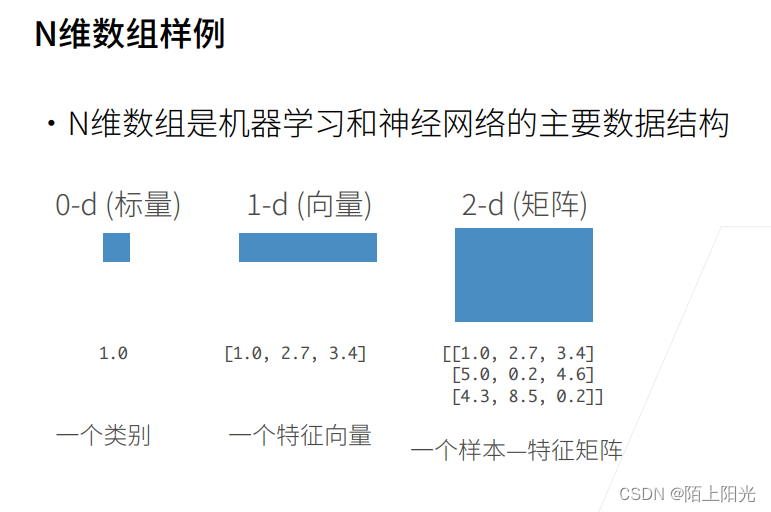
扩充到多维
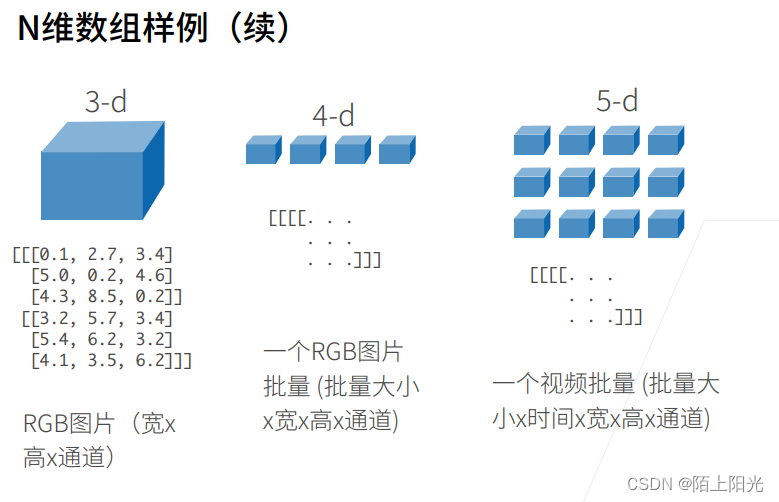
按逗号区分行列的处理操作
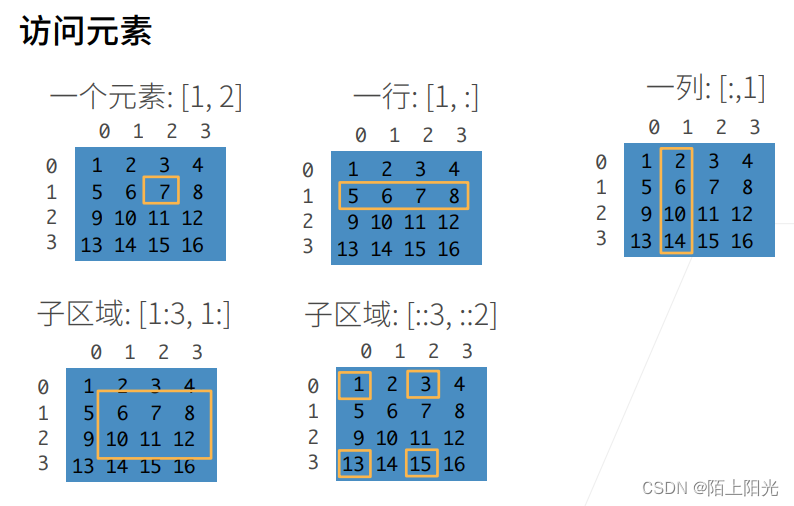
按冒号区分每行每列处理操作,单独一个冒号表示该行或该列所有的值,两个连续的冒号表示步长
索引从0开始
2. 数据操作实现–基础的张量运算
课件:https://zh-v2.d2l.ai/chapter_preliminaries/ndarray.html
视频:https://www.bilibili.com/video/BV1CV411Y7i4?p=2&vd_source=eb04c9a33e87ceba9c9a2e5f09752ef8
知乎运算详细文章:https://zhuanlan.zhihu.com/p/601792894
pytorch官方运算符文档:https://pytorch.org/docs/stable/torch.html
1. 张量–创建与赋值
1. 数据生成–创建 torch.arange
相当于python的range函数 range只生成整数,左闭右开区间,多用于循环中。
range() 函数可以接收 1 到 3 个参数,参数含义如下:
start: 序列的起始值,默认为 0
end: 序列的结束值(不包含该值)
step: 序列的步长,默认为 1
需要注意的是,range() 返回的是一个 range 对象,它只在需要时才将序列中的元素实际计算出来,因此在需要使用实际值时,需要将 range 对象转换成列表或迭代其中的元素。
torch.arange(start, end, step=1, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)是一个在给定范围内生成等间隔的值的函数。
参数:
start (float) – 序列起始值
end (float) – 序列结束值
step (float) – 序列步长
out (Tensor, optional) – 输出 Tensor
dtype (torch.dtype, optional) – 输出 Tensor 的数据类型
layout (torch.layout, optional) – 输出 Tensor 的布局
device (torch.device, optional) – 输出 Tensor 的设备
requires_grad (bool, optional) – 输出 Tensor 是否需要梯度
返回值:
torch.Tensor: 生成的等间隔序列
示例用法:
import torch
# 生成一个从 0 到 9 的等间隔序列
x = torch.arange(10)
print(x) # 输出: tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# 生成一个从 5 到 14 的等间隔序列,步长为 2
y = torch.arange(5, 15, 2)
print(y) # 输出: tensor([ 5, 7, 9, 11, 13])
创建张量
张量表示一个由数值组成的数组,这个数组可能有多个维度。 具有一个轴的张量对应数学上的向量(vector)【一维-1D】; 具有两个轴的张量对应数学上的矩阵(matrix)【二维-2D】; 具有两个轴以上的张量没有特殊的数学名称
** arange 创建一个行向量 ,默认创建为整数。也可指定创建类型为浮点数。张量中的每个值都称为张量的 元素(element)。例如,张量 x 中有 12 个元素。除非额外指定,新的张量将存储在内存中,并采用基于CPU的计算。**
x = torch.arange(12)
print(x)
# tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
2. 张量的属性–shape、numel
shape,来访问张量(沿每个轴的长度)的形状 。
print(x.shape)
#torch.Size([12])
.numel() , 获取张量中元素的总数大小(size) 永远是一个标量
print(x.numel()) # 调用的是一个函数
# 12
3. reshape–改变张量的shape但是不改变其值
相当于换了一个排列方式,更改数据的维度
reshape函数:改变一个张量的形状而不改变元素数量和元素值。 例如,可以把张量x从形状为(12,)的行向量转换为形状为(3,4)的矩阵。 这个新的张量包含与转换前相同的值,但是它被看成一个3行4列的矩阵。 要重点说明一下,虽然张量的形状发生了改变,但其元素值并没有变。 注意,通过改变张量的形状,张量的大小size不会改变。
x = x.reshape(3,4)
print(x)
print(x.shape)
print(x.numel())
#tensor([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]])
#torch.Size([3, 4])
#12
在PyTorch中,可以使用`torch.reshape()`函数来改变张量的形状。
具体用法如下:
import torch
# 创建一个 2x3 的张量
x = torch.tensor([[1, 2, 3], [4, 5, 6]])
# 将其 reshape 为 3x2 的张量
y = torch.reshape(x, (3, 2))
print(y)
# 输出:
# tensor([[1, 2],
# [3, 4],
# [5, 6]])
`torch.reshape(input, shape)`函数接受两个参数:
- input: 要改变形状的输入张量
- shape: 一个元组,表示新的形状
需要注意的是,使用`torch.reshape()`得到的结果与输入张量共享数据,即它们指向同一块内存,因此对结果张量的操作也会影响到原始张量。如果需要得到一个与输入张量完全独立的张量,可以使用`torch.reshape(input, shape).clone()`来得到一个新的张量。
另外,还可以使用`reshape`方法:
x = torch.tensor([[1, 2, 3], [4, 5, 6]])
y = x.reshape(3, 2)
print(y)
# 输出:
# tensor([[1, 2],
# [3, 4],
# [5, 6]])
在实际应用中,根据需要改变张量的形状是一个非常常见且有用的操作,可以帮助我们适应不同的任务和模型结构。
当一个维度被指定,另一个可以通过元素总数自动算出,例如: x.reshape(-1,4)或x.reshape(3,-1)来取代x.reshape(3,4)。
4. 初始化张量 ones zeros等
初始化一些全为0 或者全为1 或者从特定分布中随机采样的数值的 张量
print(torch.zeros(2, 3, 4))
# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],
#
# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])
print(torch.ones(2, 3, 4))
# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]],
#
# [[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])
# 从均值为0、标准差为1的标准高斯分布(正态分布)中随机采样。
print(torch.randn(2, 3, 4))
# tensor([[[ 0.5563, -0.0505, -0.4659, 0.0024],
# [ 1.8880, -0.7179, -0.0356, 1.0053],
# [ 1.4919, -0.5910, 0.8015, 1.4057]],
#
# [[-1.4535, -1.7574, -0.0341, -0.8562],
# [ 0.6910, -0.1713, 0.0521, 0.5390],
# [-0.1989, 2.1386, -0.8314, -0.6795]]])
通常会随机初始化参数的值,去构造数组来作为神经网络中的参数。
5. 使用python列表或嵌套列表为张量赋值
最外层的列表对应于轴0,第二的列表对应于轴1,以此类推
x = torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(x)
print(x.shape)
# tensor([[2, 1, 4, 3],
# [1, 2, 3, 4],
# [4, 3, 2, 1]])
# torch.Size([3, 4])
x = torch.tensor([[[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]])
print(x)
print(x.shape)
# tensor([[[2, 1, 4, 3],
# [1, 2, 3, 4],
# [4, 3, 2, 1]]])
# torch.Size([1, 3, 4])
2. 张量的运算
行列式的运算规则–按对应位置元素进行计算
1. 标准算术运算符(+、-、*、/和**) 加减乘除幂运算
x = torch.tensor([1.0, 2, 4, 8]) # 1.0 使该向量都为浮点数
y = torch.tensor([2, 2, 2, 2]) # 该向量都是整数
print(x, y)
print(x + y)
print(x - y)
print(x * y)
print(x / y)
print( x ** y) # **运算符是求幂运算
# tensor([1., 2., 4., 8.]) tensor([2, 2, 2, 2])
# tensor([ 3., 4., 6., 10.])
# tensor([-1., 0., 2., 6.])
# tensor([ 2., 4., 8., 16.])
# tensor([0.5000, 1.0000, 2.0000, 4.0000])
# tensor([ 1., 4., 16., 64.])
2. 指数运算 torch.exp()
x = torch.tensor([1.0, 2, 4, 8]) # 1.0 使该向量都为浮点数
print(torch.exp(x))
# tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
3. cat 张量拼接
向量点积和矩阵乘法
dim=0 按照第0维做向量拼接,按行拼接;
dim=1 按照第1维做向量拼接,按列拼接;
参数
.cat(以元组形式提供张量列表,给出沿哪个轴【哪个维度】连结)
X = torch.arange(12, dtype=torch.float32).reshape(3, 4)
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(torch.cat((X, Y), dim=0))
print(torch.cat((X, Y), dim=1))
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]])
# tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
# [ 4., 5., 6., 7., 1., 2., 3., 4.],
# [ 8., 9., 10., 11., 4., 3., 2., 1.]])
比上面代码多加一维,cat拼接效果
X = torch.arange(12, dtype=torch.float32).reshape(1, 3, 4)
Y = torch.tensor([[[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]]])
print(torch.cat((X, Y), dim=0))
print(torch.cat((X, Y), dim=1))
print(torch.cat((X, Y), dim=2))
# tensor([[[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]],
#
# [[ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]]])
# tensor([[[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [ 2., 1., 4., 3.],
# [ 1., 2., 3., 4.],
# [ 4., 3., 2., 1.]]])
# tensor([[[ 0., 1., 2., 3., 2., 1., 4., 3.],
# [ 4., 5., 6., 7., 1., 2., 3., 4.],
# [ 8., 9., 10., 11., 4., 3., 2., 1.]]])
4. 逻辑运算符-构建二元张量
判断每个对应位置的值是否相等,相等则为True–其值为1,不相等则为False–其值为0
print(X == Y)
# tensor([[[False, True, False, True],
# [False, False, False, False],
# [False, False, False, False]]])
5. .sum() 对张量所有元素做求和,会产生一个单元素张量
print((X == Y).sum())
# tensor(2)
6. 广播机制
当运算的两个张量shape不一样的时候,使用从numpy引进的广播机制,最容易出错的地方。
当自己张量相加代码看上去没啥问题,但是总是出错的时候,可以想一下广播机制,是否将张量的形状做了变化。
张量相加的广播机制:把两个张量的形状复制成一样的之后,再对对应位置的元素做相加,比如下面代码会将a的形状复制成(2,3)把b的形状复制成(2,3)之后再对所有元素做对应相加求和。
a = torch.tensor([1, 2, 3.]).reshape(1, 3)
b = torch.tensor([4, 5.]).reshape(2, 1)
print(a)
print(b)
print(a + b)
# tensor([[1., 2., 3.]])
# tensor([[4.],
# [5.]])
# tensor([[5., 6., 7.],
# [6., 7., 8.]])
7. 元素的访问-索引和切片
与Python数组访问方式一样:第一个元素的索引是0,最后一个元素索引是-1; 可以指定范围以包含第一个元素和最后一个之前的元素":"
索引与切片
X = X.reshape(3, 4)
print(X)
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]])
print(X[0]) # 第一维的第0个元素
# tensor([0., 1., 2., 3.])
print(X[-1]) # 第一维的最后一个元素
# tensor([ 8., 9., 10., 11.])
print(X[1:3]) # 第一维的第一个元素到第三个元素 左闭右开区间
# tensor([[ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]])
指定索引赋值
print(X)
X[1, 2] = 9
print(X)
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.]])
# tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 9., 7.],
# [ 8., 9., 10., 11.]])
按区域赋值
“:”代表沿轴1(列)的所有元素
X[1:3, :] = 12
print(X)
# tensor([[ 0., 1., 2., 3.],
# [12., 12., 12., 12.],
# [12., 12., 12., 12.]])
8. 减少内存使用
在内存使用很多的情况下,注意变量不要复制多份,注意内存的使用。
id() 跟c++指针比较类似,获取变量所在的内存位置
print(Y)
# tensor([[[2., 1., 4., 3.],
# [1., 2., 3., 4.],
# [4., 3., 2., 1.]]])
before = id(Y)
print(before)
Y = X + Y
print(id(Y))
# 1481651055168
# 1481651164640
原地更新参数的值 但不改变内存位置
torch.zeros_like(Y) 获得和Yshape一致但是元素值全是0的张量
Z = X + Y 对应元素相加 但是同样会改变张量的内存位置
Z[:] = X + Y 对应元素相加 改变的是Z内的元素值 没有改变张量的内存位置
Z = torch.zeros_like(Y)
print(id(Z))
Z = X + Y
print(id(Z))
print(Z)
Z[:] = X + Y
print(id(Z))
print(Z)
# 1673785960864
# 1673786028976
# tensor([[[ 2., 3., 8., 9.],
# [25., 26., 27., 28.],
# [28., 27., 26., 25.]]])
# 1673786028976
# tensor([[[ 2., 3., 8., 9.],
# [25., 26., 27., 28.],
# [28., 27., 26., 25.]]])
X += 自增 不会改变内存位置
print(X.shape, Y.shape)
Y = Y.reshape((3, 4))
print(id(X))
X += Y
print(id(X))
# torch.Size([3, 4]) torch.Size([1, 3, 4])
# 2013563449888
# 2013563449888
9. 改变数据类型
转为numpy张量(数组)
torch张量和numpy数组将共享它们的底层内存,就地操作更改一个张量也会同时更改另一个张量
A = X.numpy()
B = torch.tensor(A)
print(type(A), type(B))
# <class 'numpy.ndarray'> <class 'torch.Tensor'>
size为1的张量转为python标量
x = torch.tensor([1.0])
print(x, x.item(), float(x), int(x))
# tensor([1.]) 1.0 1.0 1
10. 练习
深度学习存储和操作数据的主要接口是张量(
维数组)。它提供了各种功能,包括基本数学运算、广播、索引、切片、内存节省和转换其他Python对象。
# 1. 运行本节中的代码。将本节中的条件语句X == Y更改为X < Y或X > Y,然后看看你可以得到什么样的张量。
print(X)
print(Y)
print(X==Y)
print(X < Y)
print(X > Y)
# tensor([[ 2., 3., 8., 9.],
# [25., 26., 27., 28.],
# [28., 27., 26., 25.]])
# tensor([[ 2., 2., 6., 6.],
# [13., 14., 15., 16.],
# [16., 15., 14., 13.]])
# tensor([[ True, False, False, False],
# [False, False, False, False],
# [False, False, False, False]])
# tensor([[False, False, False, False],
# [False, False, False, False],
# [False, False, False, False]])
# tensor([[False, True, True, True],
# [ True, True, True, True],
# [ True, True, True, True]])
# 2. 用其他形状(例如三维张量)替换广播机制中按元素操作的两个张量。结果是否与预期相同?
X_3d = torch.tensor([[[1,2]], [[3, 4]]])
print(X_3d.shape)
Y_2d = torch.tensor([[1,2]])
print(Y_2d.shape)
Z = X_3d + Y_2d
print(Z.shape)
print(Z)
# torch.Size([2, 1, 2])
# torch.Size([1, 2])
# torch.Size([2, 1, 2])
# tensor([[[2, 4]],
#
# [[4, 6]]])
3. 数据预处理
课件:https://zh-v2.d2l.ai/chapter_preliminaries/pandas.html
视频:https://www.bilibili.com/video/BV1CV411Y7i4?p=4&spm_id_from=pageDriver&vd_source=eb04c9a33e87ceba9c9a2e5f09752ef8
真实任务的数据是散乱的,不是整理好的张量格式的数据集,所以训练任务的第一步,数据预处理[特征预处理]。
1. 读取csv文件做数据集
真实任务,csv文件也要自己根据任务情况自己做。
csv文件可以参照Excel表格理解,第一行是列名,后面每一行都是一个数据,每一列都叫特征(也叫域)
1. 创建csv文件
os.makedirs('./data', exist_ok=True) # exist_ok=True 即使路径已存在,代码也不会报错
data_file = os.path.join('./data', 'house_tiny.csv')
with open(data_file, 'w', encoding='utf-8')as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
2… 读取csv文件
data_file = os.path.join('./data', 'house_tiny.csv')
data = pd.read_csv(data_file)
print(data)
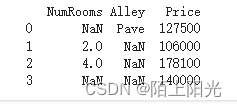
2. 处理缺失值
“NaN”项代表缺失值。 为了处理缺失的数据,典型的方法包括插值法和删除法, 其中插值法用一个替代值弥补缺失值,而删除法则直接忽略缺失值【或者直接删除该行记录】。 在这里,我们将考虑插值法。
1. 缺失值所在列为数值类型
fill 填满 input.fillna(input.mean()) 填充缺失值的方法用输入的均值,适用于列均为数值的
位置索引 iloc 逗号隔开每个维度,每个维度的使用切片取值
input, output = data.iloc[:, :2], data.iloc[:, 2:]
print(input)
print(output)
input = input.fillna(input.mean())
print(input)
NumRooms Alley
0 NaN Pave
1 2.0 NaN
2 4.0 NaN
3 NaN NaN
Price
0 127500
1 106000
2 178100
3 140000
NumRooms Alley
0 3.0 Pave
1 2.0 NaN
2 4.0 NaN
3 3.0 NaN
<ipython-input-8-c801b366d8ba>:3: FutureWarning: The default value of numeric_only in DataFrame.mean is deprecated. In a future version, it will default to False. In addition, specifying 'numeric_only=None' is deprecated. Select only valid columns or specify the value of numeric_only to silence this warning.
input = input.fillna(input.mean())
2. 缺失值所在列为非数值类型
非数值类型无法用均值或者最大最小值等数学计算来代替,可以把一列不同的属性值都当做一个列处理,每列对应位置有对应列名的值则置为1,没有则置为0.
课件解释
对于inputs中的类别值或离散值,我们将“NaN”视为一个类别。 由于“巷子类型”(“Alley”)列只接受两种类型的类别值“Pave”和“NaN”, pandas可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。 巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1,“Alley_nan”的值设置为0。 缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1。
dummies 仿制物 复制列 是pandas的方法不是input的属性
核心代码: pd.get_dummies(input, dummy_na=True)
这个命令是使用Pandas库的get_dummies函数将具有分类变量的输入数据转换成哑变量(虚拟变量),并且设定了dummy_na参数为True。这意味着如果输入数据中包含缺失值(NaN),则会为缺失值创建一个虚拟变量。虚拟变量是一种用于表示分类变量的编码方式,用0和1来表示不同的类别。这个命令可以帮助将分类变量转换为适合建
input = pd.get_dummies(input, dummy_na=True)
print(input)
NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
3. 转为Python张量
dtype=float 默认是64位浮点数,64位浮点数在做模型训练的时候,特征数据很多计算会很慢,可以再转其他数据类型。没有dtype=float64这种写法。
核心代码: torch.tensor(input.to_numpy(dtype=float))
这个命令首先将输入数据转换为NumPy数组,然后将其转换为PyTorch张量。具体来说,首先调用input.to_numpy()方法将Pandas数据框转换为NumPy数组,然后使用dtype=float将NumPy数组的数据类型转换为float,最后使用torch.tensor()函数将NumPy数组转换为PyTorch张量。这个命令的作用是将Pandas数据框转换为PyTorch张量,以便在深度学习模型中使用。
import torch
input = torch.tensor(input.to_numpy(dtype=float))
output = torch.tensor(output.to_numpy(dtype=float))
print(input)
print(output)
tensor([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]], dtype=torch.float64)
tensor([[127500.],
[106000.],
[178100.],
[140000.]], dtype=torch.float64)
4. 练习
1. 删除缺失值最多的列。
代码思路:先统计每行缺失值的个数和,再找到缺失值和最大的那行–该行的序列号,找到后删除即可。
# 1. 删除缺失值最多的列。
data_file = os.path.join('./data', 'house_tiny.csv')
data = pd.read_csv(data_file)
print(data)
missing_counts = data.isnull().sum(axis=1)
print(missing_counts.idxmax())
data = data.drop(missing_counts.idxmax())
print(data)
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
3
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
2. 将预处理后的数据集转换为张量格式。
字符串类型数据无法转成数字格式的张量,将字符串类型的数据根据情况转成数字类型。
# 2. 将预处理后的数据集转换为张量格式。
data = pd.get_dummies(data, dummy_na=True)
data_tensor = torch.tensor(data.to_numpy(float))
print(data_tensor)
tensor([[ nan, 1.2750e+05, 1.0000e+00, 0.0000e+00],
[2.0000e+00, 1.0600e+05, 0.0000e+00, 1.0000e+00],
[4.0000e+00, 1.7810e+05, 0.0000e+00, 1.0000e+00]], dtype=torch.float64)
数据操作QA
1. torch的reshape和view的区别
https://stackoverflow.com/questions/49643225/whats-the-difference-between-reshape-and-view-in-pytorch
view只能作用在连续的张量上(张量中元素的内存地址是连续的)。而reshape连续or非连续都可以。调用x.reshape的时候,如果x在内存中是连续的,那么x.reshape会返回一个view(原地修改,此时内存地址不变),否则就会返回一个新的张量(这时候内存地址变了)。所以推荐的做法是,想要原地修改就直接view,否则就先clone()再改。
但是在pytorch或者numpy中,直接用reshape并不会更改变量的内存地址,相当于数据库中的view使用。
import torch
a = torch.arange(12)
print(a)
b = a.reshape((3,4)) # reshape b并没有复制a,而是创建了一个a的view
print(b)
b[:] = 2 # 在使用过程中尽量不要改数组的值,可能会导致数值不对 一般很少这样操作改值
print(b)
print(a)
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
tensor([[2, 2, 2, 2],
[2, 2, 2, 2],
[2, 2, 2, 2]])
tensor([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
2. 补充学习numpy的使用
3. 快速区分维度
看变量的维度 X.shape 查看X变量的形状
4. torch的tensor和numpy的ndarray相像但不一样
pytorch从torch演化,最早是lua的框架。
mxnet和numpy的api一样。
5. tensor和array的区别
tensor是重载数学上张量的定义,引用到计算机。
array完全是计算机定义的多元数组的概念。n-dimention-array
6. 暂无很好的可视化高维数组的方法
7. 定义完一个变量的内存,后面没有再引用,python会自动释放内存
8. JAX 深度学习框架 可以关注一下
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!