HMM隐马尔可夫模型 评估观察序列概率
隐马尔可夫模型
定义
隐马尔科夫模型(Hidden Markov Model, HMM)是建模序列数据的图模型
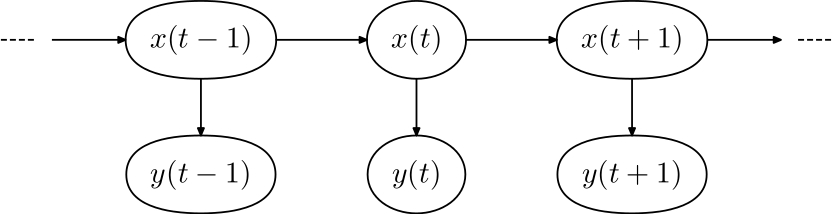
在HMM模型存在隐藏状态 { … , x ( t ? 1 ) , x ( t ) , x ( t + 1 ) , … ? } \{\dots,x(t-1),x(t),x(t+1),\dots\} {…,x(t?1),x(t),x(t+1),…},以及观测状态 { … , y ( t ? 1 ) , y ( t ) , y ( t + 1 ) , … ? } \{\dots,y(t-1),y(t),y(t+1),\dots\} {…,y(t?1),y(t),y(t+1),…}
设
Q
Q
Q为所有隐藏状态的集合,
V
V
V为所有观测状态的集合,即
Q
=
{
q
1
,
q
2
,
…
,
q
N
}
,
V
=
{
v
1
,
v
2
,
…
v
M
}
Q=\{q_1,q_2,\ldots,q_N\},V=\{v_1,v_2,\ldots v_M\}
Q={q1?,q2?,…,qN?},V={v1?,v2?,…vM?}
设存在长度为
T
T
T的序列,其中
I
I
I对应的状态序列,
Q
Q
Q是对应的观察序列
I
=
{
i
1
,
i
2
,
…
,
i
T
}
,
O
=
{
o
1
,
o
2
,
…
o
T
}
i
t
∈
Q
,
o
t
∈
V
I=\{i_1,i_2,\ldots,i_T\},O=\{o_1,o_2,\ldots o_T\}\quad i_t\in Q,o_t\in V
I={i1?,i2?,…,iT?},O={o1?,o2?,…oT?}it?∈Q,ot?∈V
其中HMM满足齐次马尔科夫链假设,即即任意时刻的隐藏状态只依赖于它前一个隐藏状态,一般来说, 给定状态
q
t
q_t
qt?,对于时刻
s
<
t
s<t
s<t 和
t
<
u
t<u
t<u, 则
q
s
q_s
qs?与
q
u
q_u
qu?相互独立。同时满足观测独立性假设。即任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态,即给定状态
q
t
q_t
qt?,对于输出状态
v
s
v_s
vs?与
v
u
v_u
vu?也相互独立
定义在
t
t
t时刻隐藏状态为
i
t
=
q
j
i_t=q_j
it?=qj?到
t
+
1
t+1
t+1时刻隐藏状态为
i
t
+
1
=
q
i
i_{t+1}=q_i
it+1?=qi?的转移概率为
a
i
j
a_{ij}
aij?,即
a
i
j
=
P
(
i
t
+
1
=
q
j
∣
i
t
=
q
i
)
a_{ij}=P(i_{t+1}=q_j|i_t=q_i)
aij?=P(it+1?=qj?∣it?=qi?)
同时
a
i
j
a_{ij}
aij?可以组成马尔科夫链的状态转移矩阵
A
A
A
A
=
[
a
i
j
]
N
×
N
A=\begin{bmatrix}a_{ij}\end{bmatrix}_{N\times N}
A=[aij??]N×N?
定义在
t
t
t时刻隐藏状态为
i
t
=
q
j
i_t=q_j
it?=qj?观测到
o
t
+
1
=
v
k
o_{t+1}=v_k
ot+1?=vk?的概率为
b
j
(
k
)
b_j(k)
bj?(k),即
b
j
(
k
)
=
P
(
o
t
=
v
k
∣
i
t
=
q
j
)
b_j(k)=P(o_t=v_k|i_t=q_j)
bj?(k)=P(ot?=vk?∣it?=qj?)
同时
b
j
(
k
)
b_j(k)
bj?(k)可以组成马尔科夫链的观测概率矩阵
B
B
B
B
=
[
b
j
(
k
)
]
N
×
M
B=\left[b_j(k)\right]_{N\times M}
B=[bj?(k)]N×M?
并定义在
t
=
1
t=1
t=1时刻的隐藏状态概率分布
Π
\Pi
Π
Π
=
[
π
(
i
)
]
N
其中?
π
(
i
)
=
P
(
i
1
=
q
i
)
\Pi=\left[\pi(i)\right]_N\text{其中 }\pi(i)=P(i_1=q_i)
Π=[π(i)]N?其中?π(i)=P(i1?=qi?)
可知一个HMM模型可以由隐藏状态初始概率分布
Π
\Pi
Π , 状态转移概率矩阵
A
A
A 和观测状态概率矩阵
B
B
B 决定。
Π
,
A
\Pi,A
Π,A 决定状态序列,
B
B
B 决定观测序列。因此,HMM模型可以由一个三元组
λ
\lambda
λ表示如下:
λ
=
(
A
,
B
,
Π
)
\lambda=(A,B,\Pi)
λ=(A,B,Π)
直接计算
当给定模型HMM模型 λ = ( A , B , Π ) \lambda=(A,B,\Pi) λ=(A,B,Π)和观测序列 O = { o 1 , o 2 , … o T } O=\{o_1,o_2,\ldots o_T\} O={o1?,o2?,…oT?},求观测序列 O O O在HMM中出现的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)
计算
I
=
{
i
1
,
i
2
,
…
,
i
T
}
I=\{i_1,i_2,\ldots,i_T\}
I={i1?,i2?,…,iT?}出现的概率
P
(
I
∣
λ
)
=
π
i
1
a
i
1
i
2
a
i
2
i
3
?
a
i
T
?
1
i
T
P(I|\lambda)=\pi_{i_1}a_{i_1i_2}a_{i_2i_3}\cdots a_{i_{T-1}i_T}
P(I∣λ)=πi1??ai1?i2??ai2?i3???aiT?1?iT??
其中观测序列
O
=
{
o
1
,
o
2
,
…
o
T
}
O=\{o_1,o_2,\ldots o_T\}
O={o1?,o2?,…oT?}在
I
=
{
i
1
,
i
2
,
…
,
i
T
}
I=\{i_1,i_2,\ldots,i_T\}
I={i1?,i2?,…,iT?}情况下出现的概率
P
(
O
∣
I
,
λ
)
=
b
i
1
(
o
1
)
b
i
2
(
o
2
)
.
…
b
i
T
(
o
T
)
P(O|I,\lambda)=b_{i_1}(o_1)b_{i_2}(o_2).\ldots b_{i_T}(o_T)
P(O∣I,λ)=bi1??(o1?)bi2??(o2?).…biT??(oT?)
根据联合概率公式可得
P
(
O
,
I
∣
λ
)
=
P
(
I
∣
λ
)
P
(
O
∣
I
,
λ
)
=
π
i
1
b
i
1
(
o
1
)
a
i
1
i
2
b
i
2
(
o
2
)
…
a
i
T
?
1
i
T
b
i
T
(
o
T
)
P(O,I|\lambda)=P(I|\lambda)P(O|I,\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)\ldots a_{i_{T-1}i_T}b_{i_T}(o_T)
P(O,I∣λ)=P(I∣λ)P(O∣I,λ)=πi1??bi1??(o1?)ai1?i2??bi2??(o2?)…aiT?1?iT??biT??(oT?)
然后计算边缘概率
P
(
O
∣
λ
)
=
∑
I
P
(
O
,
I
∣
λ
)
=
∑
i
1
,
i
2
,
.
.
,
i
T
π
i
1
b
i
1
(
o
1
)
a
i
1
,
i
2
b
i
2
(
o
2
)
…
a
i
T
?
1
i
T
b
i
T
(
o
T
)
P(O|\lambda)=\sum_{I}P(O,I|\lambda)=\sum_{i_1,i_2,..,i_T}\pi_{i_1}b_{i_1}(o_1)a_{i_1,i_2}b_{i_2}(o_2)\ldots a_{i_{T-1} i_T}b_{i_T}(o_T)
P(O∣λ)=I∑?P(O,I∣λ)=i1?,i2?,..,iT?∑?πi1??bi1??(o1?)ai1?,i2??bi2??(o2?)…aiT?1?iT??biT??(oT?)
虽然直接计算方法有效,但是如果隐藏状态数
N
N
N 非常多,此时预测状态有
N
T
N^T
NT 种组合,算法的时间复杂度是
O
(
T
N
T
)
O(TN^T)
O(TNT) 阶的。因此对于一些隐藏状态数极少的模型,我们可以直接计算来得到观测序列出现的概率,但是如果隐藏状态多,则上述算法太耗时,我们需要寻找其他简洁的算法。
前向计算
前向概率:时刻
t
t
t部分观测序列为
O
=
{
o
1
,
o
2
,
…
o
t
}
O=\{o_1,o_2,\ldots o_t\}
O={o1?,o2?,…ot?} ,且隐藏状态为
q
i
q_i
qi?的概率为
α
t
(
i
)
=
P
(
o
1
,
o
2
,
…
o
t
,
i
t
=
q
i
∣
λ
)
\alpha_{t}(i)=P(o_{1},o_{2},\ldots o_{t},i_{t}=q_{i}|\lambda)
αt?(i)=P(o1?,o2?,…ot?,it?=qi?∣λ)
可得时刻
t
t
t部分观测序列为
O
=
{
o
1
,
o
2
,
…
o
t
}
O=\{o_1,o_2,\ldots o_t\}
O={o1?,o2?,…ot?} ,隐藏状态为
q
j
q_j
qj?且
t
+
1
t+1
t+1时刻隐藏状态为
q
i
q_i
qi?的概率为
α
t
(
j
)
a
j
i
\alpha_{t}(j)a_{ji}
αt?(j)aji?,可推出时刻
t
t
t部分观测序列为
O
=
{
o
1
,
o
2
,
…
o
t
}
O=\{o_1,o_2,\ldots o_t\}
O={o1?,o2?,…ot?} ,且
t
+
1
t+1
t+1时刻隐藏状态为
q
i
q_i
qi?的概率为
∑
j
=
1
N
α
t
(
j
)
a
j
i
\sum_{j=1}^{N}\alpha_{t}(j)a_{ji}
∑j=1N?αt?(j)aji?,若
t
+
1
t+1
t+1时刻的观测状态为
o
t
+
1
o_{t+1}
ot+1?,则可以得到
t
+
1
t+1
t+1时刻观测序列为
O
=
{
o
1
,
o
2
,
…
o
t
+
1
}
O=\{o_1,o_2,\ldots o_{t+1}\}
O={o1?,o2?,…ot+1?}且
t
+
1
t+1
t+1时刻隐藏状态为
q
i
q_i
qi?的概率为:
α
t
+
1
(
i
)
=
[
∑
j
=
1
N
α
t
(
j
)
a
j
i
]
b
i
(
o
t
+
1
)
\alpha_{t+1}\left(i\right)=\left[\sum_{j=1}^{N}\alpha_{t}(j)a_{ji}\right]b_{i}\left(o_{t+1}\right.)
αt+1?(i)=[j=1∑N?αt?(j)aji?]bi?(ot+1?)
由此得到了从前向概率的递推表达式
算法描述
输入:HMM模型
λ
=
(
A
,
B
,
Π
)
\lambda=(A,B,\Pi)
λ=(A,B,Π) ,观测序列
O
=
(
o
1
,
o
2
,
…
o
T
)
O=(o_1,o_2,\ldots o_T)
O=(o1?,o2?,…oT?)
输出:观测序列概率
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ)。
- 初值
α 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , ? ? , N \begin{aligned}\alpha_1(i)=\pi_ib_i(o_1),\quad i=1,2,\cdots,N\end{aligned} α1?(i)=πi?bi?(o1?),i=1,2,?,N?
- 递推 对 t = 1 , 2 , ? ? , T ? 1 t=1,2,\cdots,T-1 t=1,2,?,T?1
α t + 1 ( i ) = [ ∑ j = 1 N α t ( j ) a j i ] b i ( o t + 1 ) , i = 1 , 2 , … , N \alpha_{t+1}\left(i\right)=\left[\sum_{j=1}^{N}\alpha_{t}(j)a_{ji}\right]b_{i}\left(o_{t+1}\right.),\quad i=1,2,\dots,N αt+1?(i)=[j=1∑N?αt?(j)aji?]bi?(ot+1?),i=1,2,…,N
- 终止
P ( O ∣ λ ) = ∑ i = 1 N α T ( i ) P(O|\lambda)=\sum_{i=1}^N\alpha_T(i) P(O∣λ)=i=1∑N?αT?(i)
算法时间复杂度是 O ( T N 2 ) O(TN^2) O(TN2)
后向计算
后向概率:时刻
t
+
1
t+1
t+1到最后时刻
T
T
T的部分观测序列为
{
o
t
+
1
,
o
t
+
2
,
…
o
T
}
\{o_{t+1},o_{t+2},\ldots o_T\}
{ot+1?,ot+2?,…oT?} ,且时刻
t
t
t的隐藏状态为
q
i
q_i
qi?的概率为
β
t
(
i
)
=
P
(
o
t
+
1
,
o
t
+
2
,
…
o
T
∣
i
t
=
q
i
,
λ
)
\beta_{t}(i)=P(o_{t+1},o_{t+2},\ldots o_T|i_{t}=q_{i},\lambda)
βt?(i)=P(ot+1?,ot+2?,…oT?∣it?=qi?,λ)
可得
t
+
2
t+2
t+2到最后时刻
T
T
T观测状态为
{
o
t
+
2
,
o
t
+
3
,
…
o
T
}
\{o_{t+2},o_{t+3},\ldots{o}_T\}
{ot+2?,ot+3?,…oT?},
t
t
t时刻隐藏状态为
q
i
q_i
qi?,
t
+
1
t+1
t+1时刻隐藏状态为
q
j
q_j
qj?的概率为
a
i
j
β
t
+
1
(
j
)
a_{ij}\beta_{t+1}(j)
aij?βt+1?(j),当
t
+
1
t+1
t+1时刻观测到的状态
o
t
+
1
o_{t+1}
ot+1?,此时概率为
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
a_{ij}b_j(o_{t+1})\beta_{t+1}(j)
aij?bj?(ot+1?)βt+1?(j),可得时刻
t
t
t到最后时刻
T
T
T的部分观测序列为
{
o
t
+
1
,
o
t
+
2
,
…
o
T
}
\{o_{t+1},o_{t+2},\ldots o_T\}
{ot+1?,ot+2?,…oT?} ,且时刻
t
t
t的隐藏状态为
q
i
q_i
qi?的概率为
∑
j
=
1
N
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j)
j=1∑N?aij?bj?(ot+1?)βt+1?(j)
算法描述
输入:HMM模型
λ
=
(
A
,
B
,
Π
)
\lambda=(A,B,\Pi)
λ=(A,B,Π) ,观测序列
O
=
(
o
1
,
o
2
,
…
o
T
)
O=(o_1,o_2,\ldots o_T)
O=(o1?,o2?,…oT?)
输出:观测序列概率
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ)
- 初始化时刻 T T T的各个隐藏状态后向概率:
β T ( i ) = 1 , ? i = 1 , 2 , … N \beta_T(i)=1,\:i=1,2,\ldots N βT?(i)=1,i=1,2,…N
- 递推时刻 T ? 1 , T ? 2 , … 1 T-1,T-2,\ldots1 T?1,T?2,…1 时刻的后向概率:
β t ( i ) = ∑ j = 1 N a i j b j ( o t + 1 ) β t + 1 ( j ) , ? i = 1 , 2 , … N \beta_t(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j),\:i=1,2,\ldots N βt?(i)=j=1∑N?aij?bj?(ot+1?)βt+1?(j),i=1,2,…N
- 计算最终结果:
P ( O ∣ λ ) = ∑ i = 1 N π i b i ( o 1 ) β 1 ( i ) P(O|\lambda)=\sum_{i=1}^N\pi_ib_i(o_1)\beta_1(i) P(O∣λ)=i=1∑N?πi?bi?(o1?)β1?(i)
算法时间复杂度是 O ( T N 2 ) O(TN^2) O(TN2)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!