二叉搜索树--二叉排序树

特性

• 搜索依据的关键码，所有节点的关键码互不相同
• 非空左子树的所有键值小于其根结点的键值。
• 非空右子树的所有键值大于其根结点的键值。
• 左、右子树都是二叉搜索树。
• 左 <? 根? < 右，左右都是二叉排序树
• 二叉搜索树-中序遍历从小到大有序

创建二叉搜索树

插入节点：

先判断是否是空树，

判断插入的节点是否存在，存在就不插入，

根据二叉搜索树的性质进行判断是插入左边还是右边

遍历二叉搜索树

编写四个函数，Pre，Next，First，Last。分别表示前驱节点，下一个节点，第一个节点和最后一个节点。

Pre函数，找前驱节点，如果有左子树，则前驱节点是该子树的最后一个节点last，如果没有左子树，判断该节点对于它的父节点来说是否是右孩子（用于判断父节点是否遍历）。

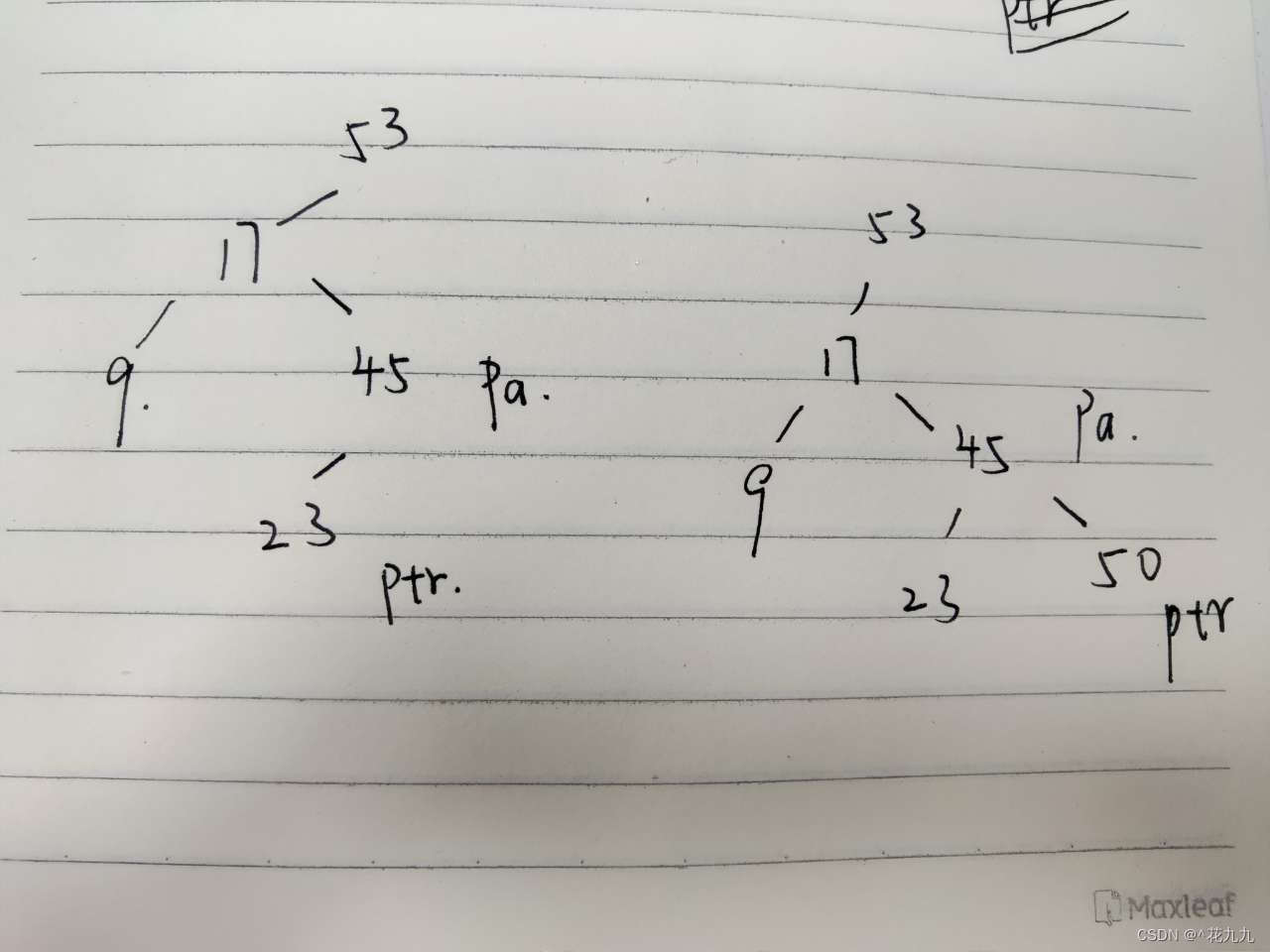
删除节点

删除叶子，删除单分支，删除双分支，删除单分支的根

删除双分支的时候先找到他的直接后继，将直接后继的数据值放到要删的节点位置，将要删的节点删除。

删除单分支的时候，判断时该节点的左孩子还是右孩子，删除该节点后挂到相应的位置。

结构设计

typedef int KeyType;
typedef struct BstNode{
    struct BstNode* leftchild;
    struct BstNode* rightchild;
    struct BstNode* parent;
    KeyType data;
}BSTNode;

typedef struct{
    BstNode* root;
    int cursize;
}BSTree;

void InitTree(BSTree * ptree){
    assert(ptree != nullptr);
    ptree ->cursize = 0;
    ptree->root  = nullptr;
}
BstNode*  FindVal(BSTree* bsptr, KeyType k){
    BstNode * ptr = bsptr->root;
    while(ptr  && ptr->data != k){
        ptr = k < ptr->data ? ptr->leftchild : ptr->rightchild;
    }
    return ptr;
}
BstNode* Search(BstNode* bsptr, KeyType k){
    if(bsptr == nullptr || bsptr->data == k)    return bsptr;
    else if(bsptr->data < k)    return Search(bsptr->rightchild,  k);
    else return Search(bsptr,  k);
}
BstNode *Search_val(BSTree* bsptr, KeyType k){
    return Search(bsptr->root, k);
}
BstNode * BuyNode(){
    BstNode* s = (BstNode *) calloc(1, sizeof(BstNode));
    if(nullptr == s)   exit(EXIT_FAILURE);
    return s;
}
void FreeNode(BstNode * ptr){
    free(ptr);
}

bool Insert_Item(BSTree* ptree, const KeyType kx){
    assert(ptree != nullptr);
    if(ptree -> root == nullptr){
        ptree -> root = BuyNode();
        ptree->cursize = 1;
        ptree ->root->data = kx;
        return true;
    }
    BstNode * ptr = ptree ->root, *pa = nullptr;
    while(ptr != nullptr || ptr ->data != kx){
        pa = ptr;
        ptr = ptr->data > kx ? ptr->leftchild : ptr->rightchild;
    }
    if( ptr != nullptr && ptr->data == kx){
        return false;
    }
    ptr = BuyNode();
    ptr->data = kx;
    ptr->parent = pa;
    if(ptr->data > pa->data){
        pa->rightchild = ptr;
    }
    else{
        pa->leftchild = ptr;
    }
    ptree->cursize += 1;
    return true;

}
void InOrder(BstNode * ptr){
    while(ptr){
        InOrder(ptr->leftchild);
        cout << ptr->data << " ";
        InOrder(ptr->rightchild);
    }
}

void InOrder(BSTree * ptree){
    assert(ptree != nullptr);
    InOrder(ptree->root);
    cout <<endl;

}

BstNode* First(BstNode * ptr){
    while(ptr != nullptr && ptr->leftchild !=nullptr){
        ptr = ptr->leftchild;
    }
    return ptr;
}
BstNode * Last(BstNode * ptr){
    assert(ptr != nullptr) ;
    while(ptr != nullptr && ptr->rightchild != nullptr){
        ptr =ptr->rightchild;
    }
    return ptr;
}

BstNode * Next(BstNode * ptr){
    if(nullptr == ptr)  return nullptr;
    if(ptr->rightchild != nullptr){
        return First(ptr->rightchild);
    }
    else{
        BstNode * pa = ptr->parent;
        while(pa!= nullptr && pa->leftchild != ptr){
            ptr= pa;
            pa = ptr->parent;
        }
        return pa;
    }
}

BstNode* Pre(BstNode * ptr){
    if(nullptr == ptr)  return ptr;
    if(ptr->leftchild != nullptr){
        return Last(ptr->leftchild);
    }
    else{
        BstNode * pa = ptr->parent;
        while(pa != nullptr && pa ->rightchild  != ptr){
            ptr = pa;
            pa = ptr->parent;
        }
        return pa;
    }
}
void ResNIcieOrder(BSTree * ptree){
    assert(ptree != nullptr);
    for(BstNode * ptr = Last(ptree->root); ptr != nullptr; ptr =Pre(ptr)){
        cout << ptr->data <<" ";
    }
    cout << endl;
}
void NiceInOrder(BSTree * ptree){
    assert(ptree != nullptr);
    for(BstNode * ptr = First(ptree->root); ptr != nullptr; ptr = Next(ptr)){
        cout << ptr->data <<" ";
    }
    cout << endl;
}
bool Remove(BSTree * ptree, const KeyType kx){
    assert(ptree != nullptr);
    if(ptree->root == nullptr)    return false;
    BstNode * ptr = FindVal(ptree, kx);
    if(ptr == nullptr)  return false;
    //2leaf
    if(ptr ->leftchild != nullptr && ptr ->rightchild != nullptr){
        BstNode * nextnode = Next(ptr);
        ptr->data= nextnode->data;
        ptr = nextnode;
    } 
    ///oneleaf
    BstNode * child = ptr->leftchild != nullptr ? ptr->leftchild : ptr ->rightchild;
    BstNode * pa = ptr->parent;
    if(child != nullptr)    child->parent = pa;
    if(pa != nullptr){
        if(pa->leftchild == ptr){
            pa->leftchild =child;
        }
        else{
            pa->rightchild = child;
        }
    }
    else{
        ptree->root = child;
    }
    FreeNode(ptr);
    ptree->cursize -= 1;
    return true;
}
int main(){
    BSTree bstree = {0};
    KeyType ar[] = {53, 17,78,9,45,65,87,23,81,94,88};
   
    
    int n = sizeof(ar) / sizeof(ar[0]);
    InitTree(&bstree);
    for(int i = 0; i < n ; ++i){
        Insert_Item(&bstree, ar[i]);

    }
    InOrder(&bstree);
    //NiceInOrder(&bstree);
    //ResNIcieOrder(&bstree);


    KeyType kx;
    
    return 0;
}