Neural axiom network for knowledge graph reasoning 论文精读

原文链接：https://content.iospress.com/articles/semantic-web/sw233276

1.问题的提出

引出当前研究的不足与问题

基于符号和基于embedding的方法。

基于符号的方法，使用预定义的逻辑规则或本体进行KG推理，能够取得较好的性能。

优缺点：虽然这些方法更加可靠和具有人类可解释性，但它们需要丰富的本体（ontologies），而这些本体通常在KG中缺失或不完整。此外，手动定义和维护公理是非常繁琐的。因此，在本文中，论文中探讨了如何编码仅含三元组的隐式公理用于KG推理。
(— 现有方法优缺点 引出本文方法)

基于embedding的方法，如基于翻译的方法、基于语义的方法和神经网络方法等，将实体和关系embedding到低维向量空间中。

优缺点：它们使用向量计算来完成知识图谱，具有可扩展性和高效性。然而，尽管embedding模型取得了成功，但它们主要关注结构信息，而忽略了隐含的公理信息。
(— 现有方法优缺点 引出本文方法)

在本文中，论文中提出了一个用于KG推理的神经公理网络框架NeuRAN。该框架通过知识图谱embedding模型编码显式的结构信息，通过神经网络编码隐式的公理信息。

衡量每个三元组合理性的得分由一个结构信息得分和五个公理信息得分组成。

考虑了五种不同的公理，分别对应于从OWL2本体语言中选取的五种典型的对象属性表达公理，包括ObjectPropertyDomain，ObjectPropertyRange，DisjointObjectProperty，IrreflexiveObjectProperty和AsymmetricObjectProperty

五种公理模块的解释：

定义域和值域限制

ObjectPropertyDomain( :hasWife :Man )

ObjectPropertyRange( :hasWife :Woman )

两个个体通过某个属性相互关联的信息，经常允许推出关于个体本身的进一步结论。特别是可以推断出类成员关系(membership)。

例如，陈述“B是A的妻子”显然隐含着B是女人而A是男人。所以在某种程度上，关于两个个体通过某个属性相关联的陈述，携带着有关这些个体的隐含的额外信息。在论文中的例子中，这些额外信息能够通过类成员关系来表示。OWL提供一种方法说明这种对应关系：

DisjointObjectProperty：

不相交公理模块关注两个关系的语义embedding与同一主客体实体的相容性。

例如，假设已经定义了表示关系hasSpouse和hasParent不相交的公理DissectionObjectProperties (：hasParent：hasSpouse )，那么两个三元组( Linda , hasSpouse , Bruce)和( Linda , hasParent, Bruce))不可能同时正确。原因在于，一个人的配偶不可能是这个人的父母。

IrreflexiveObjectProperty

非自反的公理模块考虑了两个方面的判断。一个是关系(即r是否为非自反的)的性质，另一个是主语和宾语实体是否相等(即s和o是否为同一实体)。因此，只有关系r是非自反的和s = o这两个条件同时满足时，三元组才违背非自反的公理。在OWL2中，一个非自反的关系是指任何实体都不能通过这个非自反的关系与自身相关联。

例如，对于非自反的关系hasParent，直观地说( John , hasParent , John)是一个不正确的三元组。

AsymmetricObjectProperty

非对称公理模块还考虑了两个方面的判断，即关系(即r是否具有不对称性)的性质和给定三元组(即,是否( s , r , o )和( o , r , s)的对称三元组的存在性在同一个KG中都是正确的)。在OWL2中，一个关系是非对称的，即如果它连接了s和o，那么它就不会连接o和s。也就是说，对于正确的三元组( s , r , o)，如果r是非对称关系，且( o , r , s)和( s , r , o)同时出现在同一个KG中，则( o , r , s)违反非对称公理是不正确的。

例如，给定正确的三元组(John、hasChild、David)，我们可以推断(David、hasChild、John)违反了非对称公理，因为hasChild是非对称的。

对于每个公理模块，输出是一个从0到1的概率得分，表示三元组满足公理的程度。该值越接近于1，则该三元组越符合公理。

（—五种公理模块的介绍以及本文模型公理评分介绍）

2.数据来源和模型构建

数据来源

论文中使用两个流行的基准数据集：FB15K237 和WN18RR来评估NeuRAN。

（— 数据来源 ：FB15K237和WN18RR）

论文中基于这两个数据集生成了不同噪声率的新数据集来模拟真实的噪声知识图谱。对于每个数据集，论文中构建了负三元组占正三元组比例分别为10 %、20 %和40 %的3个噪声数据集。

介绍本文中的主要模型与方法

这部分主要介绍模型构建与相关方法

神经公理网络NeuRAN，其中每个三元组的整体得分由来自KGE模块的一个语义得分和来自5个公理模块(即定义域、值域、不相交、非自反的和非对称公理模)的5个公理得分组成。每个公理模块的得分表示该公理成立的概率。假设是这些公理的概率值加强或减轻了三元组存在的概率。因此，三元组( s , r , o)的得分定义为：

较低的E kge表明三元组更可能是正确的较低的( 1-Pdm)，( 1-Prg)，( 1 - Pdis)，( 1-Pir)，( 1 - Pasy)意味着三元组以较高的概率满足相应的神经公理。

论文中在成对得分函数( (即E ( s , r , o ))和E( s′, r′, o′) )上使用基于边际排序损失进行训练，其中γ是一个边缘超参数.损失函数L定义为：

论文中通过随机破坏主语或宾语实体生成负三元组，并确保替换后的三元组在知识图谱中不存在

训练目标是最小化损失函数L来学习公理模块中涉及的实体和关系以及参数的embedding。学习到的embedding和参数被应用于完成下游任务，例如噪声检测，三元组分类和链接预测。

值得一提的是，论文中尝试在模型的设计中引入类型embedding。论文中将类型embedding与语义embedding区分开来。每个实体表示为两个向量(一个类型embedding和一个语义embedding)，每个关系表示为三个向量(两种类型embedding和一种语义embedding)。

符号解释：

以（s,r,o)为例：

s_c : s的类型embedding

o_c : o的类型embedding

s_m : s的语义embedding

o_m : o的语义embedding

r_s : 关系r所期望的主语(s)类型embedding

r_o : 关系r所期望的宾语(o)类型embedding

r_m : 关系r的语义embedding

3.2. KG embedding module

该框架的知识图谱embedding模块涉及一个函数E_kge的学习，该函数旨在根据KGs中的结构信息对每个三元组进行打分。论文中的框架可以使用任意的知识图谱embedding模型作为知识图谱embedding模块。在实验中，论文中以Trans E和Trans H两个embedding模型为例对本文方法进行验证。
（— “Ekge”的学习，用Trans E和Trans H验证）

TransE：

式中：L₁和L₂分别表示L₁和L₂范数。得分函数E_kge的值越小，表示三元组正确的概率越高。

TransH：

其中投影

.它限制
如果( s , r , o)成立，则得分较低，否则得分较高。

3.3. Five axiom modules

公理模块的设计依赖于这些公理的定义。

具体来说，对于领域/范围公理，论文中使用关系r_s / r_o所期望的主观/客观实体的类型embedding和主观/客观实体s_c / o_c的类型embedding来计算类型兼容性得分。

3.3.1. Domain axiom module

3.3.2. Range axiom module

3.3.3. Disjoint axiom module

对于不相交公理，论文中探讨了任意两个具有相同主客体实体的关系的语义相容性。

论文中假设( om-sm)表示主语为s和宾语为o的关系的共享语义embedding。然后计算rm和( om-sm)的相似度得分，以反映不相交公理的满足程度。

3.3.4. Irreflexive axiom module

对于非自反的公理，考虑关系是否为非自反的，主体实体是否与客体实体( s = o ?)相同。

非自反的公理模块考虑了两个方面的判断。一个是关系(即r是否为非自反的)的性质，另一个是主语和宾语实体是否相等(即s和o是否为同一实体)。只有关系r是非自反的和s = o这两个条件同时满足时，三元组才违背非自反的公理。

其中g( x , y)是一个函数，且g( x , y) = abs( x-y) . W₁∈R^1×(dm+tm)，d_m和t_m分别表示语义embedding和类型embedding的维数，σ表示Sigmoid函数. [ ;]表示级联操作。

3.3.5. Asymmetric axiom module

对于非对称公理，关注关系是否非对称，输入三元组的对称三元组是否存在( ( o , r , s)∈G ? )。然后论文中详细介绍了这些典型的公理。

非对称公理模块还考虑了两个方面的判断，即关系(即r是否具有不对称性)的性质

和给定三元组(即,是否( s , r , o )和( o , r , s)的对称三元组的存在性在同一个KG中都是正确的)。

考虑r_s和r_o的相容性。其原因在于，如果r是对称的，论文中可以从观测中推断r_s≈r_o，从三重( s , r , o)中推断r_s≈s_c，r_o≈o_c，从三重( o , r , s)中推断r_s≈o_c，r_o≈s_c。

TransE检验( o , r , s)是否存在

（— 关于5种公理的实现原理）

关于SIGMOID函数：

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid函数为神经网络中的激励函数，是一种光滑且严格单调的饱和函数，其表达式为：

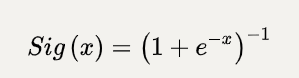
该饱和函数的上、下界为（0,1）。

具有以下优缺点：

优点：平滑、易于求导。

缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

3.结果分析

讲本文中的模型与方法的结果对比其他方法的优势与不足，分析原因

论文中在三个主要的知识图谱推理任务上评估了论文中提出的方法NeuRAN：噪声检测、链接预测和三元组分类。

baseline：论文中选择TransE或TransH作为知识图谱embedding模块，并将论文中的方法(即NeuRAN ( TransE ))，NeuRAN ( TransH ) )与它们进行比较。论文中还考虑了CKRL ( TransE )和CKRL ( TransH )作为基线，它们在噪声知识图谱中为知识图谱推理引入了路径信息。

4.2. Noise detection

噪声检测

它的目的是根据三元组的得分来检测噪声KGs中可能存在的噪声，并将其视为训练集上的三元组分类任务。

E(s, r, o) = E_kge + λ ·[(1 ? P_dm) + (1 ? P_rg) + (1 ? P_dis) + (1 ? P_irr) + (1 ? P_asy)]计算三元组( s , r , o)的得分。

**三元组得分越低，则该三元组越有效。**能量函数值较高的三元组往往是噪声。论文中考虑评价指标ROC曲线下面积( auc值)，以检查该方法将噪声分类为错误的程度。在计算AUC指标之前，论文中将能量函数得分归一化到[ 0、1 ]区间。接近0的值表示正确的三元组，接近1的值表示错误的三元组。

(1) 论文中的模型在WN18RR - 10 %，WN18RR-20 %，FB15K237上表现与TransE、CKRL(TransE)、TransH和CKRL(TransH)相当或略优。

(2) 在TransH中，在基于WN18RR和FB15K237的数据集上，基于公理信息的模型在噪声检测上的性能优于基于路径信息的模型。

(3) 随着噪声增加，在基于WN18RR的数据集上，基线和论文中的模型的噪声检测能力下降；而在基于FB15K237的数据集上可能增加，这表明噪声数据集中的关系和三元组越多，即使这些三元组可能是噪声也可能会引入更多的有效信息。

因此，我们可以得出结论，隐式公理信息有助于噪声检测，并且在具有大量关系和三元组的数据集上得到更好的体现。

4.3. Triple classification

三元组分类

E(s, r, o) = E_kge + λ ·[(1 ? P_dm) + (1 ? P_rg) + (1 ? P_dis) + (1 ? P_irr) + (1 ? P_asy)]计算三元组( s , r , o)的得分来判断测试集中的某个三元组是否正确，可以看作是测试集上的二分类任务

论文中通过随机破坏正确三元组的主语或宾语实体来生成负三元组。

对于三元组分类，论文中为每个关系学习一个关系特定的阈值δ r，δ r通过最大化验证集上的分类精度来优化。给定一个三元组( s , r , o)，如果能量函数得到的得分低于δ r，则将其分类为正，否则为负。论文中使用准确率( ACC )、精确率( P )和召回率( R )作为评价指标。

（— 三元组分类任务方法与评估指标）

(1) 在三个指标中，论文中的方法在基于WN18RR的数据集上优于基线，取得了最佳结果，证实了利用公理信息学习知识表示有助于三元组分类。

(2) 在基于FB15K237的数据集上，结果与基线具有可比性。在基于WN18RR的数据集上相较于在基于FB15K237的数据集上的改善更为明显，表明在关系和三元组数量较少的数据集上，隐式公理信息更为有效。

(3) 与TransE、TransH、CKRL(TransE)和CKRL(TransH)相比，噪声率越高，论文中的方法在基于WN18RR的数据集上的精度下降较小。这表明在噪声数据集上，NeuRAN的三分类结果比小数据集上的基线更加鲁棒。

从三元组分类结果可以得出，在关系和三元组数量较少的数据集上，结合知识图谱中已有三元组所反映的隐含公理和结构信息比仅使用结构信息效果更好。

（— 三元组分类任务实验结果分析与结论）

4.4. Link prediction

论文中进行了链接预测来评估知识图谱补全的性能。该任务旨在预测给定三元组的一个实体和一个关系时缺失的实体，包括主题实体预测( ? , r , o)和对象实体预测( s , r , ?)。

对于每个测试三元组，假设主题实体预测( ? , r , o)与正确的主题实体s。论文中首先将数据集中所有的实体e∈E作为候选预测，然后用每个实体e替换缺失的部分，并计算T = { ( e、r、o) | e∈G }中三元组的得分。随后，论文中对这些得分进行升序排列，并存储正确实体的排名。对象实体预测也是如此。评价指标为MRR和Hits @ N，其中MRR是所有测试三元组的秩的平均倒数秩，Hits @ N ( N = 1 , 3)是所有测试三元组中秩在N以内的比例。

(1) 在基于WN18RR的数据集上相较于在基于FB15K237的数据集上，论文中的方法的链接预测结果较基线有提升，证实了学习到的知识图谱embedding质量更好，对完成KGs有帮助。在噪声数据集上，公理信息比路径信息更有用。

(2) 在基于WN18RR的数据集上，论文中的方法在所有指标上都取得了最佳性能，尤其在Hits @ 1指标上的显著改进表明公理信息在关系和三元组较少的数据集中有助于提高缺失三元组的预测能力。

(3) 在基于FB15K237的数据集上，虽然改进相对于基于WN18RR的数据集并不显著，但仍优于基线。这再次证实论文中的方法能够提高链接预测，尤其在关系和三元组较多的情况下，公理信息的优势更为明显。

因此，我们可以得出结论，由神经公理网络编码的隐式公理信息有助于提高实体和关系的embedding学习质量和链接预测结果。而且，这种信息在关系和三元组相对较少的数据集上更加有效。

（— 链接预测任务实验结果分析与结论）

4.5. Ablation study

消融实验

论文中对链路预测进行消融研究，以评估NeuRAN的有效性。论文中将每个公理模块添加到知识图谱embedding模块中，以考察公理模块的贡献。

E(s, r, o) = E_kge + λ · E_a

从结果可以看出添加公理模块后与不添加公理模块时的相比，在链接预测任务中部分公理模块的结果相当，添加部分模块的有较明显的优化。

不相交模块和非自反的模块的工作效果优于其他模块，虽然领域模块、范围模块和非对称模块的效率不如其他模块，但综合五个模块的效率有较为明显的提升。

（— 对链接预测进行消融实验评估加入每个公理模块的有效性）

4.结论与启示

总结全文得出结论，提炼亮点与启示

在本文中，论文中提出了一种新的神经公理网络模型，旨在对噪声知识图谱进行推理。论文中不仅考虑编码三元组的结构信息，而且考虑编码三元组的公理信息。具体来说，论文中提出了一个用于保留结构的知识图谱embedding模块和五个不同的公理模块，用于计算满足相应公理的概率得分。论文中在KG噪声检测、三元组分类和链接预测上对论文中的方法进行了评估。实验表明，公理信息可以使这些任务受益。

主要贡献：

主要贡献总结如下：

• 论文中提出了神经公理学习问题，其中公理信息不是给定的，而是可以通过KG中现有的三元组来反映和学习的。

• 论文中提出了一个框架NeuRAN，该框架使用一个知识图谱embedding模块和五个公理模块分别编码显式的结构信息和隐式的公理信息。

• 论文中在具有不同噪声比率的数据集上对NeuRAN进行了评估。实验结果证明了论文中的方法在知识图谱推理上的有效性。

（— 主要贡献总结）