基于模型驱动的可解释性全色、多光谱、高光谱融合网络

摘要

摘要:同时融合高光谱(HS)、多光谱(MS)和全色(PAN)图像为生成高分辨率HS (HRHS)图像提供了一种新的范式。在这项研究中，我们提出了一个可解释的模型驱动的深度网络，用于HS, MS和PAN图像融合，称为HMPNet。我们首先提出了一种新的融合模型，该模型在描述HRHS和PAN图像之间由于分辨率差异大而导致的复杂关系之前利用了深度。
因此，传统的基于模型的方法在设计合适的手工先验时的困难可以缓解，因为这种深度先验是从数据中学习的。通过一系列的迭代步骤，我们进一步解决了基于近端梯度下降(PGD)算法的融合模型的优化问题。

通过将这些迭代步骤展开到几个网络模块中，我们最终得到了HMPNet。因此，除了深度先验之外的所有参数都在深度网络中学习，简化了融合过程中最优参数的选择，实现了空间质量和光谱质量之间的良好平衡。

同时，HMPNet中包含的所有模块都具有可解释的物理意义，提高了其泛化能力。在实验中，我们从视觉比较和定量分析方面展示了HMPNet相对于其他最先进方法的优势，其中使用了一系列模拟和真实数据集进行验证。

介绍

高光谱(HS)图像具有数百个连续光谱波段，已广泛应用于环境监测、农业分析和场景解释等众多应用中。虽然高分辨率图像的光谱信息丰富，但由于光学传感器接收到的能量有限，其空间分辨率相对较低，相反，多光谱(MS)或全色(PAN)图像通常具有较高的空间分辨率，但光谱带较少。因此，将HS图像与MS图像(或PAN图像)融合生成高空间分辨率的融合HS图像是很直观的，本研究称之为HSI融合。

受深度学习(DL)在不同计算机视觉和图像恢复应用中的一系列突破的启发，深度卷积网络已应用于HSI融合。现有的基于dl的HSI融合方法主要集中在HS和MS图像的融合(FHM)上。传统的基于dl的FHM方法将cnn与专门设计的先验相结合，以增强深度融合模型的适应性。Palsson等人[1]提出了一种深度FHM方法，该方法利用主成分分析来降低融合的维数。之后，Dian等[2]通过残差学习学习先验，实现了FHM问题的正则化。Xie等[3]联合利用观测模型和中间MS图像的低秩先验约束，构建了一个创新的深度网络MHF-Net。Qu等[4]，[5]首先尝试使用无监督编码器-解码器架构来解决FHM问题，并进一步考虑了不同模态的未注册问题。考虑到空间-光谱融合问题，[6]研究了基于DenseNet的残差高密度网络。由于在实践中图像的退化总是未知的，Zhang等[7]为“盲”FHM引入了一种无监督的深度框架。

Wang等人[8]也进行了类似的无监督研究，使用了非线性变分概率生成模型。为了进一步提高融合后HS图像的空间分辨率，HS与PAN图像的融合(FHP)是一个很好的选择，因为PAN图像总是比MS图像提供更高的空间分辨率。例如，He等[9]引入了一种基于频谱预测卷积神经网络的HyperPNN来融合HS图像和PAN图像。随后，Dong等人[10]利用带有两个鉴别器的生成对抗网络开发了一个FHP任务。

尽管已经有相当多的FHM和FHP方法专门用于解决HSI融合任务，但由于以下原因，生成具有高空间和光谱质量的融合HS图像仍然具有挑战性。1)融合后的HS图像的空间质量由于MS图像的空间分辨率不高，FHM仍然不能令人满意;2)由于HS图像和PAN图像的光谱分辨率差异较大，FHP总是存在明显的光谱失真。

最近，HS、MS和PAN图像的融合(FHMP)[11]为HSI融合带来了更好地平衡空间和光谱质量的新见解，如图1所示。

然而，这种FHMP方法被训练成一个黑盒，忽略了融合过程的真实物理意义。

因此容易出现过拟合，泛化能力较低。因此，它的性能与训练样本和测试样本之间的一致性高度相关。

为了解决上述棘手的问题，本研究引入了一个可解释的模型驱动深度网络HMPNet，以增强基于dl的FHMP的泛化能力。我们首先建议利用可以从数据中学习的深度先验来描述HS图像和PAN图像之间的潜在关系。

这有助于提高融合模型的精度。通过进一步合并将HS图像和MS图像分别作为融合后HS图像的空间和频谱退化结果的两个数据保真度项，我们得到了本研究所需的融合模型。为了解决该融合模型的优化问题，我们采用了近端梯度下降(PGD)算法，将其求解转化为多个迭代步骤。最后，我们通过将上述迭代步骤展开到几个深度网络模块来构建HMPNet。因此，对所有属于融合模型的参数进行了优化，并从数据中学习，提高了融合性能。同时，HMPNet中包含的所有模块都具有不同的物理含义，使得网络具有良好的泛化能力。

我们将本研究的主要贡献总结如下。

1)采用融合后的HS和PAN图像之间的深度先验，构建新的FHMP融合模型。

与传统的手工先验不同，这种深度先验是从数据中学习的，从而提高了融合模型的准确性。

2)我们提出了一种可解释的模型驱动深度网络来解决该融合模型的优化问题，从而在空间质量和光谱质量之间取得了良好的平衡。具体来说，这个深度网络的每个模块都与优化问题的解的迭代步骤相关。因此，所提出的深度网络具有明确的物理意义，提高了其泛化能力。

3)除了模拟实验外，还利用高分(GF)系列(即GF-5和GF-1)卫星图像融合的真实实验，展示了HMPNet相对于其他最先进方法的优势。

我们将本文的其余部分组织如下。第二节介绍了相关工作，第三节详细描述了拟议的HMPNet。我们在第四节给出实验结果，在第五节报告结论。

相关工作

在本节中，我们将简要介绍除基于dl的HS图像融合方法外，传统FHM、FHP、FHMP方法的相关工作。

传统的FHM方法可分为三大类:扩展泛锐化方法、基于矩阵分解的方法和基于张量分解的方法。与FHM相比，融合MS和PAN图像的pansharpening[12]，[13]，[14]得到了广泛的研究。

一些泛锐化方法的扩展可以直接用于FHM。例如，Selva等[15]将MS图像的空间细节直接注入到HS图像中，生成了融合HS图像。基于矩阵分解的方法将期望的HS图像分解成具有光谱基的系数，该方法假设每个像素是由一些光谱原子线性组合而成。Kawakami等[16]将融合任务视为解混问题，并将其转化为将输入分解为一组稀疏系数和一个基的搜索。Simoes等[17]采用保边正则化器，将融合问题表述为一个特殊凸目标函数的最小化。Akhtar等[18]，[19]提出了一种基于稀疏表示和字典学习的FHM方法，并在贝叶斯框架中进一步实现。Wei等人[20]提出了一种基于变分的融合HS图像和MS图像的方法，其中精心设计了基于一组字典的稀疏正则化项。Lin等[21]在距离平方和正则化器之外，提出了耦合非负矩阵分解(CNMF)，交替更新谱基和系数，具有良好的融合性能。基于张量分解的方法从张量的角度解决融合任务，因为HS图像可以自然地表示为三维张量[22]。Li等人

[23]创新性地对HS图像和MS图像进行稀疏张量分解，并进一步利用一对稀疏张量分解算法进行融合。为了提高融合性能，进一步研究了基于子空间的低张量多秩正则化[24]。Chang等[25]通过对不同稀疏度正则化参数的核心张量进行约束，提出了一种基于加权低秩张量恢复的FHM新方法。Xu等[26]设计了一个统一的框架，将非局部相似度、张量字典学习和稀疏编码融合到HS图像和MS图像中，很好地保留了非局部相似块之间的光谱和空间相似性。

此外，为了捕获的高阶相关性HS图像中，[27]提出了FHM的高阶耦合张量环表示，其中采用图拉普拉斯正则化来保持光谱信息。

尽管近几十年来已经研究了相当多的FHM方法，但由于MS图像的空间分辨率仍然很低，融合HS图像的空间质量仍然令人不满意。

一般来说，现有的FHP方法主要来源于泛锐化方法，可分为三大类:组件替代(CS)、多分辨率分析(MRA)和基于模型的方法。CS方法将HS(或MS)图像的空间分量替换为PAN图像，从而生成具有高空间质量的融合HS (MS)图像。例如，作为一种常见的CS方法，gram-Schmidt adaptive (GSA)[28]可以直接应用于FHP。Licciardi等[29]提出采用替代和注入相结合的混合算法求解FHP。为了在MRA方法中将PAN图像的空间细节注入到HS图像中，使用了各种多尺度分解方法，如抽取小波变换[30]、基于平滑滤波器的强度调制[31]和具有广义拉普拉斯金字塔(GLP)的调制传递函数[32]。近年来，基于模型的方法得到了广泛的研究，该方法基于不同物理观测的融合模型，与CS和MRA方法相比，可以更好地平衡空间和光谱质量。一般来说，由于HS图像与PAN图像的光谱(或空间)分辨率差异较大，FHP方法的光谱失真往往比FHM方法更严重。

最近，在FHMP方法中只有少数几种方法被研究。CNMF在[33]中首次应用于FHMP任务。Bendoumi和Benlefki[34]进一步提出了一种基于CNMF的解混融合框架，但其辅助变量的初始化严重影响期望融合的HS图像解析解的精度。Arablouei[35]通过估计融合HS图像计算的端元及其丰度来解决FHMP任务。Tian等人[36]提出了一种新的计算范式，利用HS图像的低秩特性以及PAN和MS图像之间的梯度相似性来实施正则化先验。一般来说，这些方法在设计手工参数和先验约束方面存在不可避免的困难，从而限制了融合性能。最近，深度学习在[11]中首次被用于解决FHMP任务，称为HyperNet。通过对数据的学习，可以获得较好的融合效果。然而，HyperNet是作为一个没有明确物理含义的黑盒子来学习的。因此，其泛化能力还不高。

提出的模型

A. Proposed FHMP Model

在本研究中，我们特别考虑了FHMP任务。为了在我们的研究中简化下面的描述，我们重塑以下是将引号中的公式使用 LaTeX 格式进行渲染：

我们以波段的形式表示HS、MS和PAN图像，分别构建了矩阵 $L_h\times W_h{H}_h$，$L_m\times W_m{H}_m$ 和 $1\times W_p{H}_p$。特别是，HS图像包含 $L_h$个波段，每个波段包含 $W_h\times H_h$个像素。MS的每个波段的大小是$W_m\times H_m$，PAN的大小是 $W_p\times H_p$。从物理观测上考虑，我们将HS图像视为模糊和降采样的HS图像的一个版本。同时，我们将MS图像视为融合HS图像的经过模糊和空间-光谱降采样后的版本。因此，与HS、MS和融合HS图像相关的物理关系可以描述如下：

$$\begin{gathered} Y_h=X{B}_h{S}_h \\ {Y}_m=R_{m}X{B}_m{S}_m \end{gathered}$$

其中变量解释如下：

1. $X\in {\mathbb{R}}^{L_h\times W_p{H}_p}$是融合的HS图像，具有$L_h$ 个波段，每个波段有 $W_p,H_p$个像素。
2. $Y_h\in {\mathbb{R}}^{L_h\times W_h{H}_h}$和 $Y_m\in {\mathbb{R}}^{L_m\times W_m{H}_m}$分别代表观测到的HS和MS图像。
3. $B_h\in {\mathbb{R}}^{W_p{H}_p\times W_p{H}_p}$和 $B_m\in {\mathbb{R}}^{W_p{H}_p\times W_m,H_m}$表示对波段进行循环卷积操作的操作符。
4. $S_h\in {\mathbb{R}}^{W_p{H}_p\times W_h{H}_h}$和 $S_m\in {\mathbb{R}}^{W_p{H}_p\times W_m{H}_m}$ 是降采样矩阵。
5. $R_m\in {\mathbb{R}}^{L_m\times L_h}$表示MS传感器的光谱响应。

因此，我们可以通过以下图像保真度项来表述上述关系：

$$\arg \underset{\mathbf{X}}{\min }\frac{1}{2}\Vert {\mathbf{Y}}_h?\mathbf{X}{\mathbf{B}}_h{\mathbf{S}}_h{\Vert }_F^2+\frac{{\lambda }_m}{2}\Vert {\mathbf{Y}}_m?{\mathbf{R}}_m\mathbf{X}{\mathbf{B}}_m{\mathbf{S}}_m{\Vert }_F^2$$

其中${\lambda }_m$是用来平衡不同项的参数。为了将全色图像 $Y_p\in {\mathbb{R}}^{1\times W_p,H_p}$的空间细节转移到融合图像 $X$ 中，一个先验项对于描述它们之间的关系至关重要。我们使用以下实验来演示，采用了配准的全色和高分辨率高光谱（HRHS）图像。我们主要分析全色图像与HRHS图像中一个波段之间的分布差异，如图2所示。与图2(a)中通过强度评估的分布差异相比，通过高频操作符如梯度评估的分布差异在图2(b)中更便于数学描述。例如，群梯度稀疏性在文献[36]中被采用作为梯度相似性的先验描述。然而，这种手工先验仍然是不准确的，因为自然场景的特征是复杂的。

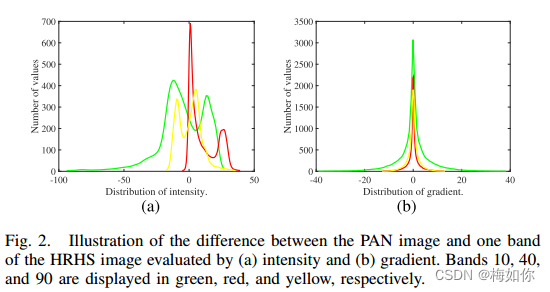
Fig2 通过(a)强度和(b)梯度评估PAN图像和HRHS图像的一个波段之间的差异。波段10、40和90分别以绿色、红色和黄色显示。

同时，每个HRHS图像的波段与PAN图像具有不同的相似度，因此不适合对每个波段进行相同的固定先验。例如，图2(b)中波段10(绿色曲线)的分布与波段40(红色曲线)或波段90(黄色曲线)的分布偏差较大。利用深度神经网络在自然场景图像统计方面的强大能力，我们提出学习$Y_p$和$X$残差知识的深度先验:
$$\mathbf{\Psi }({\mathbf{R}}_p\mathbf{X}?{\mathbf{Y}}_p)$$

其中${\mathbf{R}}_p\in {\mathbb{R}}^{1\times L_h}$ 代表 PAN 图像的光谱响应矩阵.

结合(3)(4)，提出的模型可以表示为:

其中 ${\lambda }_p$ 是另一个平衡参数。
B. 优化过程

我们使用高效的PGD算法[37]，[38]来求解（5），它包括两个保真度项（1/2）$\Vert Y_h?X{B}_h{S}_h{\Vert }_2^2$（可微分部分，表示为f(X)）和深度先验$\rho (R_{p}X?Y_p)$（不可微分部分），如下所示：
$$\{\begin{array}{l}{\mathbf{Z}}^{t+1}={\mathbf{X}}^t?\mu {▽}_{\mathbf{X}}f(\mathbf{X})\\ {\mathbf{X}}^{t+1}=\arg {\min }_{\mathbf{X}}\frac{1}{2}\Vert \mathbf{X}?{\mathbf{Z}}^{t+1}{\Vert }_F^2+{\hat{\lambda }}_p\Psi ({\mathbf{R}}_p\mathbf{X}?{\mathbf{Y}}_p)\end{array}$$

其中，

$${?}_{X}f(X)=(X{B}_h{S}_h?Y_h)S_h^T{B}_h^T+{\lambda }_m{R}_m^T(R_{m}X{B}_m{S}_m?Y_m)S_m^T{B}_m^T(8)$$

在（7）中，${\hat{\lambda }}_p=\mu {\lambda }_p$,

每次迭代中的$Z_{t+1}$可以被视为$X_{t+1}$的中间结果。因此，从图像逆问题的角度来看，自然地假设$X_{t+1}$和$Z_{t+1}$之间的残差服从均值为零、方差为${\delta }^2$的正态分布[39]。根据[40]的类似推导，可以将（7）重写如下：

$$X_{t+1}={\text{arg?min}}_X\frac{1}{2\tau }\Vert R_{p}X?R_p{Z}_{t+1}{\Vert }_2^{2}F+{\hat{\lambda }}_p\rho (R_{p}X?Y_p)(9)$$

其中，$\tau$是与$R_p$相关的标量。

我们假设$V=R_{p}X?Y_p$，则有

$$V_{t+1}={\text{arg?min}}_V\frac{1}{2\tau }\Vert V?(R_p{Z}_{t+1}?Y_p){\Vert }_2^{2}F+{\hat{\lambda }}_p\rho (V)(10)$$

（10）的形式类似于去噪问题[41]，[42]，可以通过本文第III-C节介绍的现有深度架构有效地解决。

然后，我们可以得到$X$的近似解如下：

$$X_{t+1}=\widehat{R_p}(V_{t+1}+Y_p)(11)$$

其中，$\widehat{R_p}$是$R_p$的伪逆。

最后，根据上述分析，我们总结了算法1的完整步骤。通过将算法1的优化步骤展开成几个网络模块，我们构建了HMPNet，如图3所示。特别地，HMPNet的第$t$阶段对应于算法1的第$$t$$次迭代。每个阶段中的保真度模块$F(?,?,?,?,?)$和深度先验模块$D(?,?,?)$是基于$Z$和$X$的解决方案设计的。