08、基于LunarLander登陆器的DDQN强化学习(含PYTHON工程)
08、基于LunarLander登陆器的DDQN强化学习(含PYTHON工程)
LunarLander复现:
07、基于LunarLander登陆器的DQN强化学习案例(含PYTHON工程)
08、基于LunarLander登陆器的DDQN强化学习(含PYTHON工程)
0、实践背景
gym的LunarLander是一个用于强化学习的经典环境。在这个环境中,智能体(agent)需要控制一个航天器在月球表面上着陆。航天器的动作包括向上推进、不进行任何操作、向左推进或向右推进。环境的状态包括航天器的位置、速度、方向、是否接触到地面或月球上空等。
智能体的任务是在一定的时间内通过选择正确的动作使航天器安全着陆,并且尽可能地消耗较少的燃料。如果航天器着陆时速度过快或者与地面碰撞,任务就会失败。智能体需要通过不断地尝试和学习来选择最优的动作序列,以完成这个任务。
下面是训练的结果:
1、DDQN (Double DQN)实现原理
参考:DeepRL系列(8): Double DQN(DDQN)原理与实现
论文地址:https://arxiv.org/pdf/1509.06461.pdf
在Q-learning学习中“过估计”是经常发生的,并且影响实验的性能。具体来讲,Q-learning和DQN算法往往会过高估计Q值。
这个过估计来自于max函数,也就是贝尔曼方程:
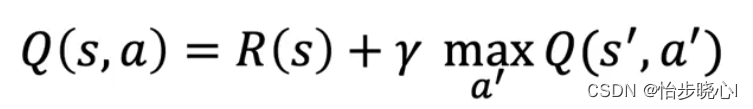
基于LunarLander登陆器的DQN强化学习案例(含PYTHON工程)中讲到,max(Q(s’,a’))的获取完全依赖与Target Q网络,相当于一家独大,说啥就是啥,因此容易造成Q值的“过估计”。
2010年作者Hasselt就针对过高估计Q值的问题提出了Double Q-learning,他就是尝试通过将选择动作和评估动作分割开来避免过高估计的问题。这意味着我们仍然使用贪心策略去学习估计Q值,而使用第二组权重参数去评估其策略,相当于鸡蛋不放在一个篮子里。
Double DQN就是为了解决DQN的高估问题,采用类似的思想,鸡蛋不放在一个篮子里。具体来讲,高估是因为max函数,也就是max(Q(s’,a’)),这个函数的值全权取决于Target Q网络。然而,在DQN算法中,存在Q网络和Target Q两个网络,我们可以采用Q网络去得到s’状态下各个动作的动作价值函数,从而计算应该采取最优动作a。随后,使用Target Q网络计算Q值,选取依赖于Q网络得到的动作a作为最优动作,而不是直接进行max取最大值。
例如,有三个离散动作,其对应的Target Q网络的输出是[0.2,0.3,0.4],在DQN中,我们max(Q(s’,a’))依赖于Target Q网络,那么max(Q(s’,a’))的值就是第3个动作的值0.4。然而,对于DDQN,假设Target Q网络的输出是[0.2,0.3,0.4],但是当前状态下Q网络的输出是[0.2,0.4,0.3],我们就会知道对于Q网络动作2是最优的,如何就会从Target Q网络的输出中取第二个值作为输出,也就是输出0.3。
2、DDQN 和DQN实现代码对比
基于LunarLander登陆器的DQN强化学习案例(含PYTHON工程)已经给出了DQN的全部实现代码,网络构建方面全部相同,只是在loss计算有所不同:
# 获取q_values
q_values = q_network(states)
if self.model == 'DQN':
# 计算最大的Q^(s,a),reduce_max用于求最大值
max_qsa = tf.reduce_max(target_q_network(next_states), axis=-1)
# 如果完成,设置y = R,否则设置y = R + γ max Q^(s,a)。
y_targets = rewards + (gamma * max_qsa * (1 - done_vals))
elif self.model == 'Double_DQN':
# 从Q网络得出最优动作的index_Q
next_action = np.argmax(q_values, axis=1)
# tf.range(q_values.shape[0]构建0-batch_size的数组,next_action是q_network得出的动作,两者组合成二维数组
# 从target_q_network(next_states)输出的batch_size*action dim个数组中取数
# 从从target_q_network中取出index_Q(来自Q网络)位置的Q值作为输出
Q2 = tf.gather_nd(target_q_network(next_states),
tf.stack([tf.range(q_values.shape[0]), tf.cast(next_action, tf.int32)], axis=1))
y_targets = rewards + (gamma * Q2 * (1 - done_vals))
全部的Loss计算函数:
def compute_loss(self, experiences, gamma, q_network, target_q_network):
"""
计算损失函数。
参数:
experiences: 一个包含["state", "action", "reward", "next_state", "done"]的namedtuples的元组
gamma: (浮点数) 折扣因子。
q_network: (tf.keras.Sequential) 用于预测q_values的Keras模型
target_q_network: (tf.keras.Sequential) 用于预测目标的Keras模型
返回:
loss: (TensorFlow Tensor(shape=(0,), dtype=int32)) y目标与Q(s,a)值之间的均方误差。
"""
# 获取数据
states, actions, rewards, next_states, done_vals = experiences
# 获取q_values
q_values = q_network(states)
if self.model == 'DQN' or self.model == 'Dueling_DQN':
# 计算最大的Q^(s,a),reduce_max用于求最大值
max_qsa = tf.reduce_max(target_q_network(next_states), axis=-1)
# 如果登录完成,设置y = R,否则设置y = R + γ max Q^(s,a)。
y_targets = rewards + (gamma * max_qsa * (1 - done_vals))
elif self.model == 'Double_DQN' or self.model == 'Dueling_DDQN':
next_action = np.argmax(q_values, axis=1)
# tf.range(q_values.shape[0]构建0-batch_size的数组,next_action是q_network得出的动作,两者组合成二维数组
# 从target_q_network(next_states)输出的batch_size*action dim个数组中取数
Q2 = tf.gather_nd(target_q_network(next_states),
tf.stack([tf.range(q_values.shape[0]), tf.cast(next_action, tf.int32)], axis=1))
y_targets = rewards + (gamma * Q2 * (1 - done_vals))
q_values = tf.gather_nd(q_values, tf.stack([tf.range(q_values.shape[0]),
tf.cast(actions, tf.int32)], axis=1))
# 计算损失
loss = MSE(y_targets, q_values)
return loss
3、DDQN 和DQN实现效果对比
在同样的参数下,DDQN的收敛相对更快一点点:
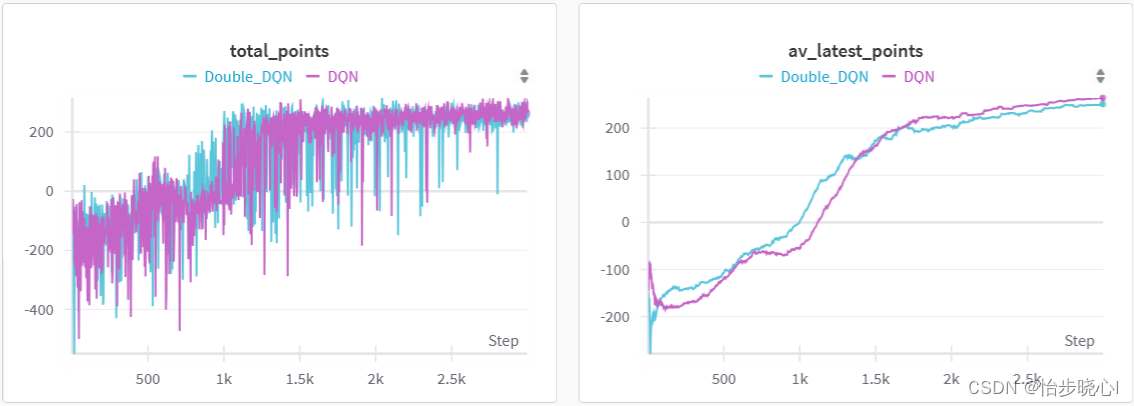
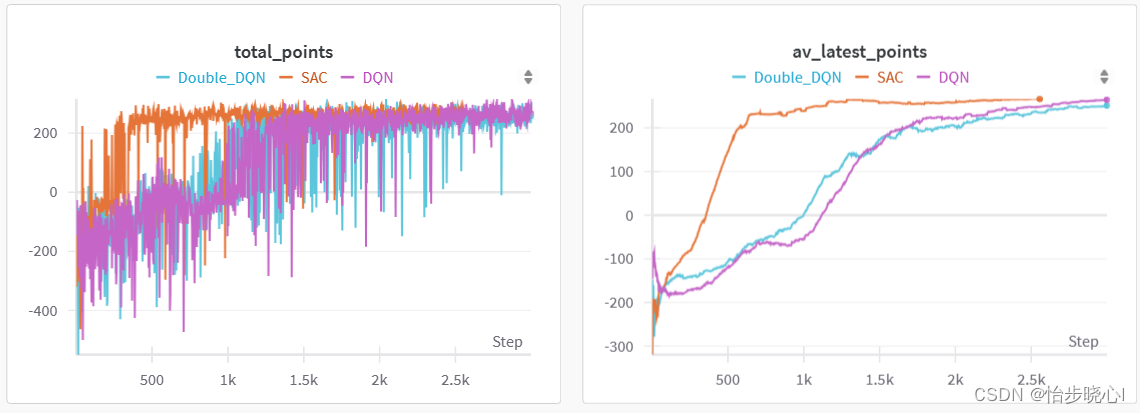
和现在非常流行的SAC算法比,差了不少嘞:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!