人工智能(AI)领域广泛使用的关键算法及其解决的问题 列出计算机中各种算法及对应解决的实际问题
2023-12-13 05:14:43
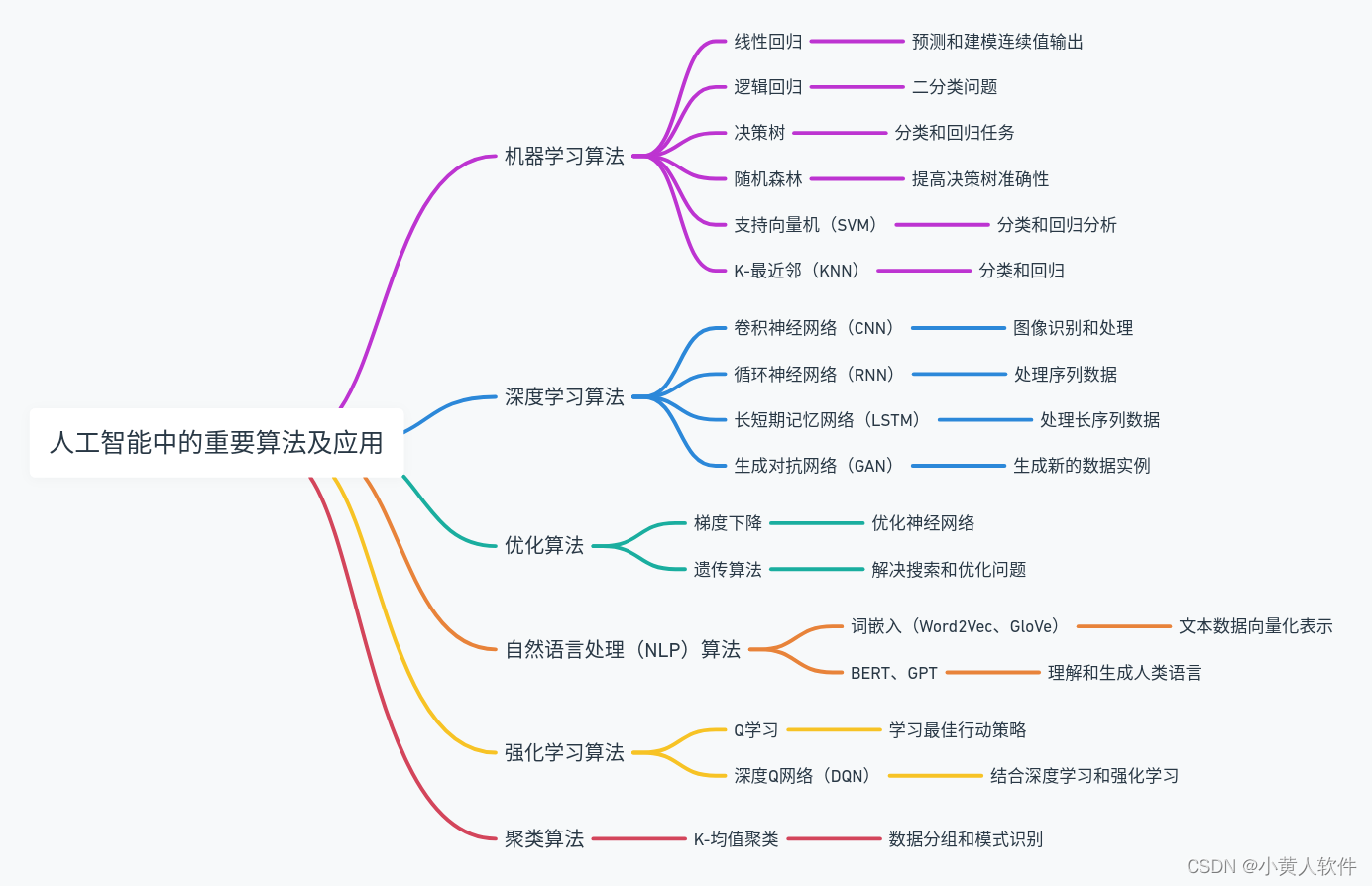
人工智能(AI)领域广泛使用的关键算法及其解决的问题:
-
机器学习算法:
- 线性回归(Linear Regression):
- 问题:用于预测或估计一个变量与另一个变量之间的关系。
- 逻辑回归(Logistic Regression):
- 问题:用于二分类问题,预测一个事件发生的概率。
- 支持向量机(Support Vector Machines, SVM):
- 问题:用于分类和回归任务,尤其适用于高维数据。
- 决策树(Decision Trees) 和 随机森林(Random Forests):
- 问题:用于分类和回归问题,易于解释且性能良好。
- 梯度提升算法(Gradient Boosting Algorithms):
- 问题:一种强大的分类和回归技术,可以用于提高模型的准确性。
- 线性回归(Linear Regression):
-
深度学习算法:
- 卷积神经网络(Convolutional Neural Networks, CNN):
- 问题:主要用于图像和视频识别、图像分类、物体检测等。
- 循环神经网络(Recurrent Neural Networks, RNN):
- 问题:处理序列数据,如时间序列分析、语言建模、文本生成。
- 长短期记忆网络(Long Short-Term Memory, LSTM):
- 问题:一种特殊的RNN,适用于处理和预测时间序列中间隔和延迟很长的重要事件。
- 生成对抗网络(Generative Adversarial Networks, GANs):
- 问题:用于生成逼真的图像、艺术作品、增强现实等。
- 卷积神经网络(Convolutional Neural Networks, CNN):
-
优化算法:
- 梯度下降(Gradient Descent):
- 问题:用于最小化损失函数,优化机器学习和深度学习模型的性能。
- 进化算法(Evolutionary Algorithms):
- 问题:用于求解优化和搜索问题,受自然选择的启发。
- 梯度下降(Gradient Descent):
-
自然语言处理算法:
- 词嵌入模型(Word Embedding Models)如Word2Vec, GloVe:
- 问题:将单词转换为向量,以便在机器学习模型中使用。
- Transformer模型(如BERT, GPT):
- 问题:用于理解和生成自然语言,改进了机器翻译、文本摘要和问答系统。
- 词嵌入模型(Word Embedding Models)如Word2Vec, GloVe:
-
无监督学习算法:
- K-均值聚类(K-Means Clustering):
- 问题:用于数据聚类,无需预先标记数据。
- 主成分分析(Principal Component Analysis, PCA):
- 问题:用于数据降维和特征提取。
- K-均值聚类(K-Means Clustering):
这些算法在人工智能的各个方面都有广泛的应用,包括图像和语音识别、自然语言处理、预测建模和数据分析等。随着技术的发展,这些算法不断被改进和优化,以解决更加复杂和多样化的问题。
列出计算机中各种算法及对应解决的实际问题
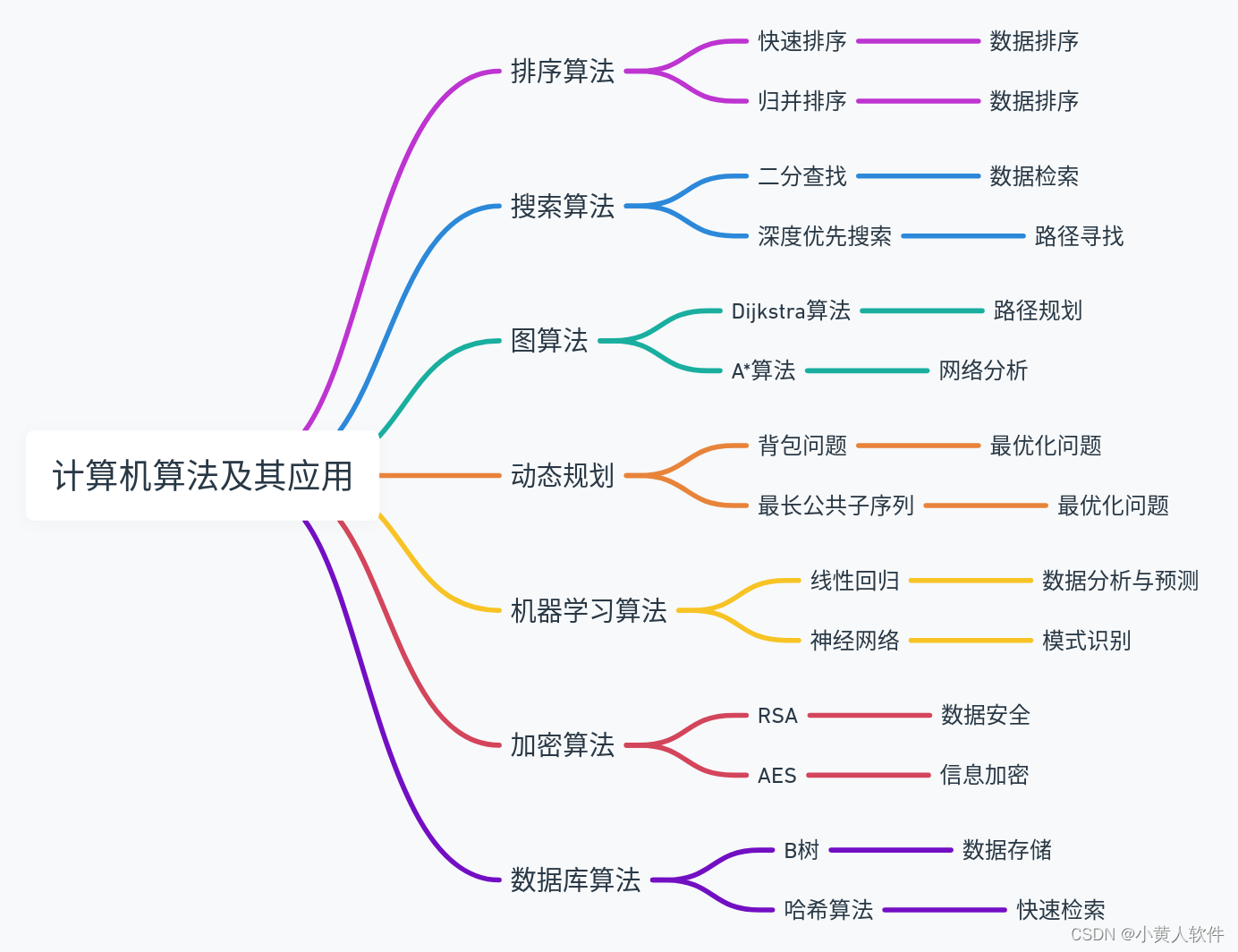
常见的算法分类:
- 按问题类型分类
- 搜索算法:用于在数据结构中查找数据或元素。常见的搜索算法包括顺序搜索、二分查找、二叉树查找等。
- 排序算法:用于将数据按特定顺序排列。常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序等。
- 最优化算法:用于求解最优解。常见的最优化算法包括贪心算法、动态规划等。
- 图算法:用于处理图形数据结构。常见的图算法包括深度优先搜索、广度优先搜索、最短路径算法、最小生成树算法等。
- 数学算法:用于解决数学问题。常见的数学算法包括求根算法、解方程算法、积分算法、微分算法等。
- 按时间复杂度分类
- 线性时间算法:时间复杂度为O(n)。
- 对数时间算法:时间复杂度为O(log n)。
- 多项式时间算法:时间复杂度为O(n^k),其中k为常数。
- 指数时间算法:时间复杂度为O(n^k),其中k为正整数。
- 按空间复杂度分类
- 常数空间算法:空间复杂度为O(1)。
- 线性空间算法:空间复杂度为O(n)。
- 对数空间算法:空间复杂度为O(log n)。
- 多项式空间算法:空间复杂度为O(n^k),其中k为常数。
以下是一些常见算法及其对应的实际问题:
- 顺序搜索:用于在有序数组中查找数据。常用于字典、电话簿等应用。
- 二分查找:用于在有序数组中查找数据。具有较高的查找效率。常用于数据库、排序算法等应用。
- 冒泡排序:用于将数据按升序排列。具有较低的排序效率。常用于简单的排序需求。
- 选择排序:用于将数据按升序排列。具有较低的排序效率。常用于简单的排序需求。
- 插入排序:用于将数据按升序排列。具有较高的排序效率。常用于简单的排序需求。
- 快速排序:用于将数据按升序排列。具有较高的排序效率。常用于复杂的排序需求。
- 归并排序:用于将数据按升序排列。具有较高的排序效率。常用于复杂的排序需求。
- 贪心算法:用于求解最优化问题。常用于网络路径选择、资源分配等应用。
- 动态规划:用于求解最优化问题。常用于最短路径问题、背包问题等应用。
- 深度优先搜索:用于遍历图形数据结构。常用于图形搜索、图形最短路径等应用。
- 广度优先搜索:用于遍历图形数据结构。常用于图形搜索、图形最短路径等应用。
- 最短路径算法:用于求解图形中两点之间的最短路径。常用于交通路线规划、物流路线规划等应用。
- 最小生成树算法:用于求解图形中的最小生成树。常用于网络路径规划、电力线路规划等应用。
-
排序算法(Sorting Algorithms):
- 问题:整理和排序数据。
- 常见算法:冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序。
-
搜索算法(Search Algorithms):
- 问题:在数据结构中查找特定元素。
- 常见算法:线性搜索、二分搜索、深度优先搜索(DFS)、广度优先搜索(BFS)。
-
图算法(Graph Algorithms):
- 问题:解决图论中的问题,如网络分析、路径查找。
- 常见算法:Dijkstra算法(最短路径)、贝尔曼-福特算法、A*算法、克鲁斯卡尔算法(最小生成树)、弗洛伊德算法。
-
动态规划(Dynamic Programming):
- 问题:解决具有重叠子问题和最优子结构的问题。
- 应用实例:斐波那契数列、背包问题、最长公共子序列。
-
分而治之(Divide and Conquer):
- 问题:将大问题分解为更小、更易管理的子问题。
- 应用实例:快速排序、归并排序、二分搜索。
-
贪心算法(Greedy Algorithms):
- 问题:在每个步骤中选择最优解,希望找到全局最优解。
- 应用实例:哈夫曼编码(数据压缩)、Prim算法(最小生成树)。
-
回溯算法(Backtracking):
- 问题:通过试错来解决问题,撤销错误步骤。
- 应用实例:N皇后问题、数独解算器、迷宫问题。
-
加密算法(Cryptography Algorithms):
- 问题:安全地传输和存储数据。
- 常见算法:RSA算法、AES算法、SHA系列。
-
机器学习算法(Machine Learning Algorithms):
- 问题:从数据中学习模式和决策规则。
- 常见算法:线性回归、决策树、支持向量机(SVM)、神经网络、随机森林。
-
排序网络(Sorting Networks):
- 问题:并行计算环境中的数据排序。
- 应用实例:Batcher奇偶归并排序网络。
每种算法都有其特定的应用场景和优缺点。选择合适的算法取决于问题的具体需求,如执行速度、内存使用、精确度和简易度等。
文章来源:https://blog.csdn.net/chenhao0568/article/details/134920391
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!