Leetcode刷题笔记——快速幂算法之万物皆可分治

递归法

算法思想

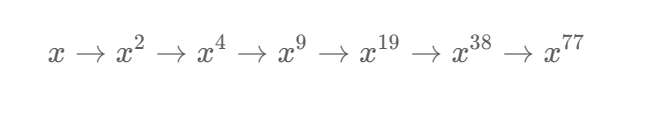
代码实现

1. 清晰易懂版

class Solution {
public:
    double myPow(double x, long int n) {
        if (n == 0) return 1;
        if (n < 0){
            return 1 / myPow(x,-n);
        }
        if (n % 2){
            return x * myPow(x,n-1);
        }
        return myPow(x*x,n/2);
    }
};

2. 拆解成两个函数版?

class Solution {
public:
    double quickMul(double x, long long N) {
        if (N == 0) {
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        return N % 2 == 0 ? y * y : y * y * x;
    }

    double myPow(double x, int n) {
        long long N = n;
        return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }
};

时空复杂度：

时间复杂度：O(log?n)

空间复杂度：O(log?n)，即为递归的层数

迭代法

算法思想

代码实现

1. 一个函数版

class Solution {
        // 迭代算法，利用二进制位
    public double myPow(double x, int n) {
        if(x == 0) return x;
        long power = n;    // 为了保证-n不溢出，先转换成long类型
        if(n < 0){         // 如果n小于0， 求1/x的-n次方
            power *= -1;
            x = 1 / x;
        }
        double weight = x;  // 权值初值为x, 即二进制位第1位的权值为x^1
        double res = 1;
        while(power != 0){
            // 如果当前二进制位为1， 让结果乘上这个二进制位上的权值, 
            // 该位权值在上一轮迭代中已经计算出来了
            if((power & 1) == 1) res *= weight;
            weight *= weight;   // 计算下一个二进制位的权值
            power >> 2;
        }
        return res;
    }
}

2. 两个函数版

class Solution {
public:
    double qpow(double a, long long b){
        double res = 1;
        while(b){
            if(b&1) res = res*a;
            b >>= 1;
            a *= a;
        }
        return res;
    }
    double myPow(double x, long long n) {
        if(n == 0) return 1;
        if(n > 0) return qpow(x,n);
        if(n < 0) return 1/qpow(x,-n);
        return 1.0;
    }
};

相关题目

??????50. Pow(x, n) - 力扣（LeetCode）

100155. 双模幂运算 - 力扣（LeetCode）