Validate Binary Search Tree

Problem

Given the?root?of a binary tree,?determine if it is a valid binary search tree (BST).

A?valid BST?is defined as follows:

• The left?

  subtree

  ?of a node contains only nodes with keys?less than?the node's key.
• The right subtree of a node contains only nodes with keys?greater than?the node's key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [2,1,3]
Output: true

Example 2:

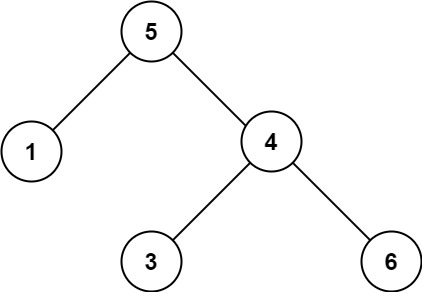
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Intuition

The task is to determine whether a given binary tree is a valid binary search tree (BST). A binary search tree is a tree in which the left subtree of a node contains only nodes with keys less than the node's key, the right subtree contains only nodes with keys greater than the node's key, and both the left and right subtrees are also binary search trees. The intuition is to perform a recursive traversal of the tree while keeping track of the valid range for each node.

Approach

Initialization:

Define a recursive helper function valid(node, left, right) that checks whether the subtree rooted at node is a valid BST within the given range [left, right].
Start the initial call with the root node and the range [-inf, +inf] representing negative and positive infinity.
Validation:

Check if the current node's value is within the valid range [left, right]. If not, return False.
Recursively call the valid function on the left subtree with the updated range [left, node.val] and on the right subtree with the updated range [node.val, right].
Return Result:

Return True if the entire tree is validated; otherwise, return False.
Invoke Helper Function:

Invoke the helper function with the root node and the initial range [-inf, +inf].

Complexity

• Time complexity:

The time complexity is O(n), where n is the number of nodes in the binary tree. Each node is visited exactly once during the recursive traversal.

• Space complexity:

The space complexity is O(h), where h is the height of the binary tree. This is because the maximum depth of the recursion stack is equal to the height of the tree. In the average case, for a balanced binary tree, the height is O(log n), making the space complexity O(log n). However, in the worst case of an unbalanced tree, the height could be O(n), resulting in a space complexity of O(n). The space complexity is dominated by the depth of the recursive call stack.

Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        
        def valid(node, left, right):
            if not node:
                return True

            if not(node.val < right and node.val > left):
                return False

            return (valid(node.left, left, node.val)) \
                    and (valid(node.right, node.val, right))
        
        return valid(root, float('-inf'), float('inf'))