2. 回归树

2023-12-27 13:35:07

目录

1. 回归树的数学表达式

1.1 公式

1.2 举例

2. 如何构建回归树

2.1 树的深度如何决定

2.1.1 第一种（确定叶子节点个数或者树的深度）

2.1.2?第二种（子节点所包含样本数）

2.1.3?第三种（给定精度）

2.2?划分的节点如何选取

2.3 叶子节点代表的值Cm如何决定

3.损失函数

3.1 公式

3.2? ?优化

3.2.1 结论

3.2.2 推导过程

1. 回归树的数学表达式

1.1 公式

f(x)=\sum_{m=1}^{M}c_mI(x\in R_m),?

  • m就是叶子结点中的序号
  • Rm是第m个叶子结点
  • Cm是第m个叶子节点的预测值
  • I指的是当后面括号里面条件满足时,为1
  • 括号中的是，x属于那个结点
  • 每个叶子节点，都会输出一个预测值
  • 预测值一般是该 叶子 所含训练样本 在该节点上的输出的均值

1.2 举例

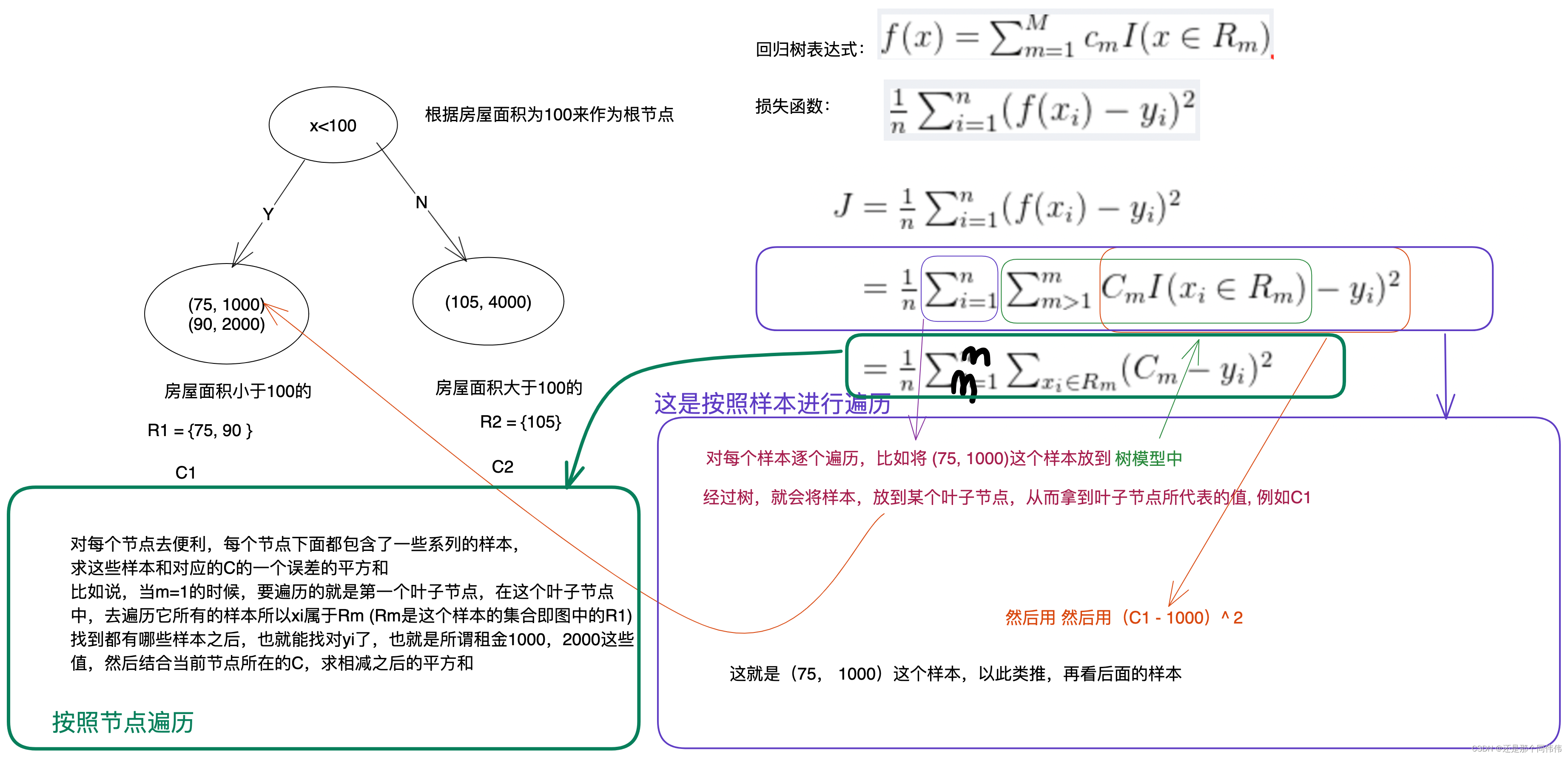
假设有数据集如下,? ?x 代表房屋面积，y代表租金

D = {(75, 1000), (90, 2000), (105, 4000)}

# 75 平的，月租1000块钱
# 90 平的 2000块钱
# 105 平的，4000块钱

????????根据图中的划分， R1（第一个叶子结点）和 R2（第二个节点）就是公式中的Rm

????????C1，C2就是公式中的Cm, 指的不是类别，是一个数，这个数和 Y的含义是一样的，即租金是多少也即是说当C1和C2这些叶子结点所代表的一些值确定的时候，当再来一个未知的样本的时候，比如说，给出房屋面积100平方，那这个房屋面积为100的样本输入进来之后，这颗树的一些路径，最后判断从那个叶子结点输出， 比如上图，102平方的房屋最后判断的是C2这个叶子结点的输出，那C2这个值就可能是5000，4500等，即就是最终预测的值。图中只是做了一次划分，而在实际中会有很多的划分。

2. 如何构建回归树

2.1 树的深度如何决定

大多数是由我们自己定义

2.1.1 第一种（确定叶子节点个数或者树的深度）

无法控制精确度

2.1.2?第二种（子节点所包含样本数）

子节点划分到多少个的时候，就不继续划分了

2.1.3?第三种（给定精度）

计算的总体的损失小于给定的精度的时候，不再划分

2.2?划分的节点如何选取

根据可以定的取值，构建出来的树，每个都计算一下对应损失，然后选损失最小的节点构建出来的数的值。

2.3 叶子节点代表的值Cm如何决定

具体可看，3.2.2的推导过程

每当叶子节点的Cm取值，为该节点所有样本yi的平均值时，得到损失最小，即最优的回归树

3.损失函数

3.1 公式

\frac{1}{n}\sum_{i=1}^{n}(f(x_i)-y_i)^2

  • n 代表样本的数量
  • i 代表第几个样本

3.2? ?优化

3.2.1 结论

C_m=\frac{\sum_{x\in R_m}y_i}{N_m}

  • N_m的含义：第m个节点中，叶子节点所包含的样本的个数

当每个叶子节点的Cm取值，为该节点所有样本yi 的平均值是，得到损失最小，即最优的回归树

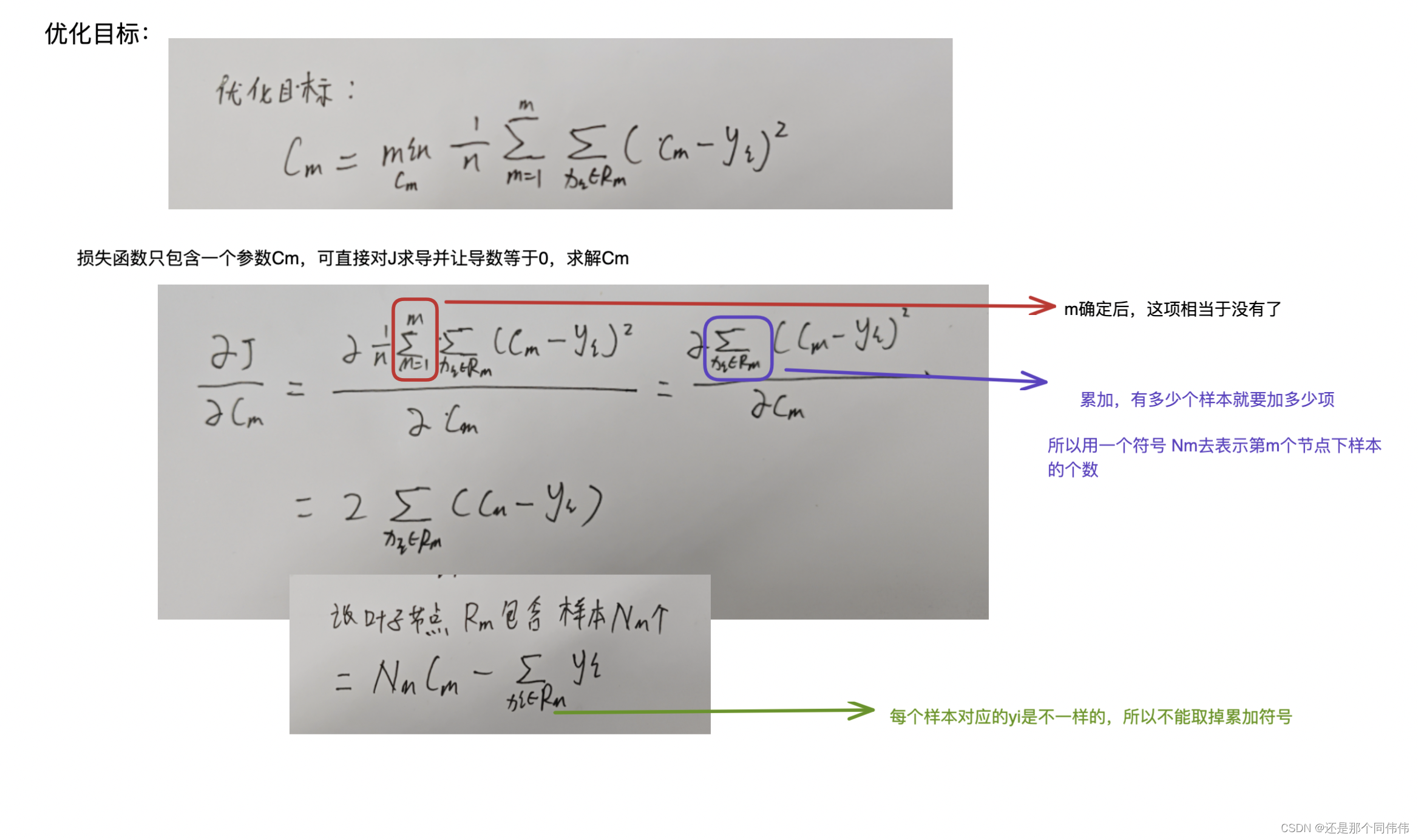
3.2.2 推导过程

即： 每当叶子节点的Cm取值，为该节点所有样本yi的平均值时，得到损失最小，即最优的回归树

未完待续

文章来源:https://blog.csdn.net/wei18791957243/article/details/135221725
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。