人工智能原理复习--搜索策略（一）

上一篇

人工智能原理复习–确定性推理

搜索概述

问题求解分为两大类：知识贫乏系统（依靠搜索技术解决）、知识丰富系统（依靠推理技术）
两大类搜索技术：

1. 一般图搜索、启发式搜索
2. 基于问题规约的与或图搜索

求解问题包括：1. 目标表示 2.搜索 3.执行
初始状态集合和操作符集合定义了问题的搜索空间

搜索策略评价标准：

1. 完备性
2. 最优性
3. 时间复杂性
4. 空间复杂性

一般图搜索

状态空间搜索是一般图搜索的代表形式，用状态空间搜索来求解问题的系统均定义一个状态空间，并通过适当的搜索算法在态空间中搜索解答路径。

状态空间表示法：定义状态的描述形式，将一切状态表示出来，再定义一组操作算子，通过他们将问题由一种状态转变为另一个状态。问题求解过程就是不断通过操作作用于状态的过程，得到操作状态到目标状态所用的操作序列的过程。

而使用操作最少或较少的解称为最优解，采用不同的搜索策略得到的结果顺序也可能不同。



状态空间可表示成二元组(S, O)：
S:表示所有可能到达的合法状态构成的集合
O:表示操作算子的集合
状态就用一个矢量来表示某一时刻问题现状的快照

状态空间图：1. 结点：状态 2. 有向弧：状态的变迁 3.弧上的标签：导致状态变迁的操作算子
问题的状态空间是一个表示该问题的所有可能状态及其变迁的有向图

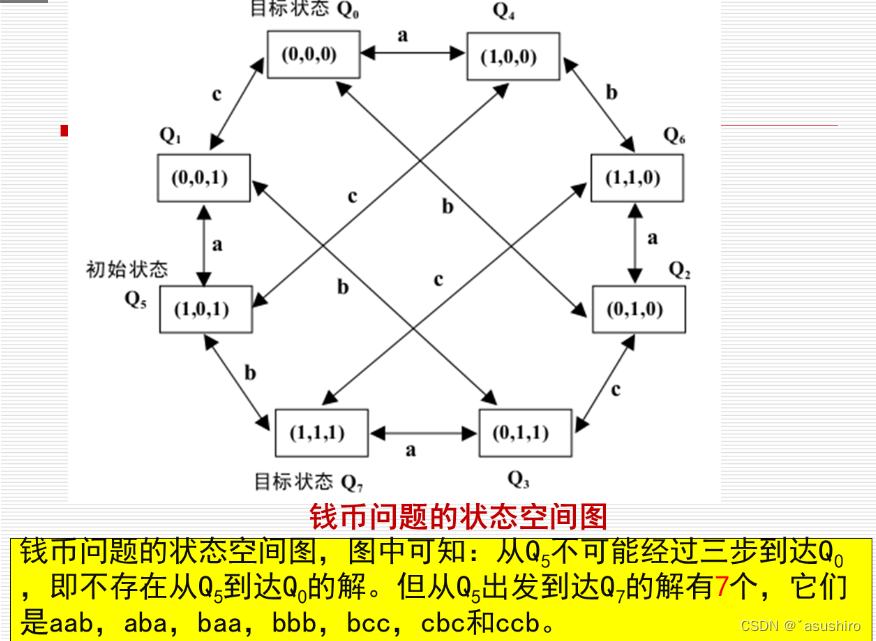
状态空间表示例子

1. 状态：(1, 0, 1) 表示状态位（正，反，正）
2. 操作算子：
   a:表示翻转第一个钱币
   b:表示翻转第二个钱币
   c:表示翻转第三个钱币

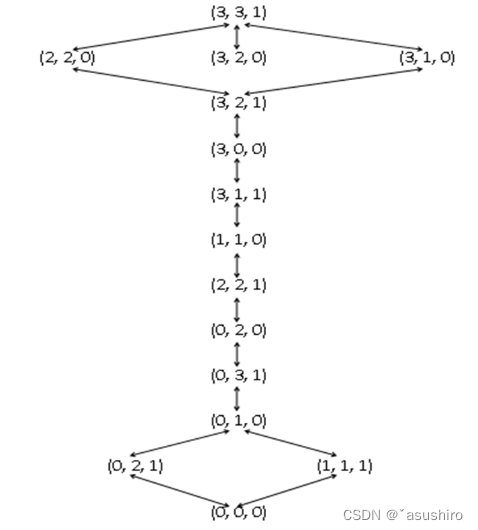
传教士与野人问题
描述：N个传教士带领N个野人划船过河；
需要满足三个约束条件：

1. 船上人数不得超过载重限量，设为K个人
2. 任意时刻（包括两岸、船上）野人数量不得超过传教士
3. 允许在河的某一岸或者在船上只有野人而没有传教士

求解当N = 3，K = 2时的状态空间有向图
解：
状态表示：
（m, c, b）表示(传教士在左岸的实际数量，野人在左岸实际数量，船是否停在左岸（0/1）)
共有 4 x 4 x 2 = 32中状态
其中合法状态：

1. 左岸传教士和右岸传教士人数大于野人
   m = 1, c = 1; m = 2, c = 2;
2. 左岸只有野人没有传教士
   m = 0, c = 0, 1, 2, 3
3. 左岸只有传教士没有野人
   m = 3, c = 0, 1, 2, 3

不可能达到的合法状态：

• (0, 0, 1）人过去了船飘了回去
• (0, 3, 0) 传教士过去不带野人不符合目的
• (3, 0, 1) 野人过去但是船回来了
• (3, 3, 0) 只有船过去了

操作算子：
L(x, y)表示从左岸向右岸划船,x表示传教士人数，y表示野人数量
R(x, y)表示从右岸向左岸划船,x表示传教士人数，y表示野人数量

x, y取值为(1, 0) , (2, 0), (1, 1), (0, 1), (0, 2)
可以看出野人自己也会划船

而整个状态空间搜索可以用五元组表示：
SE=(S,O,E,I,G)
E–搜索引擎（搜索策略/算法）
I–问题的初始状态
G–问题的目标状态

基本思想：通过搜索引擎E寻找一个操作算子的调用序列，使问题从初始状态I变迁到目标状态G之一。
解答路径就是从初始状态到目标状态的操作算子的调用序列。

搜索树：
一般图的搜索过程是或图，操作算子之间时一种“或”的关系

搜索术语：

1. 节点深度：根节点指示初始状态，不同情况对应的操作顺序长度
2. 节点扩展：应用操作算子将上一状态转变到下一状态而拓展出节点
3. 路径：要求路径是无环的
4. 路径代价：

符号说明：
s – 初始状态节点
G – 搜索图
OPEN – 存放待扩展节点的表
CLOSE – 存放已被扩展的结点的表
MOVE-FIRST(OPEN) – 取OPEN表首的节点作为当前要被扩展的节点n同时将结点n移至CLOSE表

分为两个阶段：

1. 初始化
   • 建立只包含初始结点s的搜索图G:={s}
   • OPEN:={s}
   • CLOSE:={}
2. 搜索循环
   • MOVE-FIRST(OPEN)-取出OPEN表首的结点n作为扩展节点，同时将其移到close表
   • 拓展n的子节点，插入图G和OPEN表
   • 适当标记和修改指针
   • 排序OPEN表

扩展的节点分为3类：

1. 全新节点(直接加入到OPEN表中)
2. 已出现在OPEN表中的节点（在OPEN表排序，找最短搜索顺序）
3. 已出现在CLOSE表中的节点（当前确定的路径）

盲目搜索

提高搜索效率的关键是优化OPEN表中节点的排序方式

BFS
扩展当前节点后生成的子节点总是置于OPEN表的后端，及OPEN表作为队列，先进先出，是搜索优先向横向方向发展。

性质：

1. 当问题有解时，一定能找到解
2. 当问题为单位代价时，有解时，一定能找到最优解
3. 效率较低，具有通用性，属于图搜索方法

优缺点：

1. 找到目标节点的路径最短
2. 时间和空间复杂度都比较高，无用节点较多

DFS
扩展当前节点后生成的子节点总是置于OPEN表的前端，即OPEN表作为栈，后进后出，使搜索优先向纵深方向发展。

由于人工智能中一条路径的深度不可测，所以这样做不一定找得到最佳解，甚至可能找不到解，所以为了保证能找到解所以应加上深度界限(有界DFS)，或者采取不断加大深度界限的办法，反复搜索(迭代加深DFS)。

DFS的性质：

• 不能保证找到最优解
• 当深度限制不合理时，可能找不到解
• 最坏情况下相当于穷举，是一个通用的与问题无关的方法

优缺点：
优点：比BFS使用较少的空间
缺点：既不是完备的，也不是最优的

BFS与DFS的比较

	DFS	BFS
适用场合	当问题有多个解且只需要找到其中一个时，往往对深度进行限制	确保搜索到的是最短路径
共同优缺点	优点：不需要设计排序方法，简单易行,适用于复杂度不高的问题	缺点：节点排序的盲目性，白白搜索了大量无关的状态节点

有界DFS
按深度优先算法进行，但是要给深度一个限制

深度dm很重要，当dm过小时可能找不到解是不完备的，当dm过大时，搜索过程会产生过多的无用节点，即浪费了计算机资源，又降低了搜索效率

主要问题就是深度限制值dm的选取

迭代加深搜索
先任意给定一个较小的数作dm，然后按有界深度算法搜索，若在此深度限制内找到了解，则算法结束，否则增大深度限制dm，继续搜索。

相对于整个树的结点来说，距离根节点的节点就是很少的，对这些节点反复扩展对于整个树来说是很小的，所以相对看了负担实际很小。

四种方法的比较

• 四种方法都可以用于生成和测试后面改进的算法的性能
• 宽度优先搜索需要指数数量的空间，深度优先搜索的空间复杂度和最大搜索深度呈线性关系
• 迭代加深搜索对一颗深度受控的树采用深度优先的搜索，它结合了宽度优先和深度优先的优点，和宽度优先搜索一样，它是最优的，也是完备的。但对空间要求和深度优先搜索一样是适中的。

标准	宽度优先	深度优先	有界深度	迭代加深
时间	$b^d$	$b^m$	$b^{dm}$	$b^d$
空间	$b^d$	$b?m$	$b?dm$	$bd$
最优	是	否	否	是
完备	是	否	如果$dm>d$	是

b是分支系数，d是解答深度，m是搜索树的最大深度，dm是深度限制

下一篇

人工智能原理复习–搜索策略（二）