python统计分析——直方图（sns.histplot）

使用seanborn.histplot()函数绘制直方图

from matplotlib.pyplot as plt
import seaborn as sns

data_set=np.array([2,3,3,4,4,4,4,5,5,6])
plt.hist(fish_data)

（1）data=None,  表示数据源。
（2）x=None, 表示直方图的分布垂直与x轴。单位序列型数据时，默认垂直于x轴。
（3）y=None, 表示直方图的分布垂直于y轴。

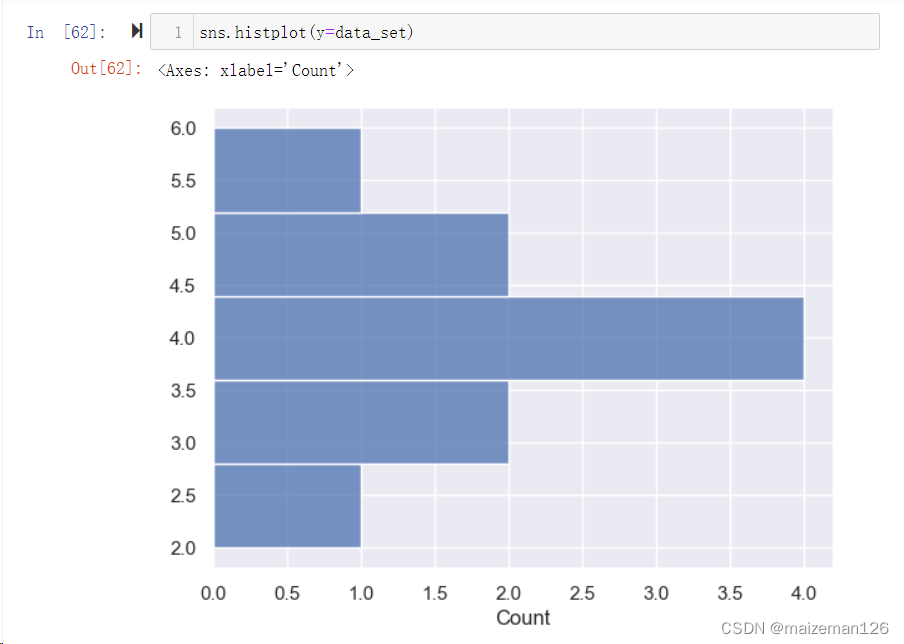
（4）hue=None, 用于区分数据系列。

df=pd.DataFrame(data={
    'type':['A','A','A','A','A','A','A','A','A','A','B','B','B','B','B','B','B','B','B','B'],
    'value':[2,3,3,4,4,4,4,5,5,6,5,6,6,7,7,7,7,8,8,9]
})
sns.histplot(data=df,x='value',hue='type')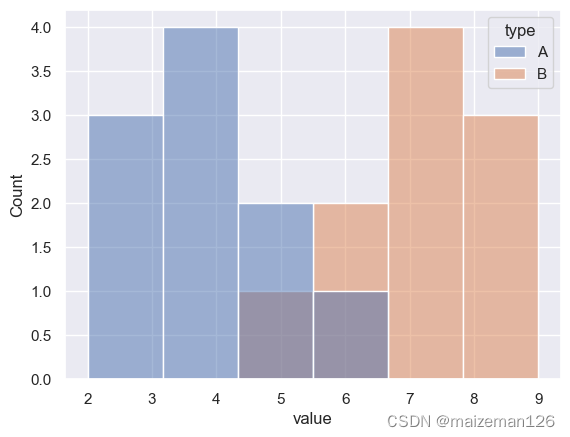

（5）weights=None, 表示对数据设置权重，要求权重序列的长度与作图的数据点的长度一致。

df=pd.DataFrame(data={
    'type':['A','A','A','A','A','A','A','A','A','A','B','B','B','B','B','B','B','B','B','B'],
    'value':[2,3,3,4,4,4,4,5,5,6,5,6,6,7,7,7,7,8,8,9],
    'weight':[2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1]
})
sns.histplot(data=df,x='value',weights='weight')

图中A的权重是B权重的2倍。

（6）stat='count', 默认为count，表示频数统计。还有frequency、probability、percent、density。frequency表示频数除以极差（全距）；probability表示用小数点表示的频率；percent表示用百分数表示的频率；density表示概率密度，为frequency之和归一处理后的数据。

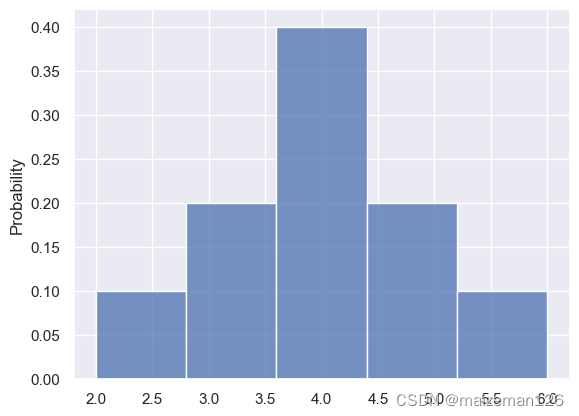
（7）bins='auto', 表示数据桶的数目，即直方图呈现出的数据组数。当bins为一个整数时，表示需要分组的数目；当bins为一个数据序列时，表示用于分组的临界值。举例说明：当bins=[1,2,3,4]时，用于分组的区间为：[1,2)、[2,3)、[3,4]；当bins为文本时，表示作图时的分组策略，可用选项具体有：'auto', 'fd', 'doane','scott', 'stone', 'rice', 'sturges', 'sqrt'。下图为“rice”分组策略为例，其余的可以自行尝试。

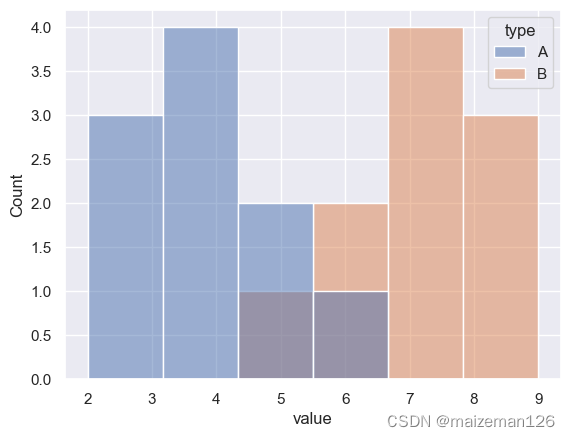
（8）binwidth=None, 用于设置数据桶的组距，下图设置组距为0.8，即binwidth=0.8。

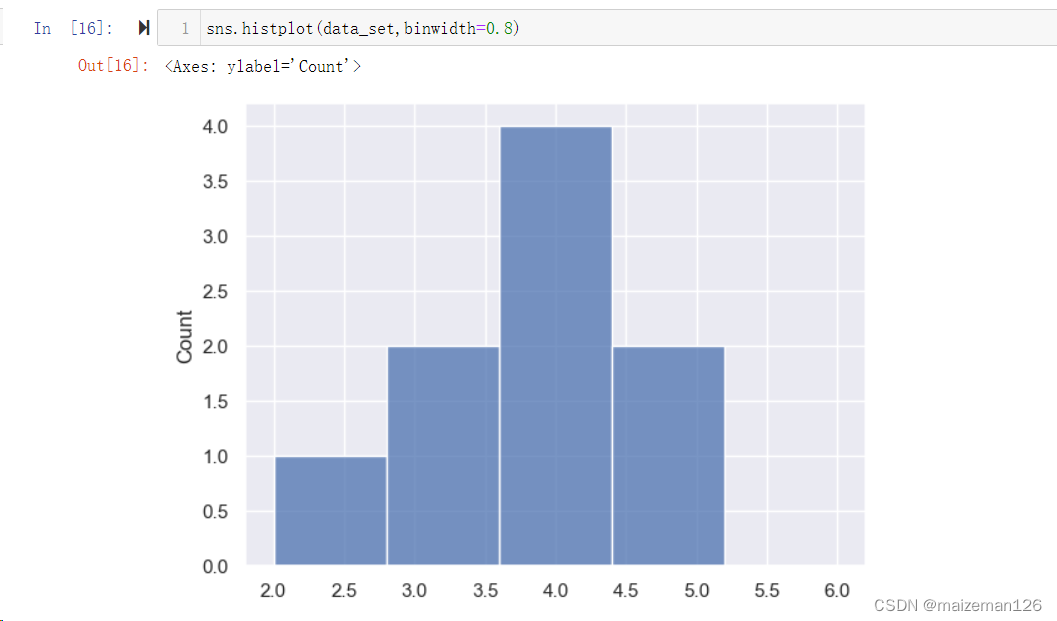
（9）binrange=None, 用于设置绘制直方图的数据源的上下限，低于下限或高于上限的数据将不参与绘制。下图设置的组距是3-5。

（10）discrete=None, 用于告诉程序数据是否是离散型数据，如果设置为True，则按照离散型数据绘制直方图。下图中注意看横坐标的变化。

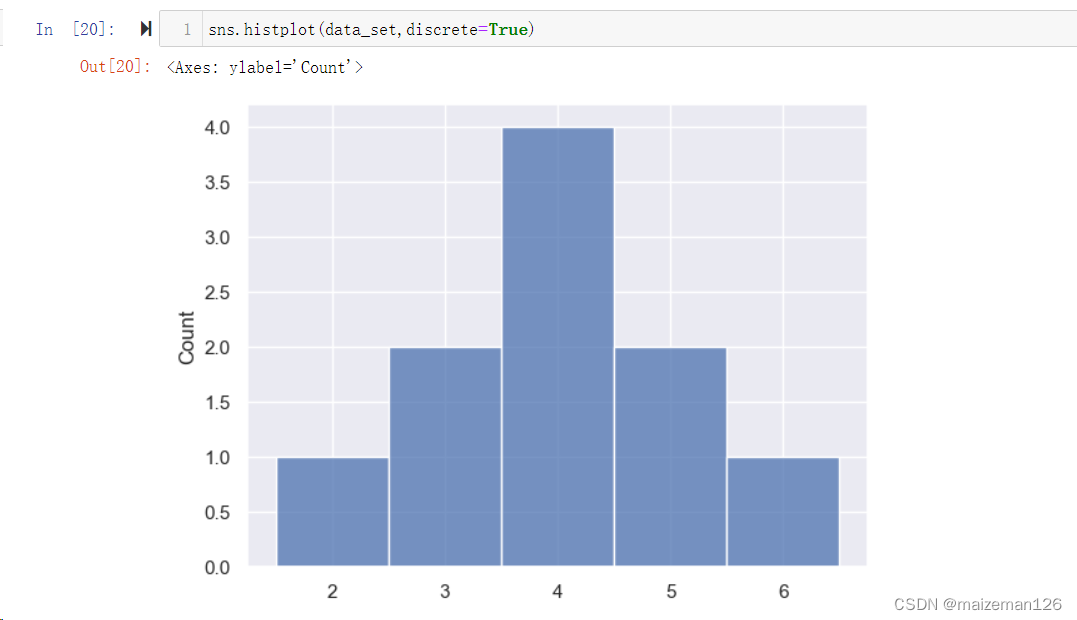
（11）cumulative=False, 如果设置为True表示对数据进行累加。

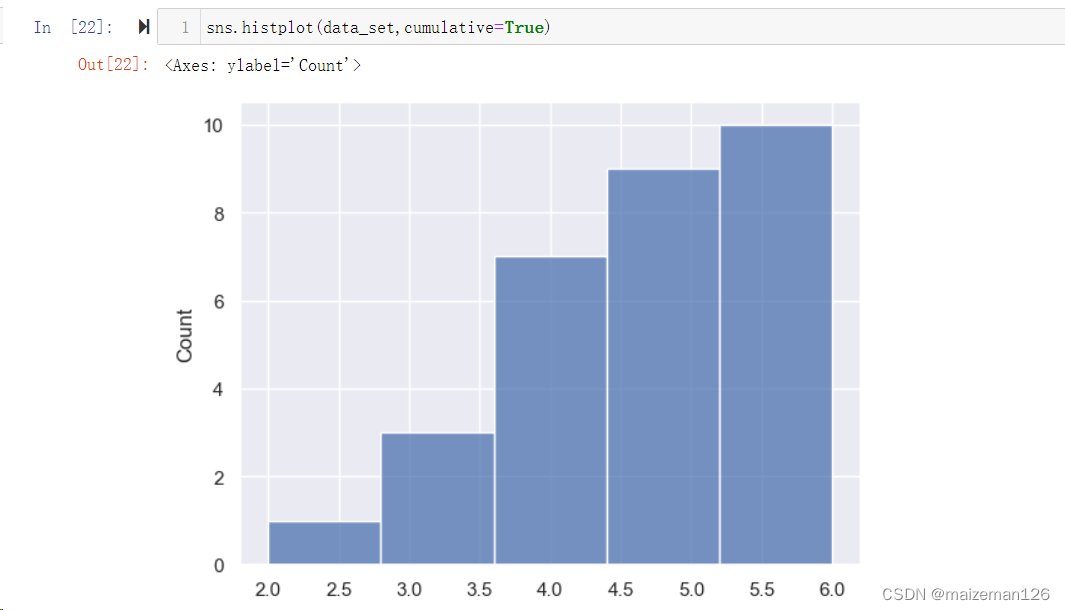
（12）common_bins=True, 当存在两组或多组数据时，用于明确分组依据是否按照统一标准进行。默认为统一标准。当设置为False时，即各自按各自分组依据进行，作图如下：

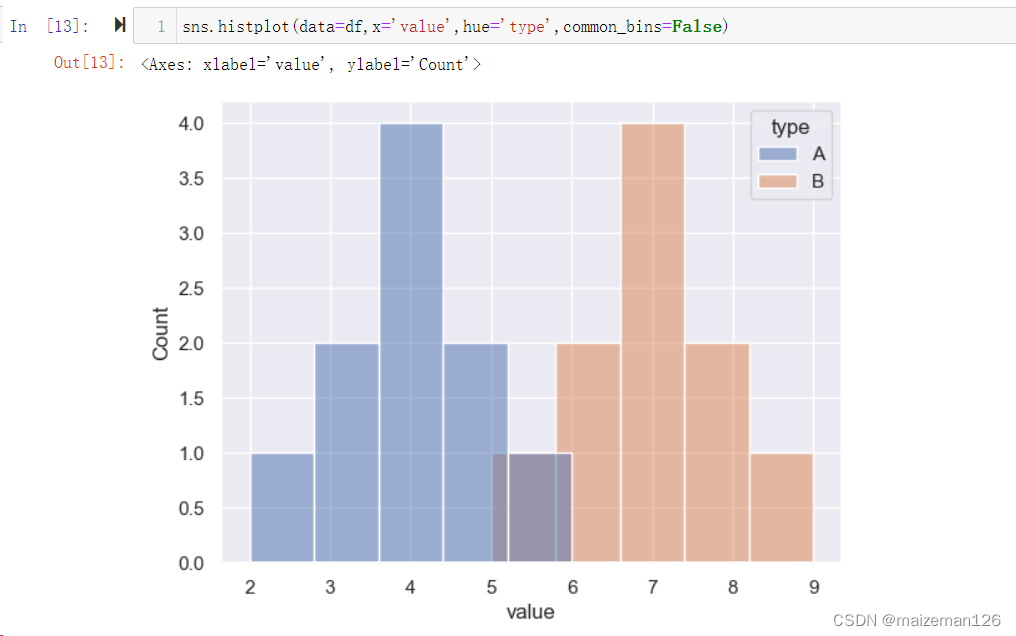
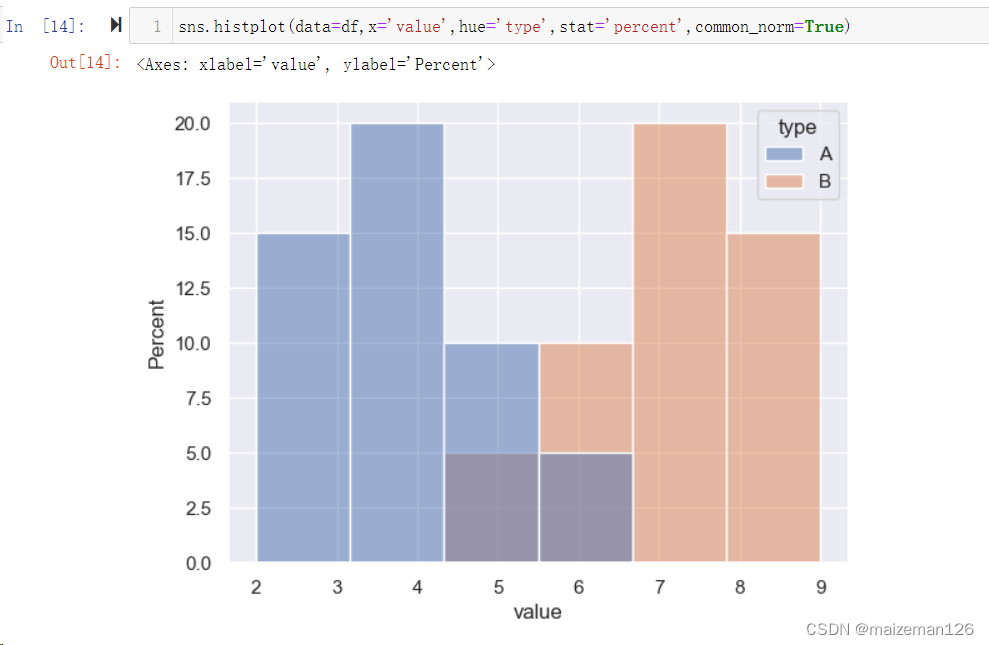
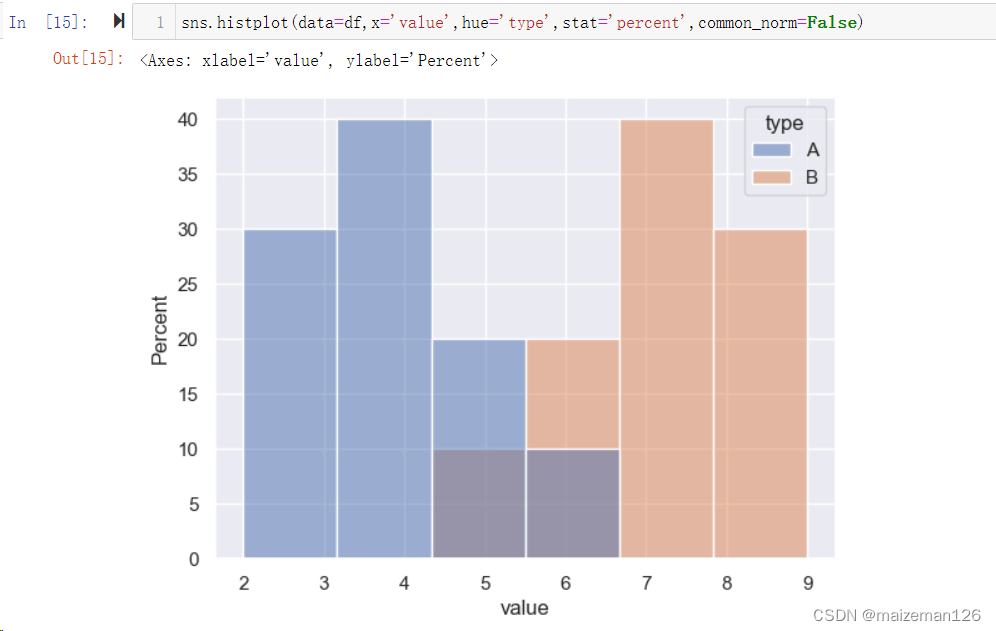
（13）common_norm=True, 当分组数据作图，stat设置为‘percent’或‘density’时，如果设置为True，表示按整体进行汇总转换，当设置为False时，表示按各组自己的数据汇总转换。下图分别为True和False的设置，注意看纵坐标轴的变换。

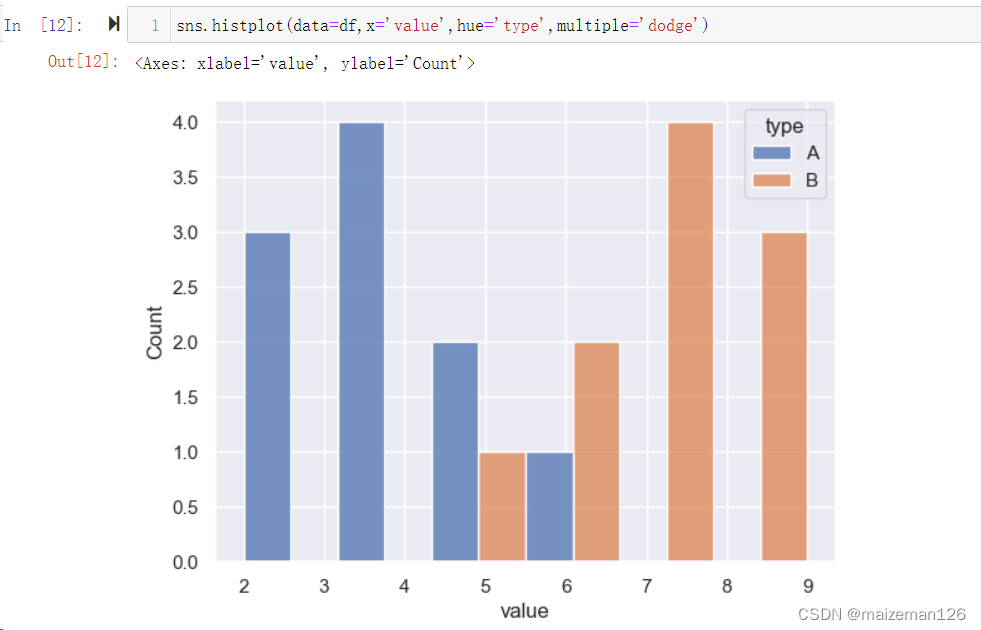
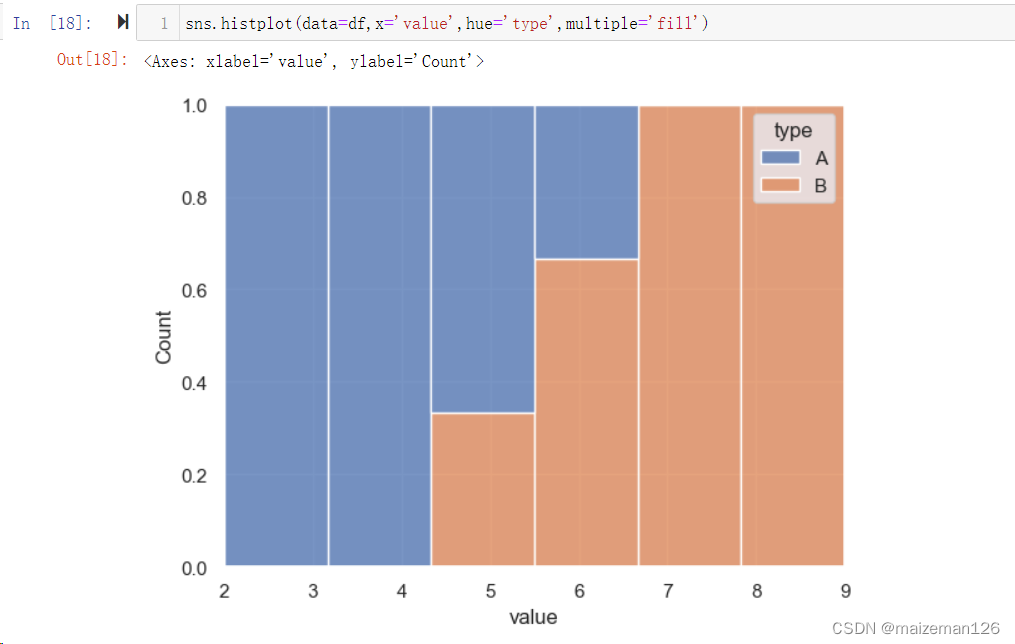
（14）multiple='layer', 用于设置分组数据的展现形式。有layer、dodge、stack、fill四种设置。

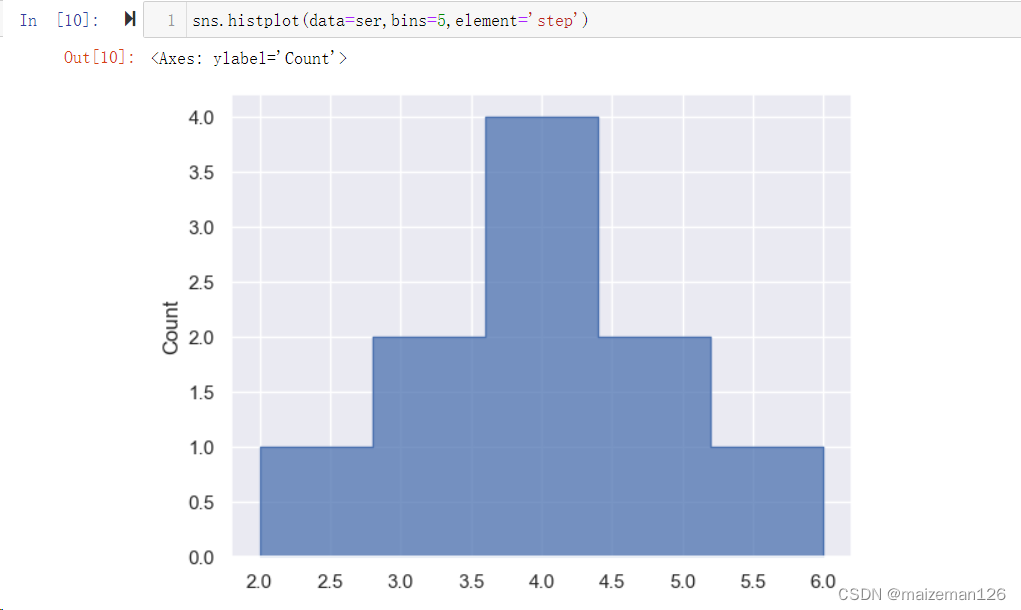
（15）element='bars', 用于设置直方图的表现形式。有bars、step和poly三种设置。

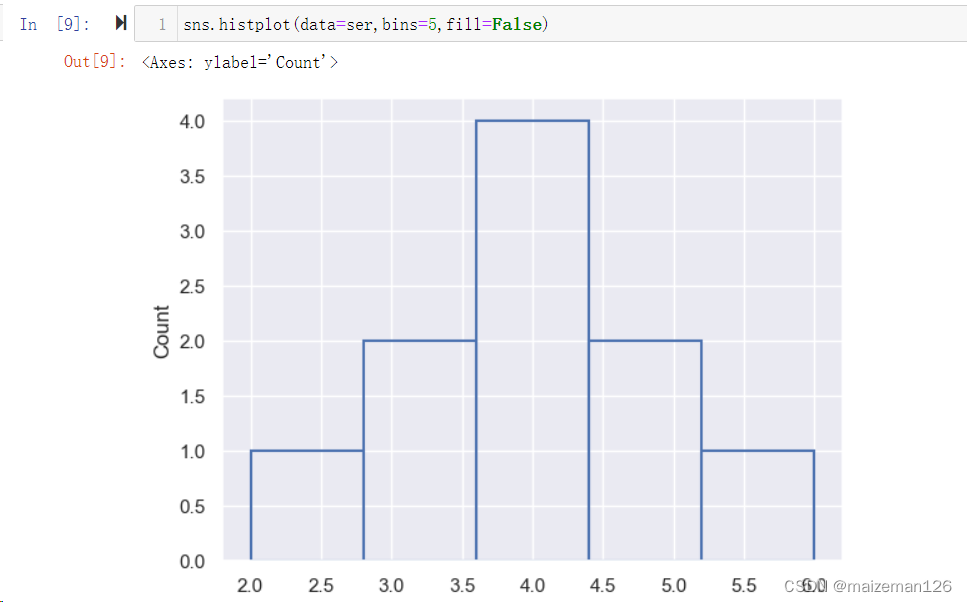
（16）fill=True, 用于设置条形图是否有填充，默认为True，下图为设置为False的展示。

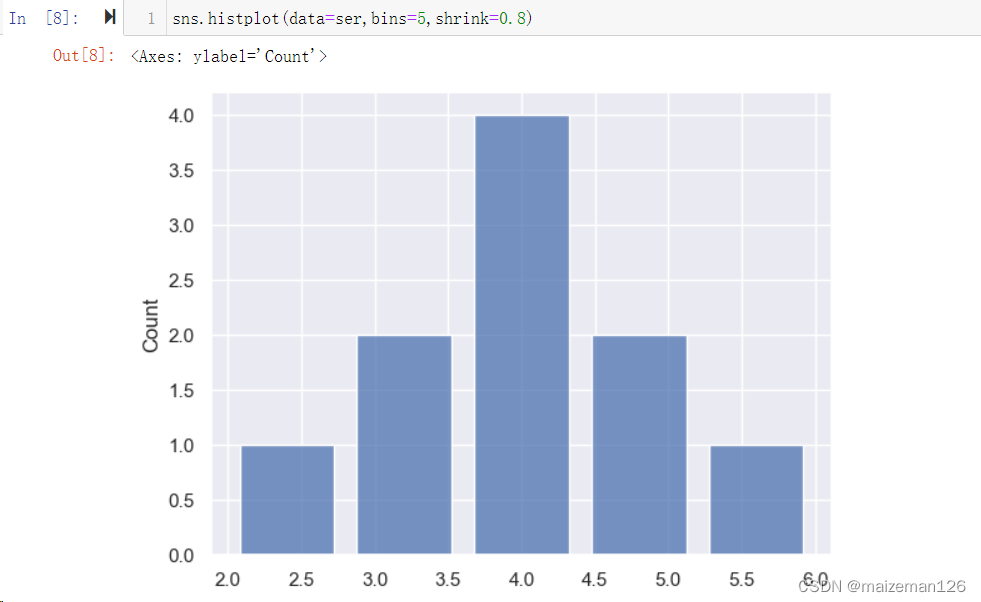
（17）shrink=1, 用于设置条形图的宽度相对于组距的宽度，默认为1，即二者相等。下图为设置为0.8的效果。

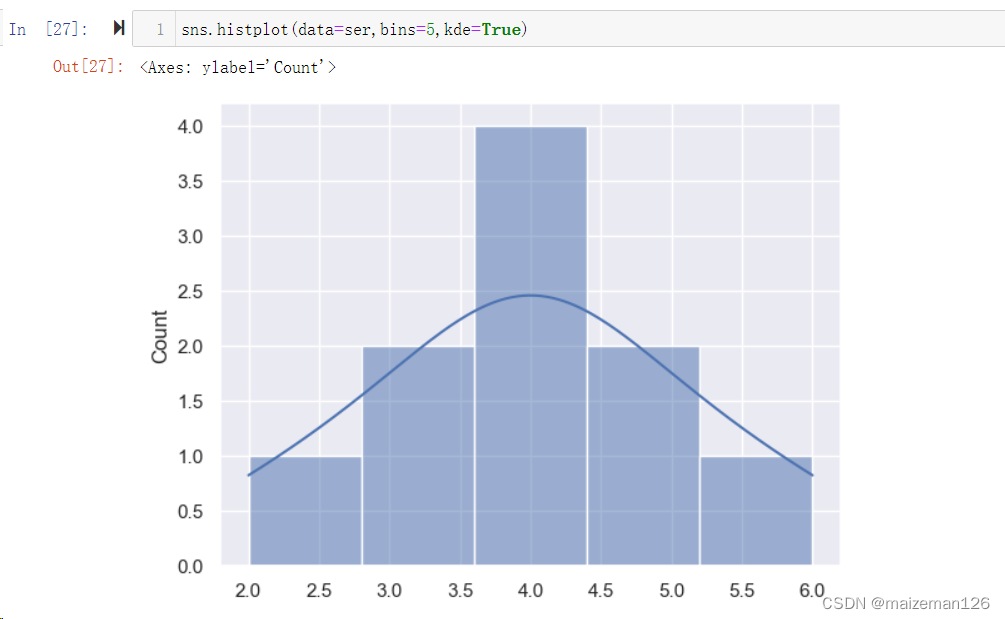
（18）kde=False, 用于设置是否显示核密度曲线（概率密度函数是一个已知概率分布的函数，用于描述随机变量的概率分布。而核密度函数是一种基于数据样本的估计方法，用于估计数据的概率密度，并生成一个平滑的密度曲线。因此，概率密度函数是一种理论上的概念，而核密度函数是一种实际上用于估计概率密度的方法。）

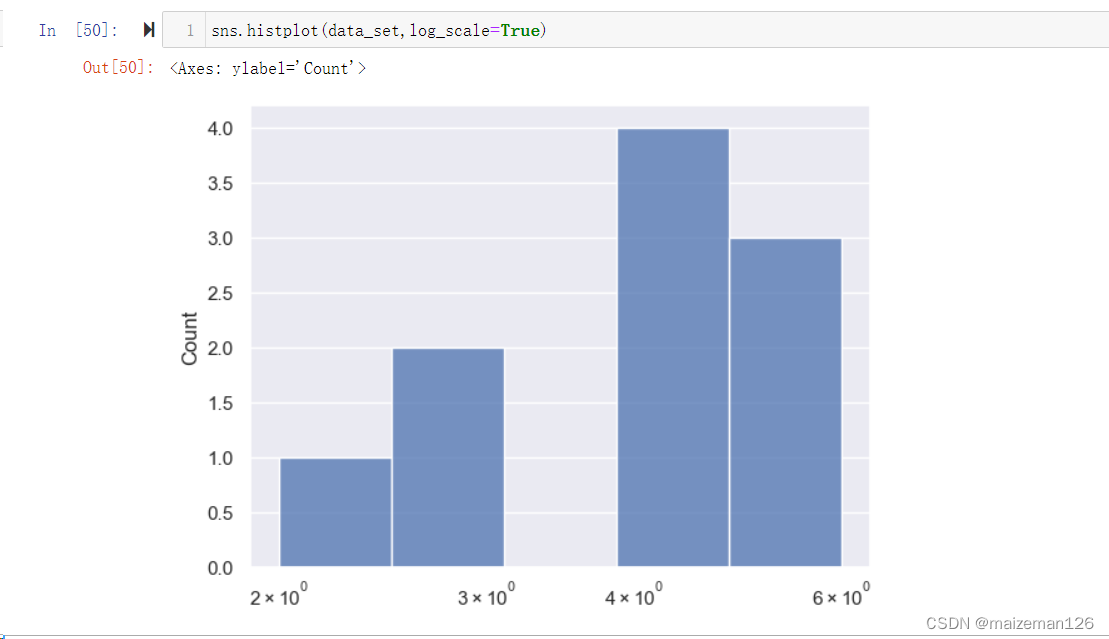
（19）log_scale=None, 由于设置是否对数据进行对数转换。