综合评价---DEA数据包络分析
数据包络分析(Data Envelopment Analysis，DEA)，1978年由 Charnes、Cooper和Rhodes创建的一种绩效评价技术(performance technique) 。采用多投入、多产出数据对多个决策单元(Decision Making Unit) 的相对效率进行评价因DEA的诸多优势，被广泛应用于效率和生产率评价。其中，包络的意思是对不同决策单元进行效率评价时的参照系(前沿面【构造一个最优的或最好的标准】)，把每一个个体与包络线之间进行一个比较，然后进行分析。包络在微观经济学中通常讲长期的平均成本曲线是短期平均成本曲线的包络线（长期成本比短期成本低）。
一、DEA相关概念
1、DMU（决策单元）
决策单元是指可以将一定的输入转化为相应的产出的运营实体，并且每一个决策单元都有m种输入和s种输出。
决策单元用效率（用）评估其好坏，产出越大越好，投入越节省越好。
特点：同类型、同输入指标、同输出指标。如：浙江、江苏这种都是省级别，只有同类型的决策单元才可以相互比较，否则无法比较
数量：DMU变量数量≥指标数的3倍。DMU数量过少容易导致很多DMU都在前沿面上，模型最终效果不精准
2、角度（导向）选择
投入导向：在产出不变的情况下，投入减少多少，效率达到有效。
产出导向：在投入不变的情况下，增加产出多少，效率达到有效。
非导向：同时从产出、投入角度处理，使效率达到有效。
投入导向问题时，产出可以有负数和0，投入不能有负数和0
产出导向问题时，投入不可以有负数和0，产出可以有负数和0
非导向问题时，投入和导出都不能有负数和0
3、规模报酬选择：CRS与VRS
CRS和VRS是两个常用的模型。它们都是用于评估 DMU的技术效率，即通过比较每个 DMU 的输入和输出，确定每个 DMU 是否有效率。CRS 模型假设生产者的规模效率是恒定的，即输入量和输出量呈线性比例关系（投入增加一个倍数，产出增加相同的倍数）。VRS 模型相对于 CRS 模型而言更加通用，因为它假设生产者的规模效率是可变的，即输入量和输出量呈非线性比例关系。即CRS(规模报酬可变：折线)、VRS(规模报酬不可变：虚线)
4、效率前言（前沿面）
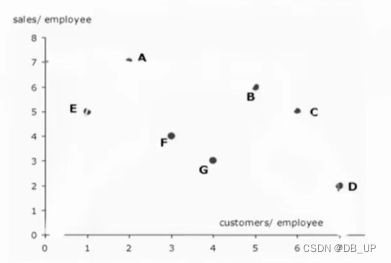
决策单元A和D/F，E和F谁好？如何衡量DMU的好坏？-------前沿面
1）单投入单投出
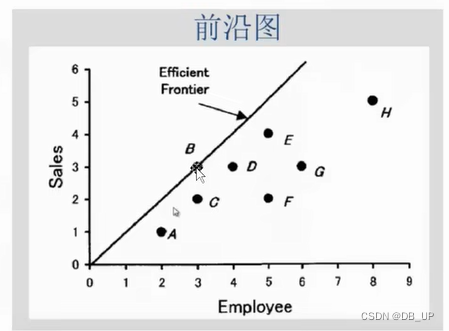
2）两投入单产出
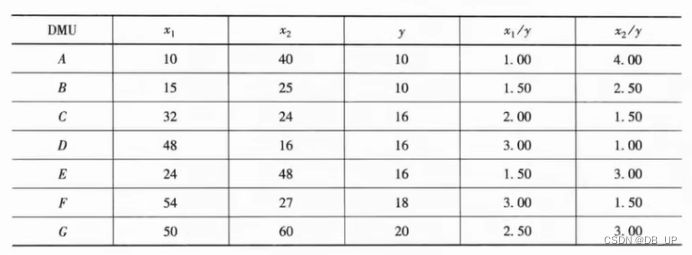
前沿面构造如下：
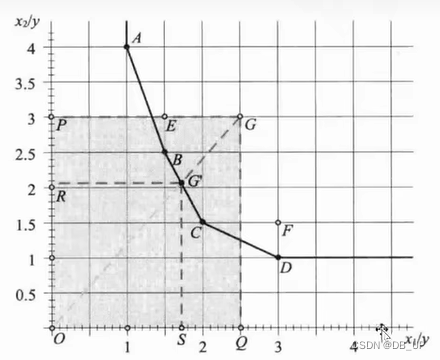
3）单投入两产出
前沿面构造如下：
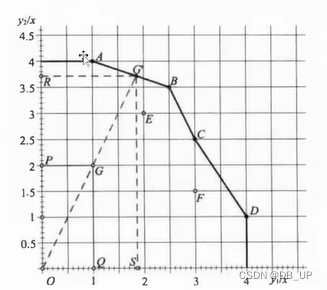
通过改进距离来评价效率
前沿面分：当期、全局
当期：所有的个体当期的投入产出数据构造一个前沿面来评价这一年的效率
全局：所有时期的投入产出数据构造一个前沿面来评价这一年的效率
5、模型选择
模型选择：径向、非径向
径向问题：等比例投影（固定比例缩小/扩张）
非径向问题：不等比例投影（不固定比例缩小/扩张）
混合问题：既考虑径向又考虑非径向
6、标准效率模型、超效率模型
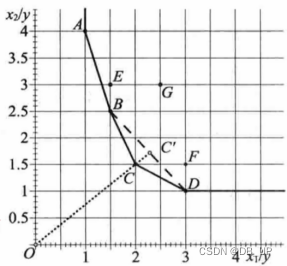
标准效率模型，超效率模型（标准效率模型效率值最大就是1，效率值都为1的进行排序用到超效率模型）
A、B、C、D都是在前沿面上，效率值都为1，谁的效率更高？
假设计算C点的效率，前沿面为ABD，C的效率等于>1
计算B/D点的效率，前沿面为ACD/ABC，B/D的效率等于1
二、CCR模型
1978年，Charnes、Cooper和Rhodes提出了DEA理论方法，以三人姓氏的首字母命名他们创立的第一个DEA模型，即CCR模型。
CCR模型：当期、标准效率、投入导向
CCR模型：全局、标准效率、投入导向
CCR模型：当期、标准效率、产出导向
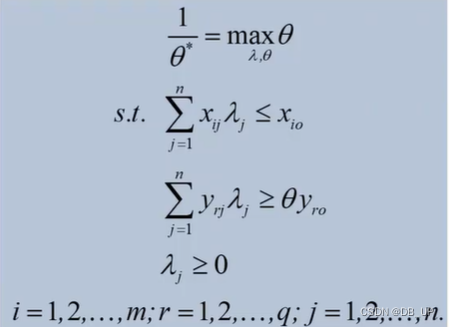
CCR模型：全局、标准效率、产出导向
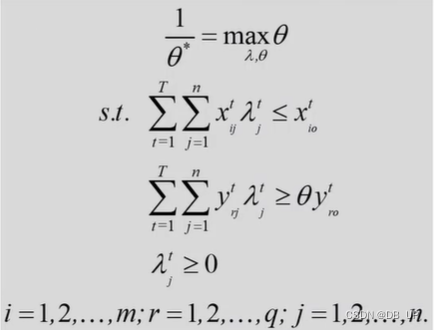
CCR模型：当期、超效率、投入导向
超效率与标准效率区别就是超效率剔除了自己本身数据
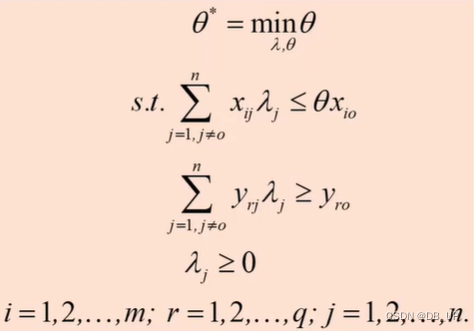
三、BCC模型
1984年，Banker、Charnes和Cooper基于规模报酬可变的假设拓展了DEA方法，即BCC模型。
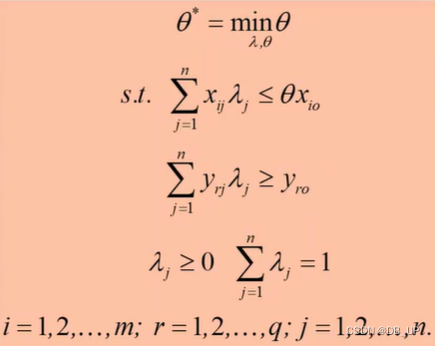
四、SBM模型
Tone 于2001年提出了SBM模型(SlackBased Measure) ，其优点是解决了径向模型对无效率的测量没有包含松弛变量的问题。
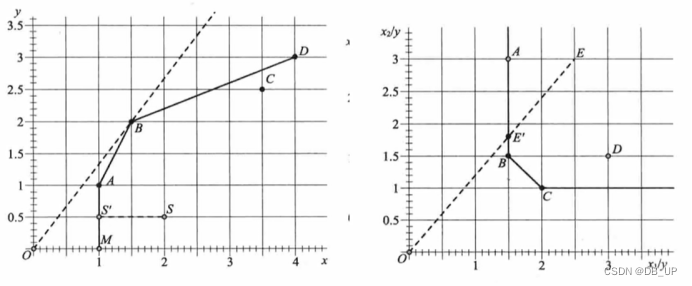
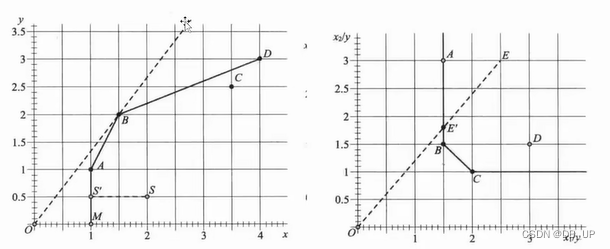
x：投入 y：产出
产出松弛：S----弱有效，因为投入不变(X)的情况下，产出可以增加到更大，产出冗余(----A)
投入松弛：E----弱有效，因为投入不变(X1)的情况下，投入x2可以继续减少，投入冗余(----B)
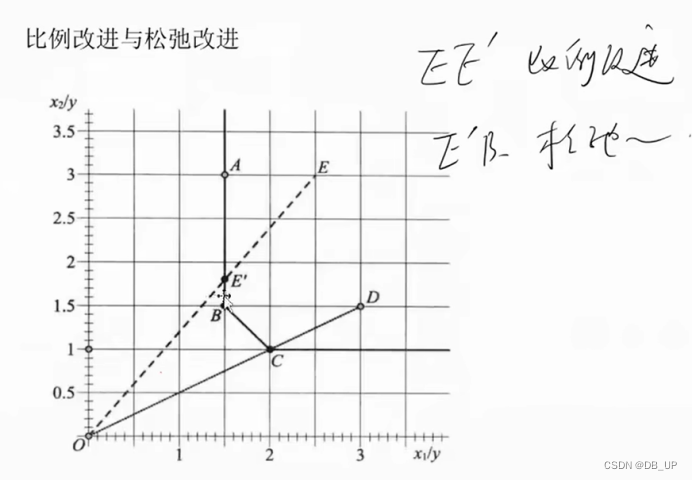
SBM模型：当期、标准效率、投入导向
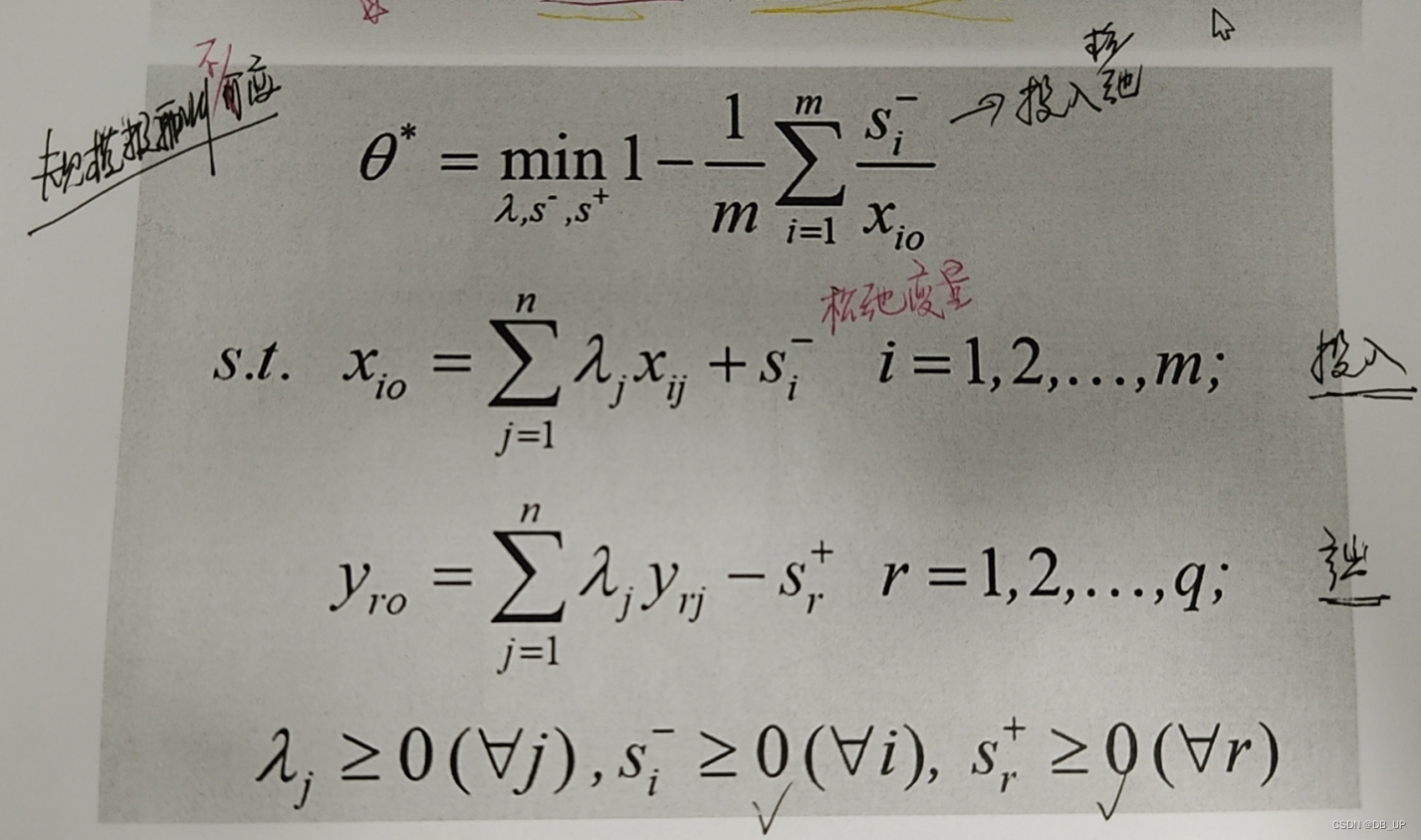SBM模型：当期、标准效率、产出导向
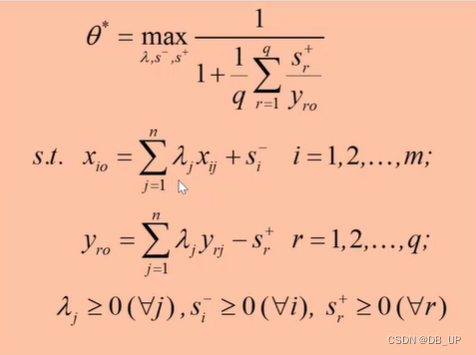
SBM模型：当期、标准效率、非导向
五、传统DEA-python实现
import gurobipy #规划求解包
import pandas as pd
#DMUs_Name：决策单元，X：投入数据；Y：产出数据
class DEA(object):
def __init__(self, DMUs_Name, X, Y, AP=False):
self.m1, self.m1_name, self.m2, self.m2_name, self.AP = X.shape[1], X.columns.tolist(), Y.shape[1], Y.columns.tolist(), AP # shape 行数 columns.tolist列名
self.DMUs, self.X, self.Y = gurobipy.multidict({DMU: [X.loc[DMU].tolist(), Y.loc[DMU].tolist()] for DMU in DMUs_Name})
print(f'DEA(AP={AP}) MODEL RUNING...')
def __CCR(self):
for k in self.DMUs:
MODEL = gurobipy.Model()
#MODEL.addVar()函数用于添加单个变量。可以通过设置参数来指定变量的下界（lb）、上界（ub）、类型（vtype）和名称（name）等属性。
#MODEL.addVars()函数用于添加多个变量。可以通过设置参数来指定变量的下界（lb）、上界（ub）、类型（vtype）和名称（name）等属性。
OE, lambdas, s_negitive, s_positive = MODEL.addVar(), MODEL.addVars(self.DMUs), MODEL.addVars(self.m1), MODEL.addVars(self.m2) #addVar()创建一个变量，addVars()创建多个变量
MODEL.update() ## 更新变量环境
MODEL.setObjectiveN(OE, index=0, priority=1) #多目标优化
MODEL.setObjectiveN(-(sum(s_negitive) + sum(s_positive)), index=1, priority=0)
#创建多个常规一次/二次/等式约束
MODEL.addConstrs(
gurobipy.quicksum(lambdas[i] * self.X[i][j] for i in self.DMUs if i != k or not self.AP) + s_negitive[
j] == OE * self.X[k][j] for j in range(self.m1))
MODEL.addConstrs(
gurobipy.quicksum(lambdas[i] * self.Y[i][j] for i in self.DMUs if i != k or not self.AP) - s_positive[
j] == self.Y[k][j] for j in range(self.m2))
MODEL.setParam('OutputFlag', 0)
MODEL.optimize() #执行线性规划模型
self.Result.at[k, ('效益分析', '综合技术效益(CCR)')] = MODEL.objVal
self.Result.at[k, ('规模报酬分析',
'有效性')] = '非 DEA 有效' if MODEL.objVal < 1 else 'DEA 弱有效' if s_negitive.sum().getValue() + s_positive.sum().getValue() else 'DEA 强有效'
self.Result.at[k, ('规模报酬分析',
'类型')] = '规模报酬固定' if lambdas.sum().getValue() == 1 else '规模报酬递增' if lambdas.sum().getValue() < 1 else '规模报酬递减'
for m in range(self.m1):
self.Result.at[k, ('差额变数分析', f'{self.m1_name[m]}')] = s_negitive[m].X
self.Result.at[k, ('投入冗余率', f'{self.m1_name[m]}')] = 'N/A' if self.X[k][m] == 0 else s_negitive[m].X / self.X[k][m]
for m in range(self.m2):
self.Result.at[k, ('差额变数分析', f'{self.m2_name[m]}')] = s_positive[m].X
self.Result.at[k, ('产出不足率', f'{self.m2_name[m]}')] = 'N/A' if self.Y[k][m] == 0 else s_positive[m].X / self.Y[k][m]
return self.Result
def __BCC(self):
for k in self.DMUs:
MODEL = gurobipy.Model()
TE,lambdas = MODEL.addVar(), MODEL.addVars(self.DMUs) #addVar()创建一个变量，addVars()创建多个变量
MODEL.update() ## 更新变量环境
MODEL.setObjective(TE,sense=gurobipy.GRB.MINIMIZE)##单目标优化；目标函数：最小化TE
# 创建约束条件
MODEL.addConstrs(
gurobipy.quicksum(lambdas[i] * self.X[i][j] for i in self.DMUs if i != k or not self.AP) <= TE * self.X[k][j] for j in range(self.m1))
MODEL.addConstrs(
gurobipy.quicksum(lambdas[i] * self.Y[i][j] for i in self.DMUs if i != k or not self.AP) >= self.Y[k][j] for j in range(self.m2))
MODEL.addConstr(gurobipy.quicksum(lambdas[i] for i in self.DMUs if i != k or not self.AP) == 1)
MODEL.setParam('OutputFlag', 0) #求解日志关闭 #去掉计算过程，只取最后结果;
MODEL.optimize() #执行线性规划模型
self.Result.at[
k, ('效益分析', '技术效益(BCC)')] = MODEL.objVal if MODEL.status == gurobipy.GRB.Status.OPTIMAL else 'N/A' #MODEL.objVal输出结果
#MODEL.status == gurobipy.GRB.Status.OPTIMAL 模型是否取得最优解
return self.Result
def dea(self):
columns_Page = ['效益分析'] * 3 + ['规模报酬分析'] * 2 + ['差额变数分析'] * (self.m1 + self.m2) + ['投入冗余率'] * self.m1 + [
'产出不足率'] * self.m2
columns_Group = ['技术效益(BCC)', '规模效益(CCR/BCC)', '综合技术效益(CCR)', '有效性', '类型'] + (self.m1_name + self.m2_name) * 2
self.Result = pd.DataFrame(index=self.DMUs, columns=[columns_Page, columns_Group])
self.__CCR()
self.__BCC()
self.Result.loc[:, ('效益分析', '规模效益(CCR/BCC)')] = self.Result.loc[:, ('效益分析', '综合技术效益(CCR)')] / self.Result.loc[:,
('效益分析',
'技术效益(BCC)')]
return self.Result
def analysis(self, file_name=None):
Result = self.dea()
file_name = r'分析结果.xlsx'
Result.to_excel(file_name, 'DEA数据包络分析报告')
if __name__ == '__main__':
io = r"DEA.xlsx" #读取数据
x = pd.read_excel(io, sheet_name = 0, usecols = [1]) # 导入投入数据
y = pd.read_excel(io, sheet_name = 0, usecols = [2,3,4]) # 导入产出数据
country = pd.read_excel(io, sheet_name = 0, usecols = [0])
data = DEA(DMUs_Name= range(0,30), X=x, Y=y)
data.analysis()
# print(data.dea())
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！