【动手学深度学习】(十一)卷积层

2023-12-13 14:08:19

文章目录

一、从全连接到卷积
二、卷积层
三、代码实现
四、填充和步幅
- 1.填充
- 2.步幅
五、通道
- 1.理论知识
- 2.代码实现
【相关总结】
- torch.nn.Conv2d()
- torch.stack()

一、从全连接到卷积

分类猫和狗的图片

使用一个相机采集图片（12M像素）
RGB图片有36M元素
使用100大小的单隐层MLP，模型有3.6B元素
- 远多于世界上所有猫和狗总数（900M狗，600M猫）
  3.6B要存下来需要14GB内存

两个原则

平移不变性(权值共享)：无论物体在图片中哪个位置，都是这个物体，与其所处位置无关。
局部性：识别物体，只需要这个物体附近的信息即可，不需要整张图片。
不变性

在这里插入图片描述
以上图游戏为例，在这个游戏中包含了许多充斥着活动的混乱场景，而沃尔多通常潜伏在一些不太可能的位置，读者的目标就是找出他。我们可以使用个“沃尔多检测器”扫描图像。该检测器将图像分割成多个区域，并为每个区域包含沃尔多的可能性打分。卷积神经网络正是将空间不变性（spatial invariance）的这一概念系统化，从而基于这个模型使用较少的参数来学习有用的表示。
在进行图像识别时，我们的输入和输出都是图片（需要二维矩阵存储）
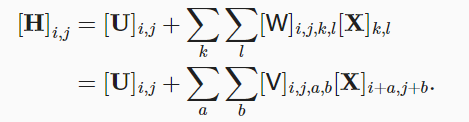
在这里插入图片描述
x:代表输入
h:代表输出矩阵
u:代表偏置
这个四维张量比较难以理解，我们可以先从一维着手去看

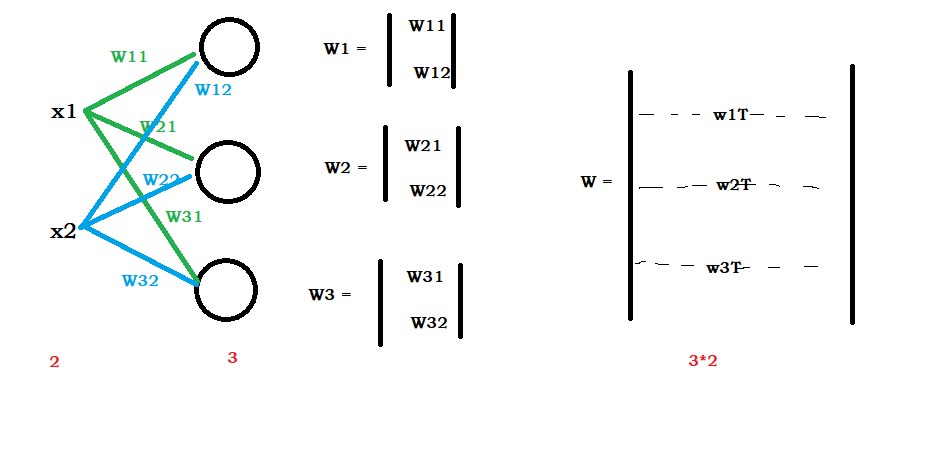
每个输出都与输入有关，所以就是输出w矩阵维度就是输出个数*输入个数
二维同样如此，只是输入和输出都为图片，为了保持空间结构，需要二维矩阵存储。
【总结】：
对全连接层使用平移不变性和局部性得到卷积层
在这里插入图片描述

二、卷积层

1.二维交叉相关
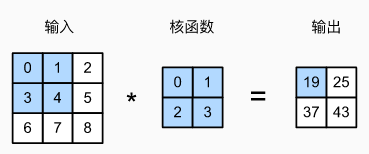
在这里插入图片描述
暂时忽略通道，二维互关运算
00+11+32+34=19
假设输入大小为nhnw,卷积核大小为khhw，那么输出大小为：

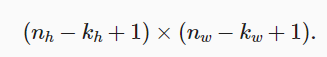
2.二维卷积层

不同的卷积核具有不同的效果
总结：

卷积层将输入和核矩阵进行交叉相关，加上偏移后得到输出
核矩阵和偏移是可学习的参数
核矩阵的大小是超参数

三、代码实现

1.互相关运算

# 互相关运算
import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

# 验证上述运算
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X,K)

tensor([[19., 25.],
[37., 43.]])

2.卷积层

# 实现二维卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
#       卷积核权重
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))
        
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

3.图像中目标的边缘检测

卷积层的简单应用：
通过找到像素变化的位置，检测图像中不同颜色的边缘。

#黑色为0，白色为1
X = torch.ones((6, 8))
X[:, 2:6] = 0
X

tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
构造卷积核K，当进行卷积操作时，如果水平相邻的两元素相同，则输出为0，否则输出非0

K = torch.tensor([[1.0, -1.0]])
# 输出Y中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘
Y = corr2d(X, K)
Y

tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])

如果将输入的二维图像转置，再进行上述卷积操作，那么之前检测到的垂直边缘消失了，所以刚刚那个卷积核K只可以检测垂直边缘，无法检测水平边缘。

corr2d(X.t(), K)   # 上述卷积核不可以检测横向边

tensor([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])

4.学习卷积核

如果只需寻找黑白边缘，那么上面的[1, -1]的边缘检测器可以达到效果。然而，当有了更复杂数值的卷积核，或者连续的卷积层时，我们不可能手动设计滤波器。
我们可以通过输入输出学习卷积核

conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
# print(conv2d.weight)

# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y)**2
    conv2d.zero_grad()
    l.sum().backward()
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'batch {i+1}, loss {l.sum(): .3f}')

batch 2, loss 7.535
batch 4, loss 1.666
batch 6, loss 0.444
batch 8, loss 0.142
batch 10, loss 0.051

# 所学的卷积核的权重张量
conv2d.weight.data.reshape((1,2))

tensor([[ 1.0097, -0.9651]])

四、填充和步幅

1.填充

给定（32*32）输入图像
应用5*5大小的卷积核
- 第1层得到输出大小28*28
- 第7层得到输出大小4*4
更大的卷积核可以更快地减小输出大小
- 形状从nhnw减少到（nh-kh+1）（nw-kw+1）

填充：在输入周围添加额外的行和/列
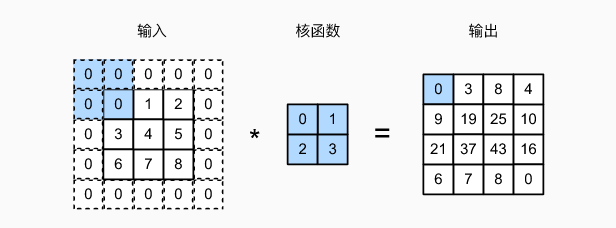
在这里插入图片描述

在这里插入图片描述

2.步幅

填充减小的输出大小与层数线性相关
- 给定输入大小224224，在使用55卷积核的情况下，需要44层将输入降低到4*4
- 需要大量计算才能得到较小输出
步幅是指行/列的滑动的步长

【总结】：
填充和步幅是卷积层的超参数。（参数与超参数的区别：通常参数通常是由数据来驱动调整，超参数则不需要数据来驱动。）
填充在输入周围添加额外的行/列，来控制输出形状的减少量
步幅是每次滑动核窗口时的行/列的步长，可以成倍的减少输出形状

五、通道

1.理论知识

多个输入通道

彩色图像可能有RGB三个通道
转换为灰度会丢失信息
假设我们的输入有多个通道：
每个通道都有一个卷积核，结果是所有通道卷积结果的和。

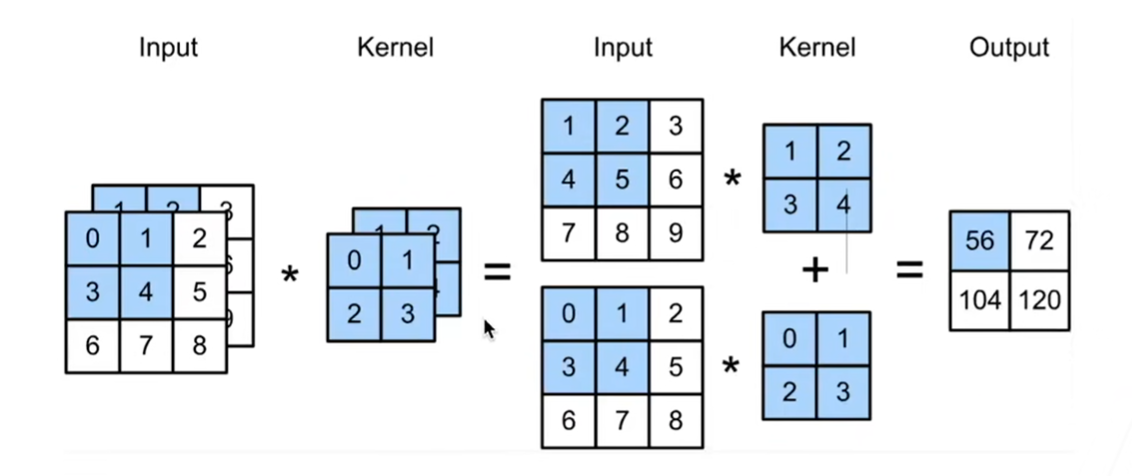
（11+22+43+54）+（00+11+32+43）= 56

多个输出通道

无论有多少输入通道，到目前为止我们只用到单输出通道
我们可以有多个三维卷积核，每个核生成一个输出通道

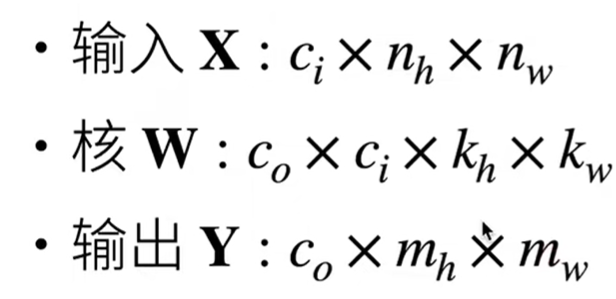
多个输入和输出通道
每个输出通道可以识别特定模式
输入通道核识别并组合输入中的模式

1 * 1卷积层
1*1卷积核不识别空间模式，只是融合通道。
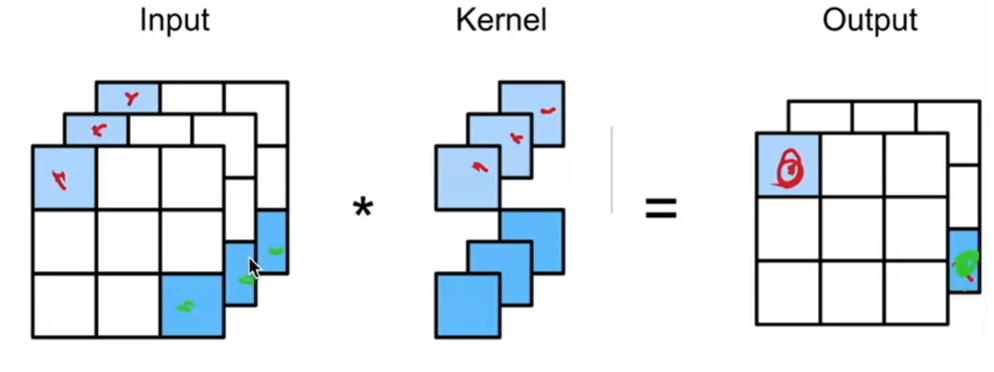
在这里插入图片描述
相当于输入形状为nh * nw * ci,权重为c0 * ci 的全连接层

总结：

输出通道数卷积层的超参数
每个输入通道有独立的二维卷积核，所有通道结果相加得到一个输出通道结果
每个输出通道有独立的三维卷积核

2.代码实现

# 实现一下多输入通道互相关运算

import torch
from d2l import torch as d2l

def corr2d_multi_in(X, K):
#   先遍历X和K的第0个维度（通道维度），再相加
    for x,k in zip(X, K):
#         print(x,k)
        return sum(d2l.corr2d(x,k) for x,k in zip(X,K))

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)

代码解释：
我们实现的是下图的效果：
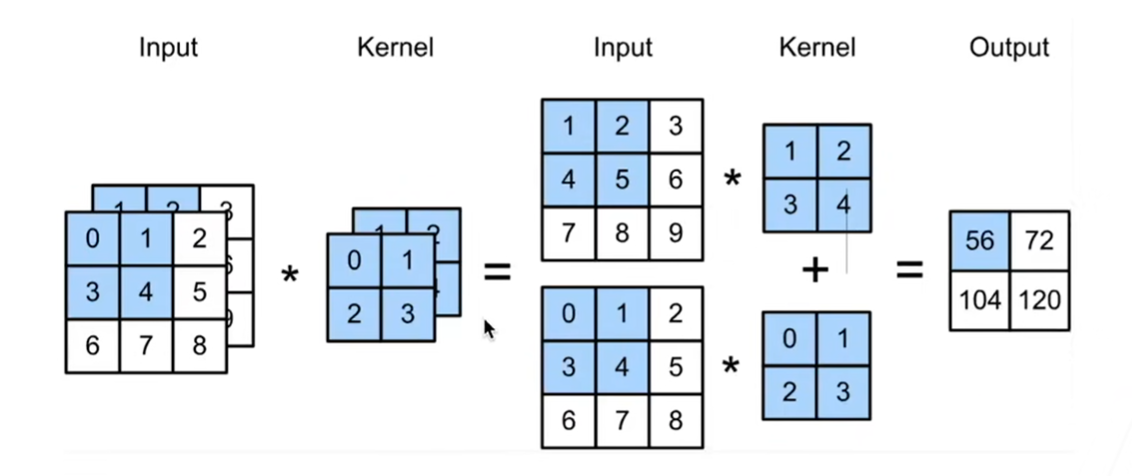
在这里插入图片描述
首先遍历通道数，然后调用d2l.corr2d(x,k)进行卷积操作，最后对两个结果矩阵求和
在遍历中输出卷积结果，进行观察：


def corr2d_multi_in(X, K):
#   先遍历X和K的第0个维度（通道维度），再相加
    for x,k in zip(X, K):
#         print(x,k)
        print(d2l.corr2d(x,k))
#         return sum(d2l.corr2d(x,k) for x,k in zip(X,K))

tensor([[19., 25.],
[37., 43.]])
tensor([[37., 47.],
[67., 77.]])

计算多个通道的输出的互相关函数

# 计算多个通道的输出的互相关函数

def corr2d_multi_in_out(X, K):
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

K = torch.stack((K, K+1, K+2), 0)
K.shape

torch.Size([3, 2, 2, 2])

corr2d_multi_in_out(X, K)

tensor([[[ 56., 72.],
[104., 120.]],

    [[ 76., 100.],
     [148., 172.]],

    [[ 96., 128.],
     [192., 224.]]])

1×1卷积
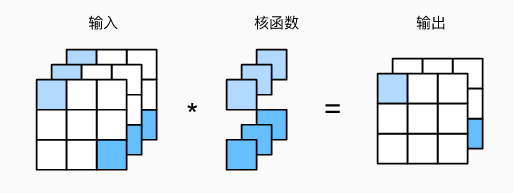
在这里插入图片描述

# 1*1卷积

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
#     print(c_i, h, w)
    c_o = K.shape[0]
#   将输入张量 X 变形为二维矩阵
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
#     print(K.shape)
    print(K)
    
    print(X)
    # 全连接层中的矩阵乘法
    Y = torch.matmul(K, X)
    return Y.reshape((c_o, h, w))

X = torch.normal(0, 1, (3, 3, 3))
# print(X)
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6

【相关总结】

torch.nn.Conv2d()

torch.nn.Conv2d(in_channels, out_channels, kernel_size, [stride=1, padding=0, dilation=1, groups=1, bias=True])

in_channels：输入通道数
out_channels：卷积产生的通道数
kernel_size:卷积核大小

卷积操作的输入需要是一个四维的：
x[ batch_size, channels, height, width ]
卷积操作：
Conv2d[ channels, output, kernel_size ]

channels通道数需要和输入保持一致
kernel_size:卷积核的大小，可以用一个数，也可以分别设置高和宽

输出：
out[ batch_size,output, height, width ]

import torch
from torch import nn

# 定义卷积层
conv2d_layer = nn.Conv2d(in_channels=1, out_channels=64, kernel_size=3, stride=1, padding=1)

x = torch.randn(3, 1, 6, 6)  # 一个大小为 (batch_size, channels, height, width) 的输入张量
# print(x)
# 进行卷积操作，卷积操作的输入应该是四维
output_data = conv2d_layer(x)
# print(output_data)
print(output_data.shape)

torch.Size([3, 64, 6, 6])

torch.stack()

torch.stack 是 PyTorch 中用于在新创建的维度上堆叠（stack）张量序列的函数。具体而言，它将一系列张量沿着一个新的维度堆叠在一起，生成一个新的张量。
torch.stack(tensors, dim=0, *, out=None)

tensors: 一个张量序列，所有张量的形状必须相同。
dim: 沿着哪个维度进行堆叠。新创建的维度将在这个位置。默认是 0。

import torch

# 创建两个张量
x = torch.tensor([1, 2, 3])
y = torch.tensor([4, 5, 6])

# 使用 torch.stack 进行堆叠
stacked_tensor = torch.stack([x, y])
print(stacked_tensor)

tensor([[1, 2, 3],
[4, 5, 6]])

平移不变性

文章来源:https://blog.csdn.net/qq_52986400/article/details/134841840
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！