机器学习---KNN最近邻算法

1、KNN最近邻算法

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一，有监督算法。该方法的思路是：如果一个样本在特征空间中的k个最相似的样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法由你的邻居来推断出你的类别，KNN算法就是用距离来衡量样本之间的相似度。

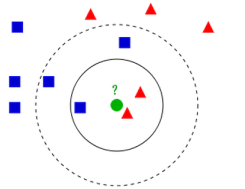
如果K = 3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。

如果K = 5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

K 值的选择，距离度量和分类决策规则是该算法的三个基本要素。K值的选择一般低于样本数据的平方根,一般是不大于20的整数。距离度量常用的有欧式距离，曼哈顿距离，余弦距离等，一般使用欧氏距离，对于文本分类，常用余弦距离。分类决策就是“少数服从多数”的策略。

2、KNN算法步骤

（1）、对于未知类别的数据（对象，点），计算已知类别数据集中的点到该点的距离。

（2）、按照距离由小到大排序

（3）、选取与当前点距离最小的K个点

（4）、确定前K个点所在类别出现的概率

（5）、返回当前K个点出现概率最高的类别作为当前点预测分类

3、KNN算法复杂度

KNN 分类的计算复杂度和训练集中的文档数目成正比，也就是说，如果训练集中文档总数为 n，那么 KNN 的分类时间复杂度为O(n)

4、KNN问题

该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的 K 个邻居中大容量类的样本占多数。解决：可以采用权值的方法，根据和该样本距离的远近，对近邻进行加权，距离越小的邻居权值大，权重一般为距离平方的倒数。

5、KNN数据归一化

为了防止某一维度的数据的数值大小对距离计算产生影响，保证多个维度的特征是等权重的，最终结果不能被数值的大小影响，应该将各个维度进行数据的归一化，把数据归一化到[0,1]区间上。

归一化公式：

6、距离度量

欧式距离：

也称欧几里得距离，在一个N维度的空间里，求两个点的距离，这个距离肯定是一个大于等于零的数字，那么这个距离需要用两个点在各自维度上的坐标相减，平方后加和再开方。一维，二维，三维的欧式距离计算方法：

一维：??

二维：

三维：

平方欧式距离：

就是欧式距离的平方

曼哈顿距离：

相比欧式距离简单的多，曼哈顿距离只要把两个点坐标的x坐标相减取绝对值，y坐标相减取绝对值，再加和，? ,三维，四维以此类推。

余弦距离：

也叫余弦相似度，是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。如果两个向量的方向一致，即夹角接近零，那么这两个向量就越相近。要确定两个向量方向是否一致，要用到余弦定理计算向量的夹角。

闵可夫斯基距离：

闵式距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性表述。定义：两个n维变量（可以理解为n维数组，就是有n个元素）?与间的闵可夫斯基距离定义为：其中p是一个变参数，当p=1时，就是曼哈顿距离，当p=2时，就是欧式距离，当?就是切比雪夫距离。

?就是切比雪夫距离。

切比雪夫距离：

国际象棋中，国王可以直行、横行、斜行。国王走一步，可以移动到相邻的8个方格的任意一个。国王从格子()到格子最少需要多少步？这个距离就是切比雪夫距离。

切比雪夫距离公式简单理解为就是各坐标数值差的最大值，在2维空间中的计算公式为：

谷本距离：

同时考虑余弦距离和欧式距离的测度。

加权距离测度：

可以指定某一维度的权重比例，从而使某个权重的影响力更大。