算法备胎hash和队列的特征——第五关青铜挑战

内容	1.Hash存储方式
	2.Hash处理冲突的方式
	3.队列存储的基本特征
	4.如何使用链表来实现栈

1.Hash 基础

1.1Hash的概念和基本特征

哈希（Hash）也称为散列，就是把任意长度的输入，通过散列算法，变换成固定长度的输出，这个输出值就是散列值。

很多人可能想不明白，这里的映射到底是什么意思 ，为啥访问的时间复杂度为O(1)？

我们只要看存的时候和读的时候分别怎么映射的就知道了。

我们现在假设数组array存放的是1到15这些数字，现在要存在一个大小是7的Hash表中，该如何存储呢？

我们存储的位置计算公式是：

index=number 模7

这个时候我们将1到6存入的时候，如图所示

这个没有疑问吧，就是简单的取模，然后继续7到13，结果就是这样：?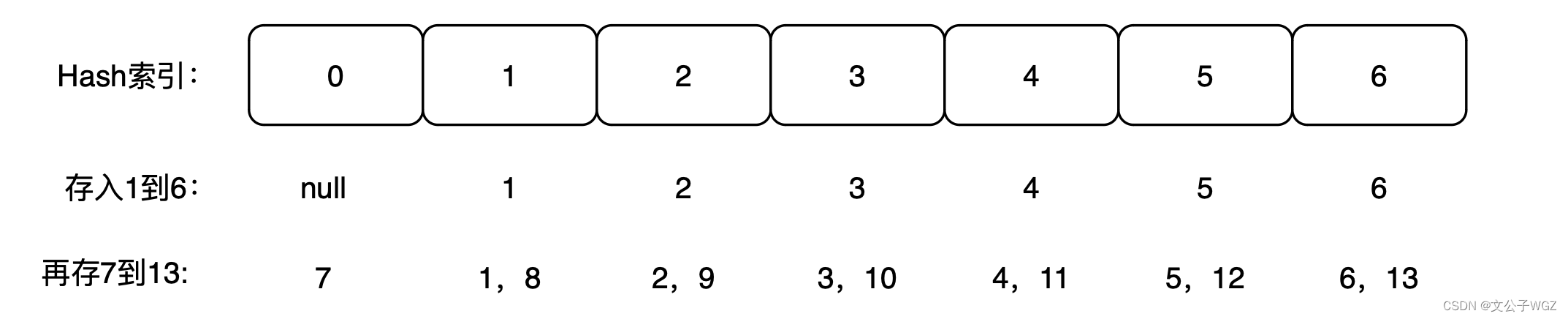

?最后再存14到15: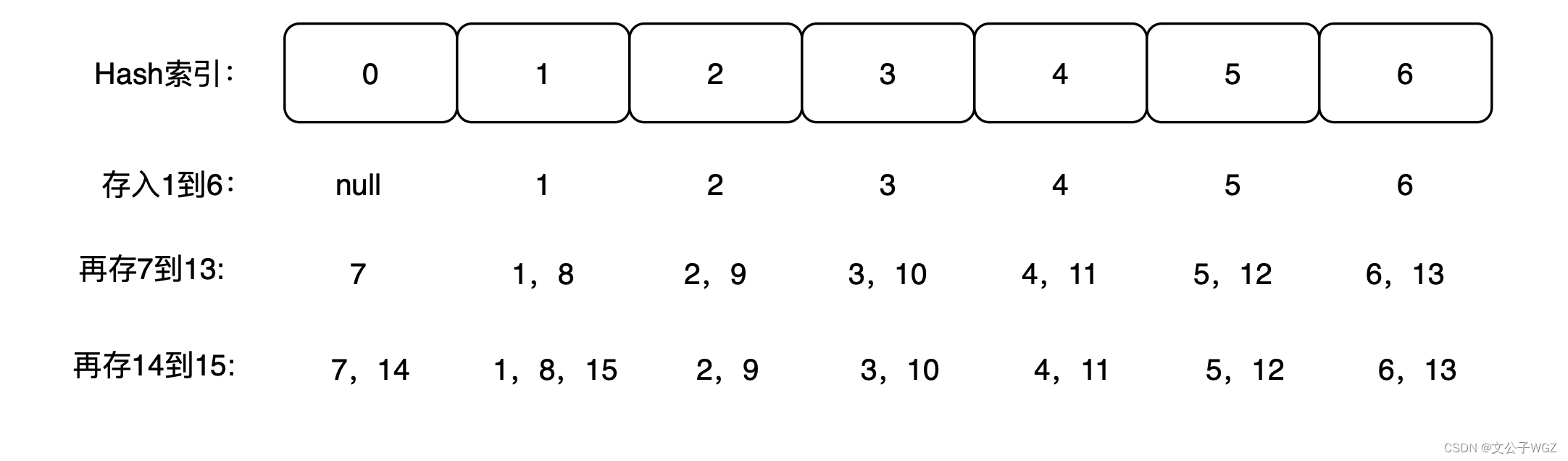

这个时候我们会发现有些数据被存到了同一个位置了。接下来，我们看看如何取出来。

假如我要测试13在不在这个结构里，则同样使用上面的公式来进行，很明显13模7=6.我们直接访问array[6]，我们直接访问array[6]这个位置，很明显是在的，所以返回true。

?假如我要测试20在不在这个结构里，则同样使用上面的公式来进行，很明显20模7=6.我们直接访问array[6]，我们直接访问array[6]这个位置，但是只有6和13，所以返回false。

理解这个例子我们就理解了Hash是如何进行最近基本的映射，还有就是为什么访问的时间复杂度O(1)。

?1.2碰撞处理方法

上面的例子中，我们发现有些在Hash中很多位置可能要存储两个甚至更多个元素，很明显单纯的数组是不行的，这种两个不同的输入值，根据同一散列函数计算出的散列值相同的现象叫做碰撞。

那该怎么解决呢？常见的方法有：

开放定址法(Java里的Threadlocal)、链地址法(Java里的ConcurrentHshMap）、再哈希法（布隆过滤器）、建立公共溢出区。后两者用的比较少，这里着重看前两个。

1.2.1开放地址法

开放地址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

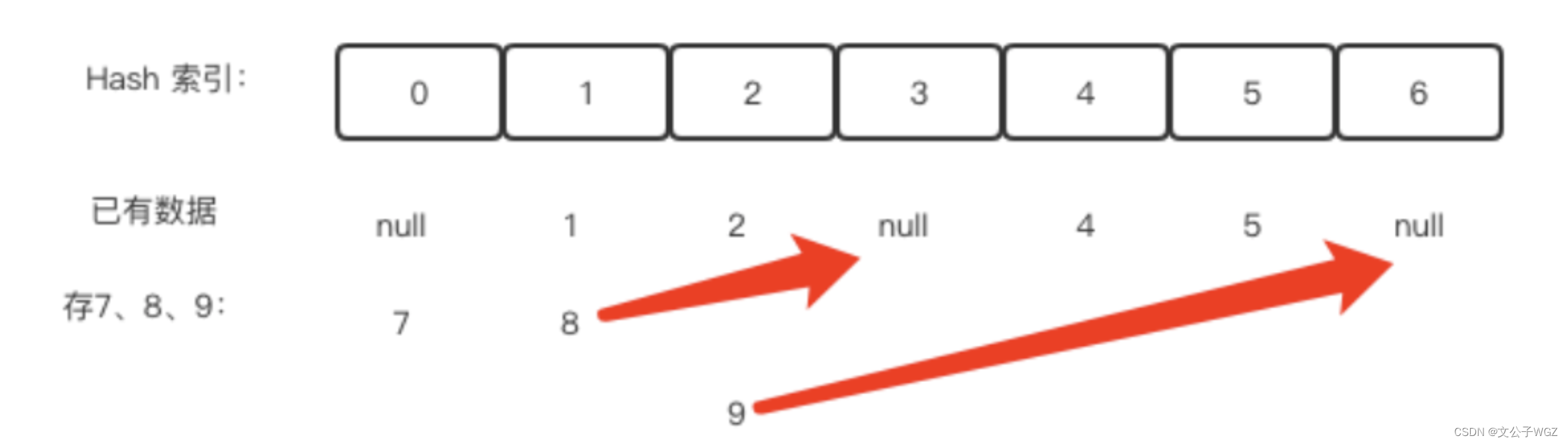
?例如上面7，8，9的时候，7没有问题，就可以直接存到索引为0位置，8本来应该存到索引为1的位置，但是已经满了，所以继续向后找，索引3的位置是空的，所以8存到3的位置，同理9存到索引6位置。

这里 你是否有一个疑惑：这样鸠占鹊巢的方法会不会引起混乱？

比如再存入3和6的话，本来自己的为孩子好好的，但是被外来户占领了，该如何处理呢？

这个问题直到我在学习java里的ThreadLocal才揭开。具体过成可以学习下一个相关内容，我们这里只说一下基本思想。

ThreadLocal有一个专门存入元素的TheadLocalMap，每次在get和set元素的时候，会先将目标位置前后的空间搜索一下，将标记为null的位置回收，这样大部分不用的位置就受回来了。

1.2.2链地址法

将哈希表的每个单元作为链表的头结点，所有哈希地址为i的元素构成一个同义词链表。即发生冲突 时就把该关键字链在以该单元为头结点的链表的尾部。例如：

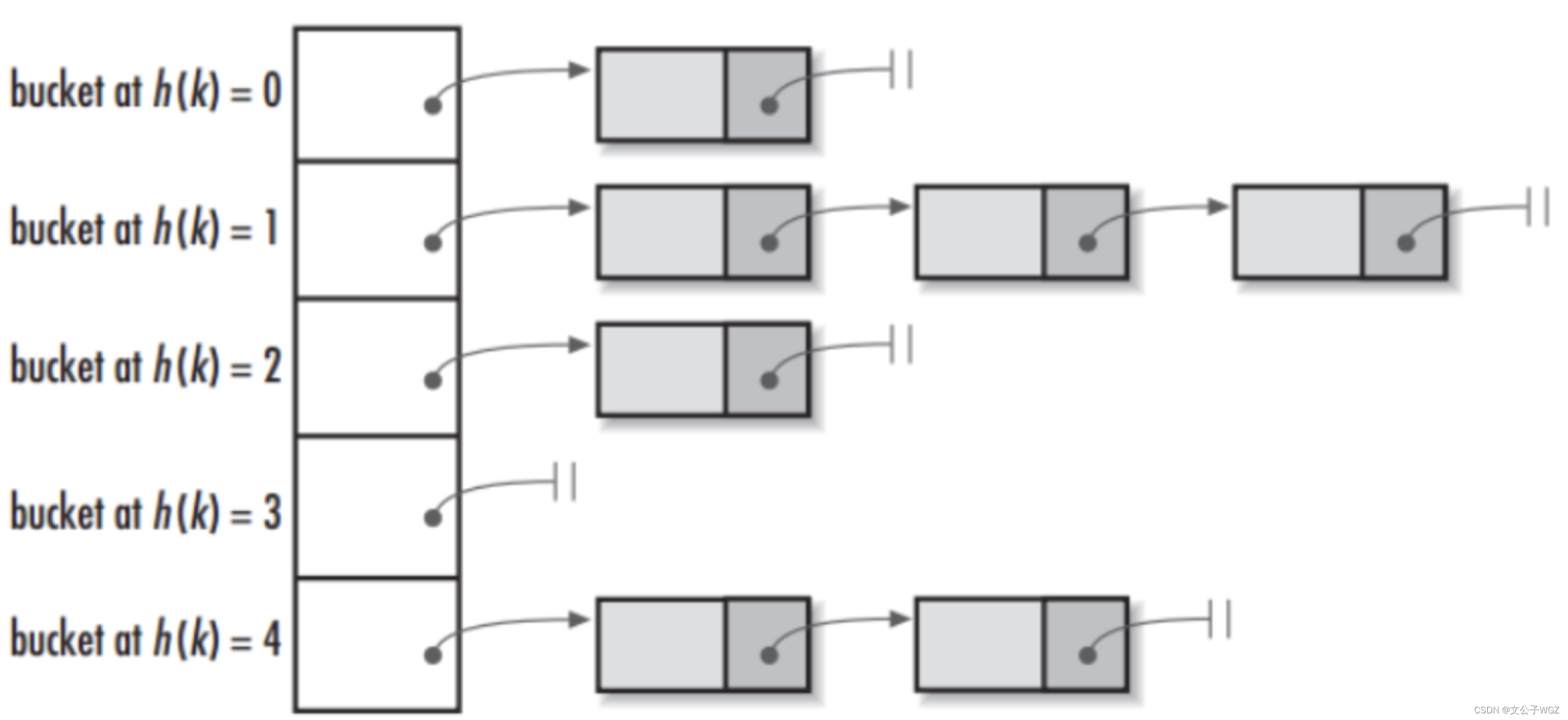
?这种处理方法的问题就是处理起来代价还是比较高的，落地还要进行很多优化，例如在Java里的ConcurrentHashMap中就使用了这种方式，其中涉及元素尽量均匀、访问和操作速度要快、线程安全、扩容等很多问题。

我们来看一下下面这个Hash结构，下面的图有两处非常明显的错误，请你想想是啥

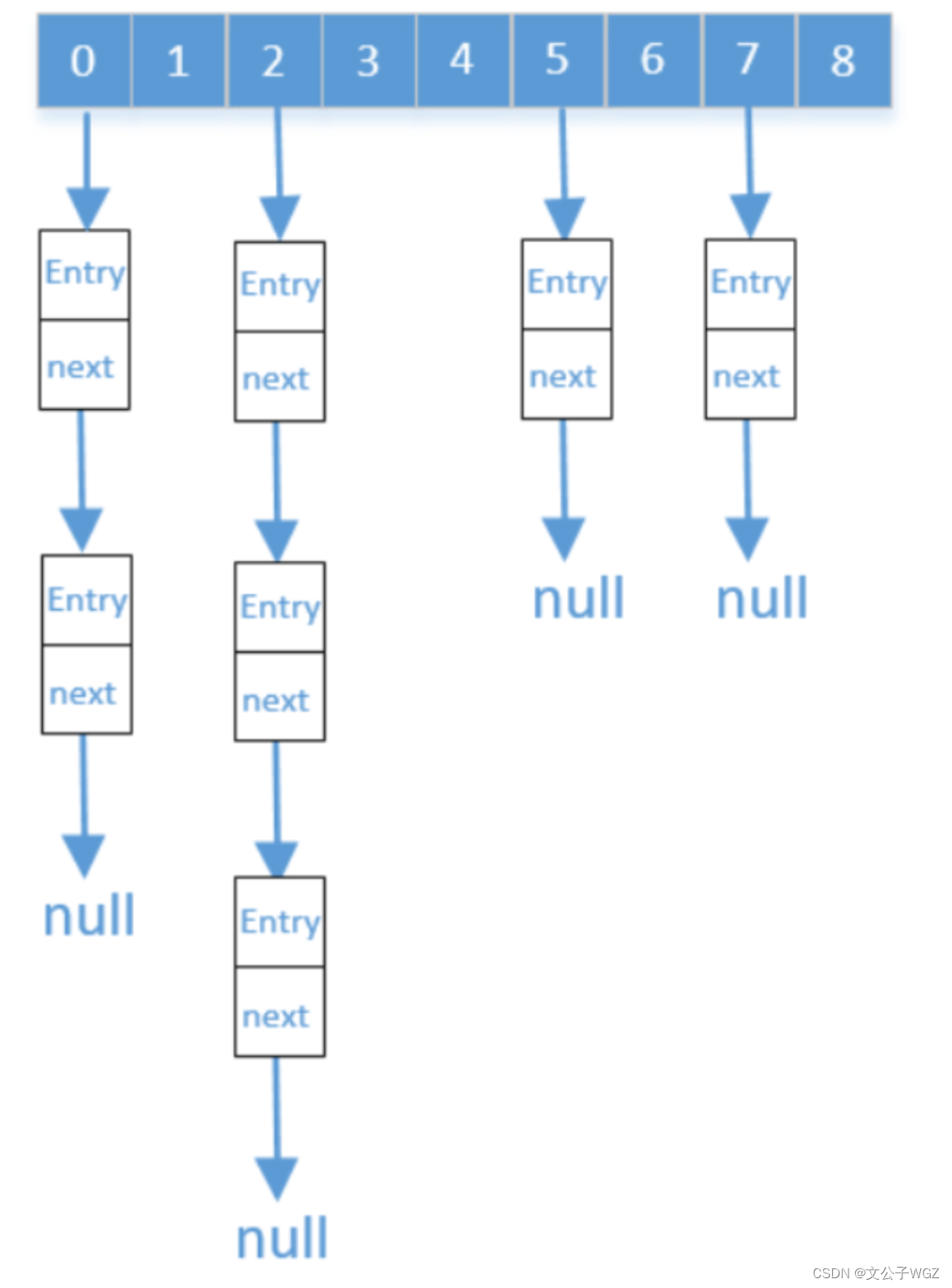
?数组的长度即是2的n次幂，而他的size又不大于数组长度的75%。

HashMap的实现原理是先要找到要存放数组的下标，如果是空的就存进去，如果不是空的就判断key值是否一样，如果一样就替换，如果不一样就以链表的形式存在链表中(从JDK8开始，根据元素数量选择使用链表还是红黑树存储）。

2.队列基础知识

2.1队列的概念和基本特征

队列的特点是节点的排队次序和出队次序按入队时间先后确定，即先入队者先出队，后入队者后出队，即我们常说的FIFO(first in first out)先进先出。

队列实现方式也是两个形式，基于数组和基于链表。对于基于链表，会有点麻烦。我们将其放在黄金挑战里再看，这里只看一下基于链表实现的方法。

2.2实现队列。

?基于链表实现队列还是比较好处理的，只要在尾部后插入元素，在front删除处元素就行了。

package com.yugutou.charpter5_queue_map.level1;

public class LinkQueue {
    private Node front; // 队头指针
    private Node rear;  // 队尾指针
    private int size;   // 队列中元素个数

    public LinkQueue() {
        this.front = new Node(0);  // 构造函数中初始化队头指针
        this.rear = new Node(0);   // 构造函数中初始化队尾指针
    }

    /**
     * 入队
     */
    public void push(int value) {
        Node newNode = new Node(value); // 创建一个新节点
        Node temp = front;              // 从队头开始遍历队列，寻找最后一个节点
        while (temp.next != null) {
            temp = temp.next;
        }
        temp.next = newNode; // 将新节点插入到队尾
        rear = newNode;      // 更新队尾指针
        size++;
    }

    /**
     * 出队
     */
    public int pull() {
        if (front.next == null) {
            System.out.println("队列已空");
        }
        Node firstNode = front.next; // 找到队头节点
        front.next = firstNode.next; // 将队头指针指向下一个节点
        size--;
        return firstNode.data; // 返回队头节点的值
    }

    /**
     * 遍历队列
     */
    public void traverse() {
        Node temp = front.next; // 从队头节点开始遍历队列
        while (temp != null) {
            System.out.print(temp.data + "\t"); // 打印节点的值
            temp = temp.next; // 移动指针到下一个节点
        }
    }

    static class Node {
        public int data;  // 节点的值
        public Node next; // 指向下一个节点的指针

        public Node(int data) {
            this.data = data;
        }
    }

    // 测试main方法
    public static void main(String[] args) {
        LinkQueue linkQueue = new LinkQueue(); // 创建队列对象
        linkQueue.push(1); // 向队列中添加元素
        linkQueue.push(2);
        linkQueue.push(3);
        System.out.println("第一个出队的元素为:" + linkQueue.pull()); // 从队列中取出第一个元素
        System.out.println("队列中的元素为:");
        linkQueue.traverse(); // 遍历队列并打印所有元素
    }
}