并行进位加法器
前言
在文章逻辑运算加法器中,介绍了两种加法运算方式,串行进位加法器和进位选择加法器,我们给出了逻辑门的实现并给出了C语言描述,本篇文章介绍另外一种加法计算方法:并行进位加法器
写在前面
- 使用 ? \bigoplus ?表示异或
- 使用 + + +号表示或
- AB表示A与B
门延迟
首先介绍一个概念,门延迟。
我们知道,集成电路的主要工作单位是晶体管,晶体管虽然状态的改变非常迅速,但是毕竟有延迟,尤其随着晶体管串行数量的增大,延迟不可小觑。我们把一组电路中最大串行逻辑门的延迟门数量之和称为该电路的延迟门。延迟门是衡量电路性能的标志,下面是基本逻辑门的延迟门数量:
- 与门,非门,或门延迟门设置为1
- 与非门,或非门延迟门设置为2
- 异或门延迟门设置为3,因为异或门是
使用一个或门,一个与非门进行与门操作实现的。
并行进位加法器
全先行进位加法
我们从前面的文章能知道,串行进位加法器的主要性能瓶颈在于每一项的进位值需要前面的计算结果。对于n位的两个相加的值
X
X
X和
Y
Y
Y,我们再次给出进位值和计算值的公式:
{
F
i
=
(
X
i
?
Y
i
)
?
C
i
?
1
,
计算值
C
i
=
(
X
i
C
i
?
1
)
+
(
Y
i
C
i
?
1
)
+
(
X
i
Y
i
)
,
进位值
\begin{cases} F_i = (X_i \bigoplus Y_i) \bigoplus C_{i-1},计算值\\ C_i = (X_i C_{i-1}) + (Y_i C_{i-1}) + (X_i Y_i ),进位值 \end{cases}
{Fi?=(Xi??Yi?)?Ci?1?,计算值Ci?=(Xi?Ci?1?)+(Yi?Ci?1?)+(Xi?Yi?),进位值?
用电路表示
F
i
F_i
Fi?的值为:
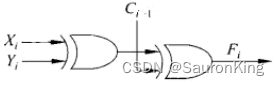
用电路表示
C
i
C_i
Ci?的值为,可以看到进位的计算的门延迟是2:
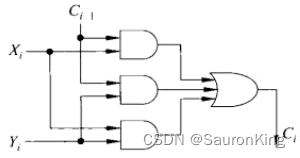
根据布尔运算
C
i
=
(
X
i
C
i
?
1
)
+
(
Y
i
C
i
?
1
)
+
(
X
i
Y
i
)
=
X
i
Y
i
+
(
X
i
+
Y
i
)
C
i
?
1
C_i =(X_i C_{i-1}) + (Y_i C_{i-1}) + (X_i Y_i ) = X_i Y_i + (X_i+Y_i)C_{i-1}
Ci?=(Xi?Ci?1?)+(Yi?Ci?1?)+(Xi?Yi?)=Xi?Yi?+(Xi?+Yi?)Ci?1?
也就是说:
C
1
=
X
1
Y
1
+
(
X
1
+
Y
1
)
C
0
C_1 = X_1 Y_1 + (X_1+Y_1)C_{0}
C1?=X1?Y1?+(X1?+Y1?)C0?
C
2
=
X
2
Y
2
+
(
X
2
+
Y
2
)
C
1
=
X
2
Y
2
+
(
X
2
+
Y
2
)
(
X
1
Y
1
+
(
X
1
+
Y
1
)
C
0
)
=
X
2
Y
2
+
(
X
2
+
Y
2
)
(
X
1
Y
1
)
+
(
X
2
+
Y
2
)
(
X
1
+
Y
1
)
C
0
\begin{aligned} C_2 &= X_2 Y_2 + (X_2+Y_2)C_{1}\\ &=X_2 Y_2 + (X_2+Y_2)(X_1 Y_1 + (X_1+Y_1)C_{0})\\ &=X_2 Y_2 + (X_2+Y_2)(X_1 Y_1) + (X_2+Y_2)(X_1+Y_1)C_{0} \end{aligned}
C2??=X2?Y2?+(X2?+Y2?)C1?=X2?Y2?+(X2?+Y2?)(X1?Y1?+(X1?+Y1?)C0?)=X2?Y2?+(X2?+Y2?)(X1?Y1?)+(X2?+Y2?)(X1?+Y1?)C0??
C
3
=
X
3
Y
3
+
(
X
3
+
Y
3
)
C
2
=
X
3
Y
3
+
(
X
3
+
Y
3
)
(
X
2
Y
2
+
(
X
2
+
Y
2
)
(
X
1
Y
1
)
+
(
X
2
+
Y
2
)
(
X
1
+
Y
1
)
C
0
)
=
X
3
Y
3
+
(
X
3
+
Y
3
)
(
X
2
Y
2
)
+
(
X
3
+
Y
3
)
(
X
2
+
Y
2
)
(
X
1
Y
1
)
+
(
X
3
+
Y
3
)
(
X
2
+
Y
2
)
(
X
1
+
Y
1
)
C
0
\begin{aligned} C_3 &= X_3 Y_3 + (X_3+Y_3)C_{2}\\ &=X_3 Y_3 + (X_3+Y_3)(X_2 Y_2 + (X_2+Y_2)(X_1 Y_1) + (X_2+Y_2)(X_1+Y_1)C_{0})\\ &=X_3 Y_3 + (X_3+Y_3)(X_2 Y_2) + (X_3+Y_3)(X_2+Y_2)(X_1 Y_1)+(X_3+Y_3)(X_2+Y_2)(X_1+Y_1)C_{0} \end{aligned}
C3??=X3?Y3?+(X3?+Y3?)C2?=X3?Y3?+(X3?+Y3?)(X2?Y2?+(X2?+Y2?)(X1?Y1?)+(X2?+Y2?)(X1?+Y1?)C0?)=X3?Y3?+(X3?+Y3?)(X2?Y2?)+(X3?+Y3?)(X2?+Y2?)(X1?Y1?)+(X3?+Y3?)(X2?+Y2?)(X1?+Y1?)C0??
我们假设
P
i
=
X
i
+
Y
i
P_i = X_i+Y_i
Pi?=Xi?+Yi?,
G
i
=
X
i
Y
i
G_i = X_iY_i
Gi?=Xi?Yi?,也就是
P
i
P_i
Pi?是一个逻辑或门,
G
i
G_i
Gi?是一个逻辑与门,上面的公式可以写成如下形式:
C
1
=
G
1
+
P
1
C
0
C_1 = G_1 + P_1C_{0}
C1?=G1?+P1?C0?
C
2
=
G
2
+
P
2
G
1
+
P
2
P
1
C
0
C_2= G_2 + P_2G_1+ P_2P_1C_{0}
C2?=G2?+P2?G1?+P2?P1?C0?
C
3
=
G
3
+
P
3
G
2
+
P
3
P
2
G
1
+
P
3
P
2
P
1
C
0
C_3= G_3 + P_3G_2+P_3P_2G_1+P_3P_2P_1C_{0}
C3?=G3?+P3?G2?+P3?P2?G1?+P3?P2?P1?C0?
同理:
C
4
=
G
4
+
P
4
G
3
+
P
4
P
3
G
2
+
P
4
P
3
P
2
G
1
+
P
4
P
3
P
2
P
1
C
0
C_4= G_4 + P_4G_3+P_4P_3G_2+P_4P_3P_2G_1+P_4P_3P_2P_1C_{0}
C4?=G4?+P4?G3?+P4?P3?G2?+P4?P3?P2?G1?+P4?P3?P2?P1?C0?
即然
C
4
、
C
3
、
C
2
、
C
1
C_4、C_3、C_2、C_1
C4?、C3?、C2?、C1?都能使用
C
0
C_0
C0?来表示,那么我们就可以通过设计电路来同时计算
C
4
、
C
3
、
C
2
、
C
1
C_4、C_3、C_2、C_1
C4?、C3?、C2?、C1?的值,然后根据计算后的值进行每一位的加法运算。设计后电路图如下:
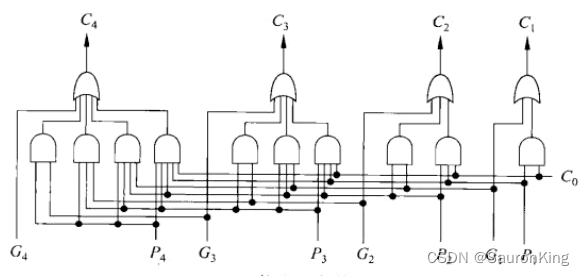
上面的电路称为先行进位部件,简称CLA(Carry Lookahead Unit)
我们把输入的
X
、
Y
X、Y
X、Y和数值位的计算添加进来,然后把
C
i
C_i
Ci?的值也添加到加法器,这样便组成了一个全先行进位加法,电路图如下:
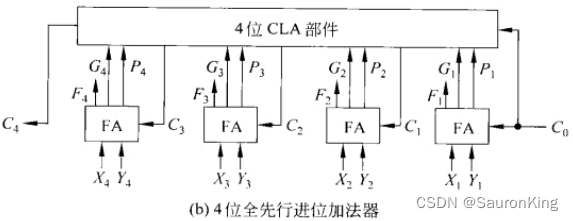
我们看一下上面电路的门延迟:
- X i 、 Y i X_i、Y_i Xi?、Yi?输入后需要计算 G i 、 P i G_i、P_i Gi?、Pi?,因为可以并行计算,门延迟数为1
- G i 、 P i G_i、P_i Gi?、Pi?与 C i ? 1 C_{i-1} Ci?1?开始计算 C i C_i Ci?,根据CLA的电路图,需要门延迟数为2
- 这个时候步骤1与步骤2共需要门延迟为3,巧的是,这两步执行过程过程中,数值位也在
并行着,并且 M i = X i ? Y i M_i = X_i \bigoplus Y_i Mi?=Xi??Yi?异或操作门延迟正好也是3,也就是到现在为止,一共的门延迟为3 - 然后开始计算
M
i
?
C
i
M_i \bigoplus C_i
Mi??Ci?异或操作,门延迟为3,加上之前的操作,
所有的门延迟一共为6
下面,给出CLA电路的C语言描述:
/**
* CLA电路的C语言描述,计算4位的加法值
* in_1:输入X
* in_2:输入Y
* c0:默认的进位项
*/
extern long alu_add_cla(long in_1, long in_2, long* c0);
long alu_add_cla(long in_1, long in_2, long* c0)
{
// 初始结果为0
long result = 0;
// 下面这四组并行,每一组在电路中需要1级门延迟
long x1 = alu_bit(in_1, 0); // 获取输入1的第0位
long y1 = alu_bit(in_2, 0); // 获取输入2的第0位
long p1 = or_gate(x1, y1);
long g1 = and_gate(x1, y1);
long x2 = alu_bit(in_1, 1); // 获取输入1的第1位
long y2 = alu_bit(in_2, 1); // 获取输入2的第1位
long p2 = or_gate(x2, y2);
long g2 = and_gate(x2, y2);
long x3 = alu_bit(in_1, 2); // 获取输入1的第2位
long y3 = alu_bit(in_2, 2); // 获取输入2的第2位
long p3 = or_gate(x3, y3);
long g3 = and_gate(x3, y3);
long x4 = alu_bit(in_1, 3); // 获取输入1的第3位
long y4 = alu_bit(in_2, 3); // 获取输入2的第3位
long p4 = or_gate(x4, y4);
long g4 = and_gate(x4, y4);
// CLA电路实现,需要门延迟2
long c1 = or_gate(g1, and_gate(p1, *c0));
long c2 = or_gate(or_gate(g2, and_gate(p2, g1)),and_gate(and_gate(p2, p1), *c0));
long c3 = or_gate(or_gate(or_gate(g3, and_gate(p3, g2)), and_gate(and_gate(p3, p2), g1)), and_gate(and_gate(and_gate(p3, p2), p1), *c0));
long c4 = or_gate(or_gate(or_gate(or_gate(g4, and_gate(p4, g3)), and_gate(and_gate(p4, p3), g2)), and_gate(and_gate(and_gate(p4, p3), p2), g1)), and_gate(and_gate(and_gate(and_gate(p4, p3), p2), p1), *c0));
// 异或操作,门延迟3,与上面的并行
long m1 = xor_gate(x1, y1);
long m2 = xor_gate(x2, y2);
long m3 = xor_gate(x3, y3);
long m4 = xor_gate(x4, y4);
// 最后的异或计算,门延迟3
long r1 = xor_gate(m1, *c0);
long r2 = xor_gate(m2, c1);
long r3 = xor_gate(m3, c2);
long r4 = xor_gate(m4, c3);
result |= r4<<3;
result |= r3<<2;
result |= r2<<1;
result |= r1;
// 将进位值返回给c0
*c0 = c4;
return result;
}
有了四位的全先行进位加法器我们可以实现多位的加法器了,这里还可以分为两种:
- 单级先行进位加法器
- 多级先行进位加法器
单级先行进位加法器
首先看第一种:
单级先行进位加法器是将
n
n
n个全先行进位加法器串起来,可以实现
4
n
4n
4n位的加法运算,我们计算一下对于
4
n
4n
4n位的单级先行进位加法器,门延迟是多少?
- 每一个全先行进位加法器需要前面一个CLA的 C C C输出,第一个CLA的输出为 C 4 C_4 C4?,我们从前面的介绍很容易计算出从开始到 C 4 C_4 C4?输出需要门延迟为3,其中计算 P P P和 G G G占1,计算 C C C占2,也就是3个门延迟之后,第二个全先行进位加法器可以开始了
- 要知道,这时候所有的全先行进位加法器的 P P P和 G G G都在第1步的时候并发完成了,所以,后面的所有全先行进位加法器的 C C C输出都消耗2个门延迟。
- 所以到最后一个全先行进位加法器获取到上一个CLA的 C C C输入时,一共消耗2n-1个门延迟。然后开始计算最后一个全先行进位加法器的数值位,要注意,最后一个全先行进位加法器的数值位计算完成时,前面所有的全先行进位加法器的数值位都应该计算完成了,因为他们都是并行的。
- 最后一个数值位的计算和最终输出的进位同时进行,一共消耗3个门延迟,
一共消耗2n+2个门延迟
下面这是一个16位的加法器示意图:
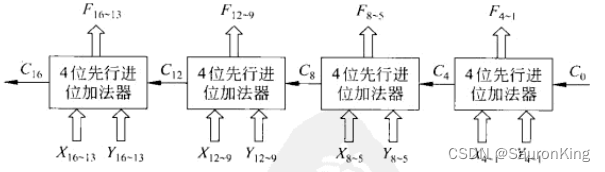
现在我们可以给出64位加法器的C语言描述了,因为有了之前CLA的定义,非常简单:
/**
* CLA电路的串行加法器
* in_1:输入X
* in_2:输入Y
* bits:计算的位数
* c0:默认的进位项
*/
extern long alu_add_cla_64(long in_1, long in_2,long bits, long* c0);
long alu_add_cla_64(long in_1, long in_2,long bits, long* c0)
{
long result = 0;
for(int i = 0;i<bits;i+=4)
{
result |= alu_add_cla(in_1>>i,in_2>>i,c0)<<i;
}
return result;
}
int main(int argc, const char * argv[])
{
int c= 0;
long r0 = alu_add_cla_64(-398, 283, 64, &c);
printf("r0 = %ld\n",r0);
long r1 = alu_add_cla_64(398, 283, 64, &c);
printf("r1 = %ld\n",r1);
}
输出结果为:
r0 = -115
r1 = 681
多级先行进位加法器
最后,我们在研究一下多级先行进位加法器,所谓多级先行进位加法器就是将多个全先行进位加法器并起来,而不是串起来,先看一下16位的两级先行进位加法器,整个逻辑是下面这个样子:
- 四个全先行进位加法器分别同时执行四位的与操作和或操作,获取 P P P和 G G G,这步消耗1个门延迟
- 然后通过与门和或门操作获取
P
m
i
P_{mi}
Pmi?和
G
m
i
,
i
G_{mi},i
Gmi?,i是指的当前全先行进位加法器的索引,
P
m
P_m
Pm?和
G
m
G_m
Gm?是这样一种定义(这步消耗2个门延迟)
P m 1 = P 4 P 3 P 2 P 1 G m 1 = G 4 + P 4 G 3 + P 4 P 3 G 2 + P 4 P 3 P 2 G 1 \begin{aligned} P_{m1}&=P_4P_3P_2P_1\\ G_{m1}&=G_4+P_4G_3+P_4P_3G_2+P_4P_3P_2G_1 \end{aligned} Pm1?Gm1??=P4?P3?P2?P1?=G4?+P4?G3?+P4?P3?G2?+P4?P3?P2?G1?? - 然后开始计算
C
C
C的值,因为我们之前知道全先行进位加法器怎么根据输入的
C
C
C计算四位的输出
C
C
C。现在的问题就是如何同时获取每个全先行进位加法器的输入
C
C
C,即获取
C
4
C_4
C4?、
C
8
C_8
C8?、
C
12
C_{12}
C12?、
C
16
C_{16}
C16?,参考之前的实现,我们可以用下面的方式实现,这一步消耗2个门延迟:
C 4 = G m 1 + P m 1 C 0 C 8 = G m 2 + P m 2 G m 1 + P m 2 P m 1 C 0 C 12 = G m 3 + P m 3 G m 2 + P m 3 P m 2 G m 1 + P m 3 P m 2 P m 1 C 0 C 16 = G m 4 + P m 4 G m 3 + P m 4 P m 3 G m 2 + P m 4 P m 3 P m 2 G m 1 + P m 4 P m 3 P m 2 P m 1 C 0 \begin{aligned} &C_4=G_{m1}+P_{m1}C_0\\ &C_8=G_{m2}+P_{m2}G_{m1}+P_{m2}P_{m1}C_0\\ &C_{12}=G_{m3}+P_{m3}G_{m2}+P_{m3}P_{m2}G_{m1}+P_{m3}P_{m2}P_{m1}C_0\\ &C_{16}=G_{m4}+P_{m4}G_{m3}+P_{m4}P_{m3}G_{m2}+P_{m4}P_{m3}P_{m2}G_{m1}+P_{m4}P_{m3}P_{m2}P_{m1}C_0\\ \end{aligned} ?C4?=Gm1?+Pm1?C0?C8?=Gm2?+Pm2?Gm1?+Pm2?Pm1?C0?C12?=Gm3?+Pm3?Gm2?+Pm3?Pm2?Gm1?+Pm3?Pm2?Pm1?C0?C16?=Gm4?+Pm4?Gm3?+Pm4?Pm3?Gm2?+Pm4?Pm3?Pm2?Gm1?+Pm4?Pm3?Pm2?Pm1?C0?? - 这一步就跟之前的全先行进位加法器一样了,因为四个输入 C C C都已经获取到了,从这一步到计算全部完成需要2+3个门延迟,2是为了计算全先行进位加法器中的每个 C C C值,3是最后的那步异或操作。
下面给出16位两级先行进位加法器的电路图:

好了,了解了两级先行进位加法器以后,就可以构建三级的先行进位加法器。三级能够进行64位的加减操作,对于我们目前来说足够了,并且三级的并行操作能使性能达到最优。
三级的先行进位加法器构建如下:
- 首先有16个4位先行进位加法器
- 然后16个4位先行进位加法器把
P
m
i
P_{mi}
Pmi?和
G
m
i
G_{mi}
Gmi?传递给4位的BCLA部件,应该有4个BCLA部件,然后,还是根据下面的公式,构建第三层4位的BCLA部件
P m 1 = P 4 P 3 P 2 P 1 G m 1 = G 4 + P 4 G 3 + P 4 P 3 G 2 + P 4 P 3 P 2 G 1 不过公式应该换成 P m m 1 = P m 4 P m 3 P m 2 P m 1 G m m 1 = G m 4 + P m 4 G m 3 + P m 4 P m 3 G m 2 + P m 4 P m 3 P m 2 G m 1 \begin{aligned} P_{m1}&=P_4P_3P_2P_1\\ G_{m1}&=G_4+P_4G_3+P_4P_3G_2+P_4P_3P_2G_1\\ 不过公式应该换成\\ P_{mm1}&=P_{m4}P_{m3}P_{m2}P_{m1}\\ G_{mm1}&=G_{m4}+P_{m4}G_{m3}+P_{m4}P_{m3}G_{m2}+P_{m4}P_{m3}P_{m2}G_{m1}\\ \end{aligned} Pm1?Gm1?不过公式应该换成Pmm1?Gmm1??=P4?P3?P2?P1?=G4?+P4?G3?+P4?P3?G2?+P4?P3?P2?G1?=Pm4?Pm3?Pm2?Pm1?=Gm4?+Pm4?Gm3?+Pm4?Pm3?Gm2?+Pm4?Pm3?Pm2?Gm1?? - 现在相当于先计算第三层的BCLA,根据 P m m i P_{mmi} Pmmi?和 G m m i G_{mmi} Gmmi?和 C 0 C_0 C0?能够计算出 C 16 C_{16} C16?、 C 32 C_{32} C32?、 C 48 C_{48} C48?和 C 64 C_{64} C64?
- 根据 P m i P_{mi} Pmi?和 G m i G_{mi} Gmi?和 C 0 C_0 C0?能够计算出 C 4 C_4 C4?、 C 8 C_8 C8?、 C 12 C_{12} C12?
- 根据 P m i P_{mi} Pmi?和 G m i G_{mi} Gmi?和 C 16 C_{16} C16?能够计算出 C 20 C_{20} C20?、 C 24 C_{24} C24?、 C 28 C_{28} C28?
- 根据 P m i P_{mi} Pmi?和 G m i G_{mi} Gmi?和 C 32 C_{32} C32?能够计算出 C 36 C_{36} C36?、 C 40 C_{40} C40?、 C 44 C_{44} C44?
- 根据 P m i P_{mi} Pmi?和 G m i G_{mi} Gmi?和 C 48 C_{48} C48?能够计算出 C 52 C_{52} C52?、 C 56 C_{56} C56?、 C 60 C_{60} C60?
- 到现在为止,剩下的就使计算具体的每个 C C C值了,应该很熟悉了。
最后,给出三级先行进位加法器的C语言描述,代码比较多,为了展示电路级别的操作,逻辑写的比较复杂,其实实际上很多操作都是并行触发的
/**
* 三级先行进位加法器
* in_1:输入X
* in_2:输入Y
* bits:计算的位数
* c0:默认的进位项
* return:返回计算结果
*/
extern long alu_add_bcla_64(long in_1, long in_2,long bits, long* c0);
long alu_add_bcla_64(long in_1, long in_2,long bits, long* c0)
{
// 计算p、g,一共64位
long out_p = alu_or(in_1, in_2,sizeof(long)*8);
long out_g = alu_and(in_1, in_2,sizeof(long)*8);
// 第二级p、g,一共16位
long out_pm=0;
long out_gm=0;
// 第三极p、g,一共4位
long out_pm2=0;
long out_gm2=0;
// 计算第二级p、g,应该是并行的
for(int i=0;i<16;i++)
{
long p4 =alu_bit(out_p,i*4+3);
long p3 =alu_bit(out_p,i*4+2);
long p2 =alu_bit(out_p,i*4+1);
long p1 =alu_bit(out_p,i*4+0);
long g4 =alu_bit(out_g,i*4+3);
long g3 =alu_bit(out_g,i*4+2);
long g2 =alu_bit(out_g,i*4+1);
long g1 =alu_bit(out_g,i*4+0);
out_pm|=((and_gate(and_gate(and_gate(p4, p3), p2), p1))<<i);
out_gm|=((or_gate(or_gate(or_gate(g4, and_gate(p4, g3)), and_gate(and_gate(p4, p3), g2)), and_gate(and_gate(and_gate(p4, p3), p2), g1)))<<i);
}
// 计算第三极p、g,应该是并行的
for(int i=0;i<4;i++)
{
long p4 =alu_bit(out_pm,i*4+3);
long p3 =alu_bit(out_pm,i*4+2);
long p2 =alu_bit(out_pm,i*4+1);
long p1 =alu_bit(out_pm,i*4+0);
long g4 =alu_bit(out_gm,i*4+3);
long g3 =alu_bit(out_gm,i*4+2);
long g2 =alu_bit(out_gm,i*4+1);
long g1 =alu_bit(out_gm,i*4+0);
out_pm2|=((and_gate(and_gate(and_gate(p4, p3), p2), p1))<<i);
out_gm2|=((or_gate(or_gate(or_gate(g4, and_gate(p4, g3)), and_gate(and_gate(p4, p3), g2)), and_gate(and_gate(and_gate(p4, p3), p2), g1)))<<i);
}
// 根据第三极p、g和c0计算c16、c32、c48、c64,应该是并行的
long p4 =alu_bit(out_pm2,3);
long p3 =alu_bit(out_pm2,2);
long p2 =alu_bit(out_pm2,1);
long p1 =alu_bit(out_pm2,0);
long g4 =alu_bit(out_gm2,3);
long g3 =alu_bit(out_gm2,2);
long g2 =alu_bit(out_gm2,1);
long g1 =alu_bit(out_gm2,0);
long c16 = or_gate(g1, and_gate(p1, *c0));
long c32 = or_gate(or_gate(g2, and_gate(p2, g1)),and_gate(and_gate(p2, p1), *c0));
long c48 = or_gate(or_gate(or_gate(g3, and_gate(p3, g2)), and_gate(and_gate(p3, p2), g1)), and_gate(and_gate(and_gate(p3, p2), p1), *c0));
// c64是最终输出的c0
long c64 = or_gate(or_gate(or_gate(or_gate(g4, and_gate(p4, g3)), and_gate(and_gate(p4, p3), g2)), and_gate(and_gate(and_gate(p4, p3), p2), g1)), and_gate(and_gate(and_gate(and_gate(p4, p3), p2), p1), *c0));
// 准备计算一级的所有c值,下面这些是二级所有的c值
long c_2[4]={*c0,c16,c32,c48};
// 最终输出结果
long result = 0;
// 当前计算第几位
int r = 0;
for(int i=0;i<4;i++)
{
// 根据二级的c值计算一级的c值
long p4 =alu_bit(out_pm,i*4+3);
long p3 =alu_bit(out_pm,i*4+2);
long p2 =alu_bit(out_pm,i*4+1);
long p1 =alu_bit(out_pm,i*4+0);
long g4 =alu_bit(out_gm,i*4+3);
long g3 =alu_bit(out_gm,i*4+2);
long g2 =alu_bit(out_gm,i*4+1);
long g1 =alu_bit(out_gm,i*4+0);
long c1 = or_gate(g1, and_gate(p1, c_2[i]));
long c2 = or_gate(or_gate(g2, and_gate(p2, g1)),and_gate(and_gate(p2, p1), c_2[i]));
long c3 = or_gate(or_gate(or_gate(g3, and_gate(p3, g2)), and_gate(and_gate(p3, p2), g1)), and_gate(and_gate(and_gate(p3, p2), p1), c_2[i]));
// 这个没啥用,其实可以不用计算,但是其实电路中也没啥影响,毕竟都是并行的,都消耗2个门延迟
//long c4 = or_gate(or_gate(or_gate(or_gate(g4, and_gate(p4, g3)), and_gate(and_gate(p4, p3), g2)), and_gate(and_gate(and_gate(p4, p3), p2), g1)), and_gate(and_gate(and_gate(and_gate(p4, p3), p2), p1), c_2[i]));
// 根据1级的c值计算0级所有的c值
long c_1[4]={c_2[i],c1,c2,c3};
for(int j=0;j<4;j++)
{
long p4 =alu_bit(out_p,i*16+j*4+3);
long p3 =alu_bit(out_p,i*16+j*4+2);
long p2 =alu_bit(out_p,i*16+j*4+1);
long p1 =alu_bit(out_p,i*16+j*4+0);
long g4 =alu_bit(out_g,i*16+j*4+3);
long g3 =alu_bit(out_g,i*16+j*4+2);
long g2 =alu_bit(out_g,i*16+j*4+1);
long g1 =alu_bit(out_g,i*16+j*4+0);
long c1 = or_gate(g1, and_gate(p1, c_1[j]));
long c2 = or_gate(or_gate(g2, and_gate(p2, g1)),and_gate(and_gate(p2, p1), c_1[j]));
long c3 = or_gate(or_gate(or_gate(g3, and_gate(p3, g2)), and_gate(and_gate(p3, p2), g1)), and_gate(and_gate(and_gate(p3, p2), p1), c_1[j]));
//long c4 = or_gate(or_gate(or_gate(or_gate(g4, and_gate(p4, g3)), and_gate(and_gate(p4, p3), g2)), and_gate(and_gate(and_gate(p4, p3), p2), g1)), and_gate(and_gate(and_gate(and_gate(p4, p3), p2), p1), c_1[j]));
// 将c值写入result,result就相当于一个64位的电路
result |= c3<<(r+3);
result |= c2<<(r+2);
result |= c1<<(r+1);
result |= c_1[j]<<(r);
r+=4;
}
}
// 这里保存进位值
*c0 = c64;
// 两个异或操作获取位的计算值
return alu_xor(alu_xor(in_1, in_2,sizeof(long)*8), result,sizeof(long)*8);
}
int main(int argc, const char * argv[])
{
long c= 0;
long r0 = alu_add_bcla_64(-398, 283, 64, &c);
printf("r0 = %ld\n",r0);
long r1 = alu_add_bcla_64(398, 283, 64, &c);
printf("r1 = %ld\n",r1);
}
结果为:
r0 = -115
r1 = 681
总结
我们从不断优化的方案可以看出时间和空间的权衡方案,性能和速度的提升几乎必然伴随着电路的复杂度提高,需要更多的空间来安排电路的排线,需要更多的空间来放置更多的逻辑门。本篇文章完成时,荷兰的2纳米光刻机已经开始交付给intel。可预见的是,集成电路还会有大幅提升的空间。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!