Java 栈和队列的交互实现

---

队列和栈的区别

栈和队列都是常用的数据结构，它们的主要区别在于数据的插入和删除顺序。

栈 (Stack) 是一种后进先出 (Last-In-First-Out, LIFO) 的数据结构，只允许在一端进行插入和删除操作，这一端称为栈顶。新元素插入后成为新的栈顶，而删除时也只能删除栈顶元素。

队列 (Queue) 是一种先进先出 (First-In-First-Out, FIFO) 的数据结构，允许在两端进行插入和删除操作，插入在队尾，删除在队头。新元素插入时成为新的队尾，而删除时也只能删除队头元素。

一.用队列模拟实现栈

1.void push(int x) 将元素 x 压入栈顶。
2.int pop() 移除并返回栈顶元素。
3.int top() 返回栈顶元素。
4.boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

如上便是需要用队列来实现栈的四个基本操作。
我们试想，实现这些栈的操作，一个队列可以完成吗？
显然不可以，我们使用两个队列来实现栈的模拟

大体流程
1.入栈时：
如果两个都为空，那么想

1.1入栈

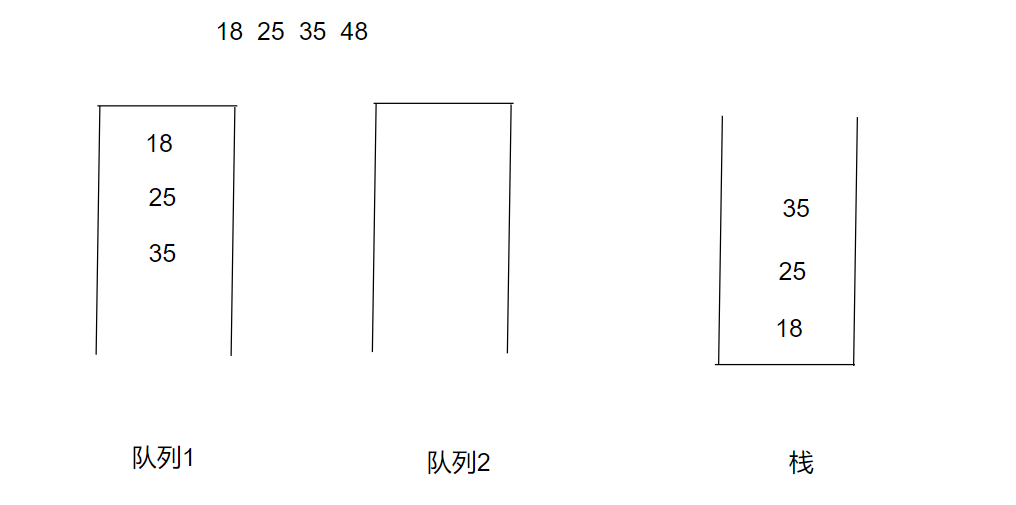
当我们要放入18 25 35 48 这一串数字入栈时，先放入18 25 35（放入时选择的队列是不为空的队列），模拟入队以及入栈时的状况，如下图

 public void push(int x) {
        if(empty()){
            queue1.offer(x);
            return;
        }
        if(!queue1.isEmpty()){
            queue1.offer(x);
        }else {
            queue2.offer(x);
        }
    }

1.2出栈

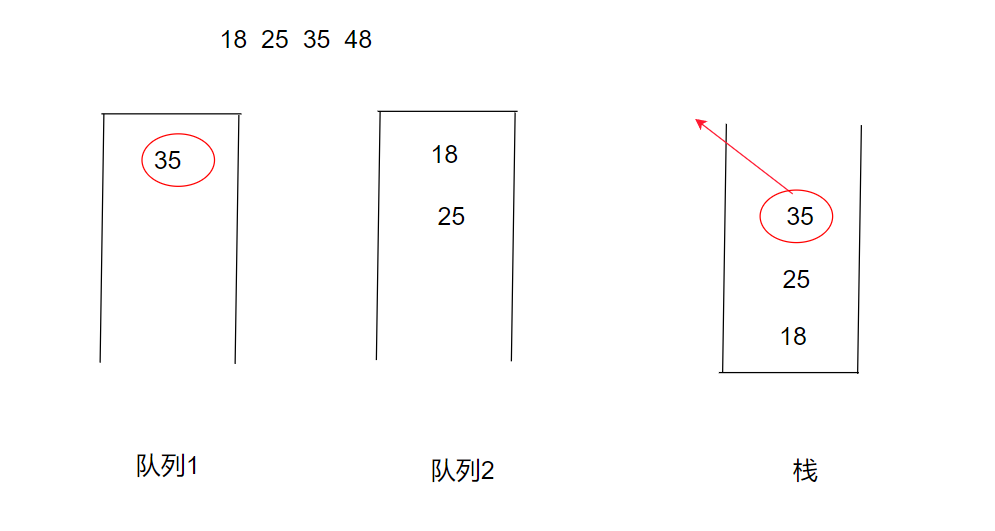
此时如果我们要将35出栈时，又该如何操作呢？此时我们就需要用到第二个队列，将队列一的前size－1个元素（也就是18 25)从队列一中出队，放入队列二中。此时队列一中的元素为35，队列二的元素为18 25 如下图。

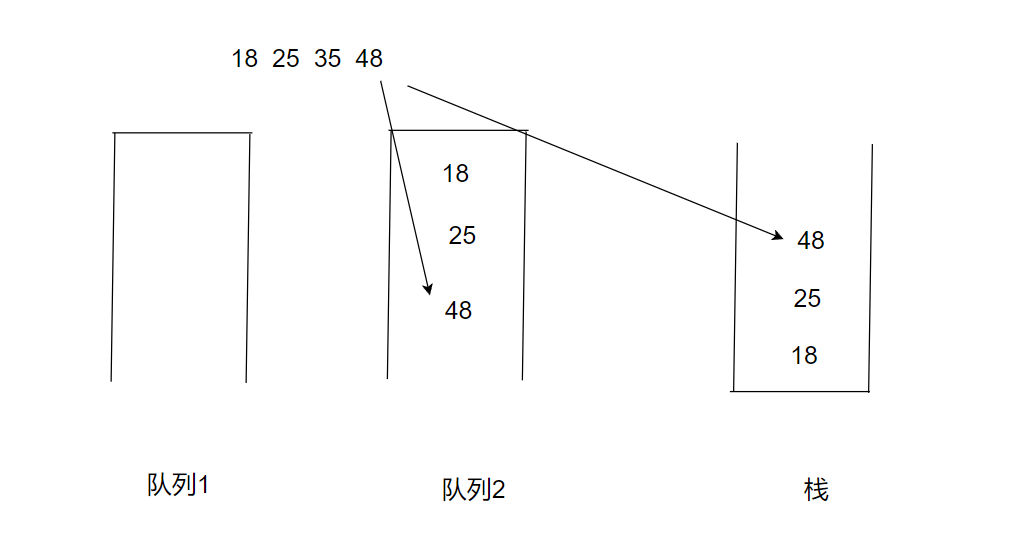
当初栈完成时，我们此时要将48入栈时，又该放入哪个栈中呢？我们考虑栈的特点（先入后出），我们将再入栈的元素放到不为空的队列中。

 public int pop() {
        if(empty()){
            return -1;
        }
        if(!queue1.isEmpty()){
            int size = queue1.size();
            for (int i = 0; i < size-1; i++) {
                queue2.offer(queue1.poll());
            }
            return queue1.poll();
        }else {
            int size = queue2.size();
            for (int i = 0; i < size-1; i++) {
                queue1.offer(queue2.poll());
            }
            return queue2.poll();
        }
    }

1.3返回栈顶元素

在实现pop的基础上，我们将声明一个变量temp来储存每次要移除的元素。

  public int top() {
        if(empty()){
            return -1;
        }
        if (!queue1.isEmpty()){
            int temp = -1;
            int size = queue1.size();
            for (int i = 0; i < size; i++) {
                temp = queue1.poll();
                queue2.offer(temp);
            }
            return temp;
        }else {
            int size = queue2.size();
            int temp = -1;
            for (int i = 0; i < size; i++) {
                temp = queue2.poll();
                queue1.offer(temp);
            }
            return temp;
        }
    }

1.4判断栈是否为空

当队列一和队列二都为空时，此时栈就为空。

public boolean empty() {
        return queue1.isEmpty()&&queue2.isEmpty();
    }

二.用栈模拟实现队列

我们也是用两个栈来模拟实现队列

2.1 入队

我们将所有入队的元素都放入栈一中，如下图

public void push(int x) {
          stack1.push(x);
    }

2.2出队

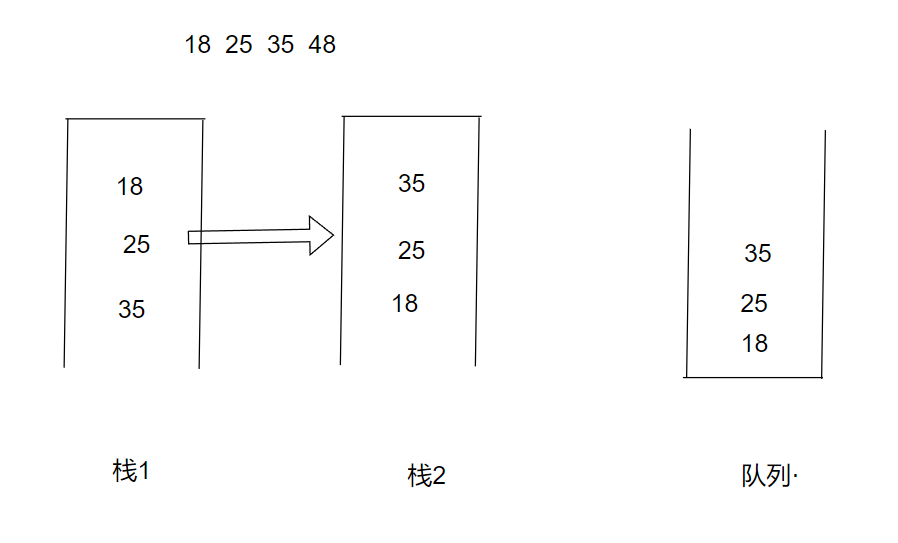
要出栈时，如果栈二不为空，就出栈二中的元素，如果栈二为空，将栈一中的所有元素一次性的全部push到栈二中，此时就将入栈的元素全部倒转过来了,(例如入栈时在栈中的入栈顺序依次排序为18 25 35，栈二中此时的元素入栈顺序是35 25 18，出栈时就先出18,就完成了转换）如下图

 public int pop() {
           if(empty()){
               return -1;
           }
           if (stack2.isEmpty()){
               while (!stack1.isEmpty()){
                   stack2.push(stack1.pop());
               }
           }
           return stack2.pop();
    }

2.3peek

peek只是将出队时的pop换成peek，就可以完成要求。

public int peek() {
        if(empty()){
            return -1;
        }
        if (stack2.isEmpty()){
            while (!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.peek();
    }

2.4判断队列是否为空

如果栈一和栈二都为空时，那么队列就为空。

 public boolean empty() {
          return stack1.isEmpty() && stack2.isEmpty();
    }

三.完整代码

3.1 队列模拟实现栈

class MyStack {

    Queue<Integer> queue1 ;
    Queue<Integer> queue2 ;
    public MyStack() {
         queue1 = new LinkedList<>();
         queue2 = new LinkedList<>();
    }
    public void push(int x) {
        if(empty()){
            queue1.offer(x);
            return;
        }
        if(!queue1.isEmpty()){
            queue1.offer(x);
        }else {
            queue2.offer(x);
        }
    }

    public int pop() {
        if(empty()){
            return -1;
        }
        if(!queue1.isEmpty()){
            int size = queue1.size();
            for (int i = 0; i < size-1; i++) {
                queue2.offer(queue1.poll());
            }
            return queue1.poll();
        }else {
            int size = queue2.size();
            for (int i = 0; i < size-1; i++) {
                queue1.offer(queue2.poll());
            }
            return queue2.poll();
        }
    }

    public int top() {
        if(empty()){
            return -1;
        }
        if (!queue1.isEmpty()){
            int temp = -1;
            int size = queue1.size();
            for (int i = 0; i < size; i++) {
                temp = queue1.poll();
                queue2.offer(temp);
            }
            return temp;
        }else {
            int size = queue2.size();
            int temp = -1;
            for (int i = 0; i < size; i++) {
                temp = queue2.poll();
                queue1.offer(temp);
            }
            return temp;
        }
    }

    public boolean empty() {
        return queue1.isEmpty()&&queue2.isEmpty();
    }
}

3.2栈模拟实现队列

class MyQueue {
    public Stack<Integer> stack1 ;
    public Stack<Integer> stack2;
    public MyQueue() {
     stack1 = new Stack<>();
     stack2 = new Stack<>();
    }

    public void push(int x) {
          stack1.push(x);
    }

    public int pop() {
           if(empty()){
               return -1;
           }
           if (stack2.isEmpty()){
               while (!stack1.isEmpty()){
                   stack2.push(stack1.pop());
               }
           }
           return stack2.pop();
    }

    public int peek() {
        if(empty()){
            return -1;
        }
        if (stack2.isEmpty()){
            while (!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.peek();
    }

    public boolean empty() {
          return stack1.isEmpty() && stack2.isEmpty();
    }
}