AcWing算法提高课-4.1.1格子游戏
算法提高课整理
CSDN个人主页:更好的阅读体验

原题链接
题目描述
Alice 和 Bob 玩了一个古老的游戏:首先画一个 n × n n \times n n×n 的点阵(下图 n = 3 n = 3 n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
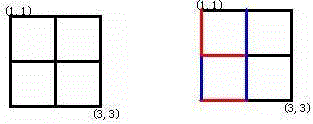
直到围成一个封闭的圈(面积不必为 1 1 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n n n 和 m m m。 n n n表示点阵的大小, m m m 表示一共画了 m m m 条线。
以后 m m m 行,每行首先有两个数字 ( x , y ) (x, y) (x,y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是 D D D,则是向下连一条边,如果是 R R R 就是向右连一条边。
输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如
m
m
m 步之后也没有结束,则输出一行 draw。
数据范围
1
≤
n
≤
200
1 \le n \le 200
1≤n≤200,
1
≤
m
≤
24000
1 \le m \le 24000
1≤m≤24000
输入样例:
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
输出样例:
4
思路
要判断是否成环。注意到如果最终成环,那么最后一次连接的时候两个端点在同一个连通块内。
对于连通块的问题,我们使用并查集解决。
问题解答
- Q:二维的网格如何放到并查集中?
- A:一种 trick,对于每个点 ( x , y ) (x,y) (x,y) 建立映射 f ( x , y ) = x × n + y f(x,y)=x\times n+y f(x,y)=x×n+y 即可。这样就建立了一个 0 ~ n × n ? 1 0 \sim n \times n - 1 0~n×n?1 的映射关系。
算法时间复杂度
m m m 轮操作,并查集均摊复杂度 O ( α ) O(\alpha) O(α),因此这一步 O ( α m ) O(\alpha m) O(αm)。
不过考虑到并查集的初始化复杂度为 O ( n 2 ) O(n^2) O(n2),因此预处理是瓶颈。
总复杂度 O ( n 2 ) O(n^2) O(n2)。
AC Code
C + + \text{C}++ C++
#include <iostream>
using namespace std;
const int N = 210;
int n, m;
int p[N * N];
int get(int x, int y)
{
return x * n + y;
}
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n * n; i ++ )
p[i] = i;
char op;
int x, y, r1, r2;
for (int i = 1; i <= m; i ++ )
{
cin >> x >> y >> op;
x -- , y -- ;
int r1 = get(x, y);
if (op == 'D') r2 = get(x + 1, y);
else r2 = get(x, y + 1);
r1 = find(r1), r2 = find(r2);
if (r1 == r2)
{
printf("%d\n", i);
exit(0);
}
p[r1] = r2;
}
puts("draw");
return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!