用微元思想求解三重积分——基于Matlab
2023-12-15 14:56:37
仅作自己学习使用
1. 题目
求解下列三重积分,其中A,μ,r都是常数。

求解的准确性可以用下式进行评估:
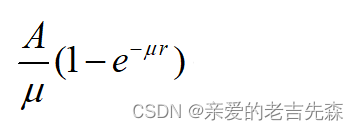
听过考研数一张宇课程的朋友应该指导,求解三重积分就是就一个面包,我们将面包无限细分为一个小块,我在代码中是将其细分为一个立方体,这样方便计算,通过设置不同的划分长度,可以获得不同的精度,但是随着划分区间的减少,计算量也会成倍增加。
2. Matlab实现代码
clc
clear
A = 10; % 源强密度
miu = 0.15;
m = 10; % 布点数
r = linspace(0,200,m);
dr = r(2)-r(1);
theta = linspace(0,2*pi,m);
dtheta = theta(2)-theta(1);
fia = linspace(0,pi,m);
dfia = fia(2)-fia(1);
fx = 0;
for i = 1 : length(r)
rr = r(i);
suma = 0;
for j = 1:length(fia)
sumb = 0;
jj = fia(j);
for k = 1:length(theta)
sumb = sumb + (A/(4*pi))*exp(-miu*rr)*sin(jj)*dtheta;
end
suma = suma + sumb*dfia;
end
fx = fx + suma*dr;
end
fx % 解析解
real = (A/miu)*(1-exp(-miu*max(r))) % 数值解
注意代码中的r,theta,fia我是直接通过linspace函数将其划分为了(m-1)个小的区间,计算的时候通过索引即可求解。其实代码中最重要的还是那三个for循环,如果不好想象的话可以从外到里逐步填空,具体思路如下:
step1:
%% step 1
fx = 0;
for i = 1:length(r)
rr = rr(i);
suma = 0; % 第二个for整体的微元
for j = 1:length(fia)
%% 填空
end
fx = fx + suma * dr; % 注意这一步df = fx * dx ,这是微元法的精髓
end
step2: 开始填空,这里就相当于是一个二重积分了,把里边的循环补充完整,就假设有无数个循环,里边个循环的写法和外边个循环的写法一样,直接模仿填空即可
fx = 0;
for i = 1:length(r)
rr = rr(i);
suma = 0; % 第二个for整体的微元
for j = 1:length(fia)
jj = fia(j);
sumb = 0;
for k = 1:length(theta)
%% 填空
end
suma = suma + sumb*dfia;
end
fx = fx + suma * dr; % 注意这一步df = fx * dx ,这是微元法的精髓
end
step3: 继续填空,里边个循环最简单了,现在就只是一个简单的积分了,注意里边的积分变量是theta,所以把其他都当作是常数来看待
fx = 0;
for i = 1:length(r)
rr = rr(i);
suma = 0; % 第二个for整体的微元
for j = 1:length(fia)
jj = fia(j);
sumb = 0;
for k = 1:length(theta)
sumb = sumb + (A/(4*pi))*exp(-miu*rr)*sin(jj)*dtheta;
end
suma = suma + sumb*dfia;
end
fx = fx + suma * dr; % 注意这一步df = fx * dx ,这是微元法的精髓
end
3. 结果
| m(区间个数-1) | fx(解析解) | real(数值解) |
|---|---|---|
| 100 | 78.0511 | 66.6667 |
| 300 | 70.3008 | 66.6667 |
| 600 | 68.4640 | 66.6667 |
| 1000 | 67.7404 | 66.6667 |
4. 问题
我是总感觉代码还有一点bug,也就是这行代码:
sumb = sumb + (A/(4*pi))*exp(-miu*rr)*sin(jj)*dtheta;
可能首末点的取值不正确,还请有知道的朋友多多批评指教!
文章来源:https://blog.csdn.net/qq_48515185/article/details/134937417
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!