【人工智能】实验三 A*算法求解八/十五数码问题实验与基础知识
实验三 A*算法求解八数码问题实验
实验目的
熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利用A*算法求解N数码难题,理解求解流程和搜索顺序。
实验内容
- 以8数码问题和15数码问题为例实现A*算法的求解程序(编程语言不限)。
- 设计两种不同的估价函数。
实验要求
- 设置相同的初始状态和目标状态,针对不同的估价函数,求得问题的解,比较它们对搜索算法性能的影响,包括扩展节点数、生成节点数等,填入表1。
表1:不同启发函数h(n)求解8数码问题的结果比较

- 设置与上述1相同的初始状态和目标状态,用宽度优先搜索算法(即令估计代价h(n)=0的A*算法)求得问题的解,以及搜索过程中的扩展节点数、生成节点数,填入表1。
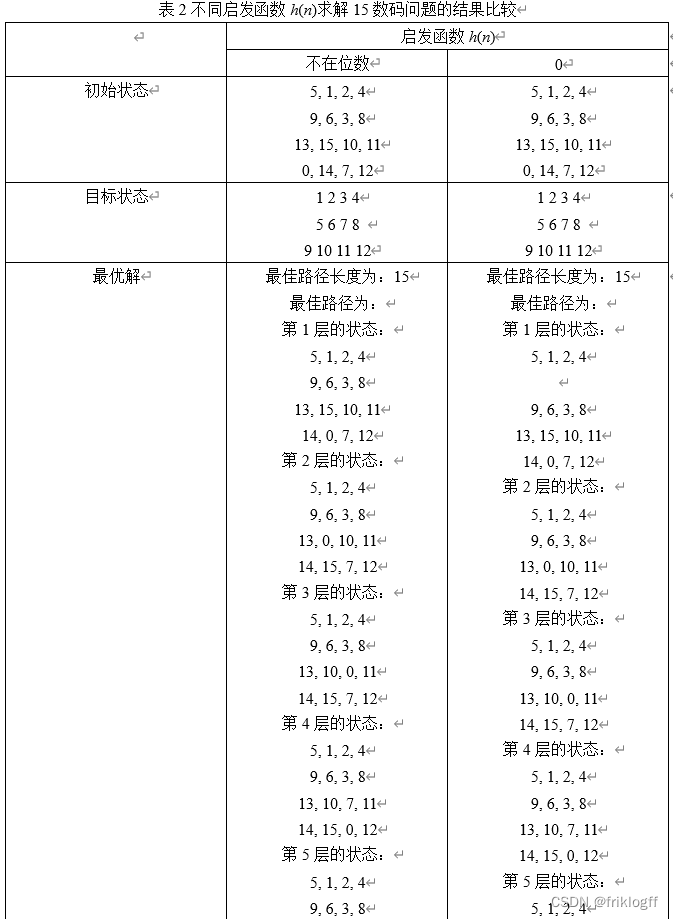
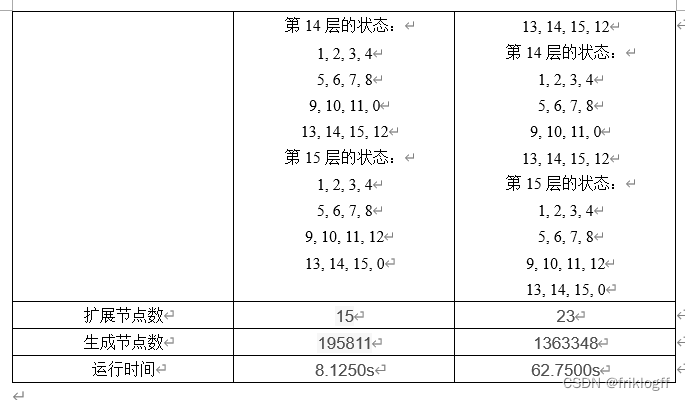
- 实现A*算法求解15数码问题的程序,设计两种不同的估价函数,然后重复上述2和3的实验内容, 把结果填入表2。
?
?
实验报告要求
- 分析不同的估价函数对A*算法性能的影响。
A算法是一种常用的启发式搜索算法,它通过综合考虑到达目标状态的代价和启发函数的估计来选择下一个扩展的节点。估价函数在A算法中起到关键作用,它用于评估当前节点到目标状态的代价。
不同的估价函数会对A*算法的性能产生影响,下面列举了几个常见的估价函数及其影响:
曼哈顿距离(Manhattan Distance):曼哈顿距离是指两点之间沿着坐标轴的距离总和,被广泛应用于求解拼图问题等。当估价函数选择曼哈顿距离时,A*算法会更倾向于优先扩展距离目标状态更近的节点。这种估价函数比较简单,但可能导致路径偏向直线而忽略其他因素。
欧几里得距离(Euclidean Distance):欧几里得距离是指两点之间的直线距离,它具有更好的几何意义。当估价函数选择欧几里得距离时,A*算法可能会探索更多的路径,并更倾向于选择直线路径。但欧几里得距离在某些情况下可能会高估代价,导致搜索效率较低。
启发式函数的加权和:有时候,一个估价函数难以完整地表达问题的复杂性。在这种情况下,可以考虑使用多个启发式函数,并为它们分配不同的权重。通过调整权重,可以平衡不同启发式函数之间的影响,提高A*算法的性能。
最小生成树估价函数(Minimum Spanning Tree Heuristic):这是一种基于图论中最小生成树概念的估价函数。它通过计算当前节点到剩余未拓展节点的最小生成树代价来评估节点的优先级。该估价函数具有更好的理论保证,并且在某些问题上性能良好。
总体而言,选择合适的估价函数对于A*算法的性能至关重要。一个好的估价函数应该能够准确估计代价,并且在搜索空间中引导算法朝着目标状态前进。对于特定问题,需要根据问题的特点和启发性信息设计合适的估价函数,以获得更好的性能。
- 根据宽度优先搜索算法和A*算法求解8、15数码问题的结果, 分析启发式搜索的特点。
宽度优先搜索算法:宽度优先搜索算法是一种无信息搜索算法,它从初始状态开始逐层扩展节点,直到找到目标状态为止。在8或15数码问题中,宽度优先搜索算法会逐渐扩展各个可能的状态,直到找到最短路径。它可以保证找到最短路径,但对于搜索空间较大的问题,宽度优先搜索的时间和空间复杂度都很高。
A*算法:A算法是一种启发式搜索算法,在估价函数的引导下选择下一个扩展节点。对于8或15数码问题,A算法使用曼哈顿距离作为估价函数
-
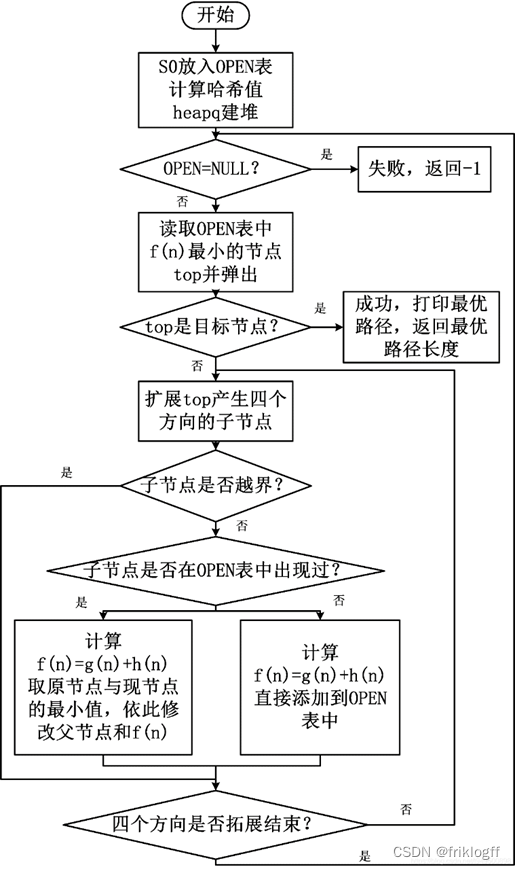
画出A*算法求解N数码问题的流程图。
-
提交源程序。
八位:
#include "iostream"
#include "stdlib.h"
#include "conio.h"
#include <math.h>
#include <windows.h>
#define size 3
using namespace std;
//定义二维数组来存储数据表示某一个特定状态
typedef int status[size][size];
struct SpringLink;
//定义状态图中的结点数据结构
typedef struct Node
{
status data;//结点所存储的状态 ,一个3*3矩阵
struct Node *parent;//指向结点的父亲结点
struct SpringLink *child;//指向结点的后继结点
struct Node *next;//指向open或者closed表中的后一个结点
int fvalue;//结点的总的路径
int gvalue;//结点的实际路径
int hvalue;//结点的到达目标的困难程度
}NNode , *PNode;
//定义存储指向结点后继结点的指针的地址
typedef struct SpringLink
{
struct Node *pointData;//指向结点的指针
struct SpringLink *next;//指向兄第结点
}SPLink , *PSPLink;
PNode open;
PNode closed;
//OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点
//开始状态与目标状态
/*
status startt = {1,3,0,8,2,4,7,6,5};最佳路径为2
status startt = {1,3,0,2,8,4,7,6,5};迭代超过20000次,手动停止
status startt = {2,8,3,1,6,4,7,0,5};
status startt = {2,8,3,6,0,4,1,7,5}; //实验报告
*/
int t=0; //迭代次数,相当于运行时间
int count_extendnode=0;//扩展结点
int count_sumnode=0; //生成节点
status startt = {2,8,3,6,0,4,1,7,5}; //实验报告
status target = {1,2,3,8,0,4,7,6,5};
//初始化一个空链表
void initLink(PNode &Head)
{
Head = (PNode)malloc(sizeof(NNode));
Head->next = NULL;
}
//判断链表是否为空
bool isEmpty(PNode Head)
{
if(Head->next == NULL)
return true;
else
return false;
}
//从链表中拿出一个数据
void popNode(PNode &Head , PNode &FNode)
{
if(isEmpty(Head))
{
FNode = NULL;
return;
}
FNode = Head->next;
Head->next = Head->next->next;
FNode->next = NULL;
}
//向结点的最终后继结点链表中添加新的子结点
void addSpringNode(PNode &Head , PNode newData)
{
PSPLink newNode = (PSPLink)malloc(sizeof(SPLink));
newNode->pointData = newData;
newNode->next = Head->child;
Head->child = newNode;
}
//释放状态图中存放结点后继结点地址的空间
void freeSpringLink(PSPLink &Head)
{
PSPLink tmm;
while(Head != NULL)
{
tmm = Head;
Head = Head->next;
free(tmm);
}
}
//释放open表与closed表中的资源
void freeLink(PNode &Head)
{
PNode tmn;
tmn = Head;
Head = Head->next;
free(tmn);
while(Head != NULL)
{
//首先释放存放结点后继结点地址的空间
freeSpringLink(Head->child);
tmn = Head;
Head = Head->next;
free(tmn);
}
}
//向普通链表中添加一个结点
void addNode(PNode &Head , PNode &newNode)
{
newNode->next = Head->next;
Head->next = newNode;
}
//向非递减排列的链表中添加一个结点(已经按照权值进行排序)
void addAscNode(PNode &Head , PNode &newNode)
{
PNode P;
PNode Q;
P = Head->next;
Q = Head;
while(P != NULL && P->fvalue < newNode->fvalue)
{
Q = P;
P = P->next;
}
//上面判断好位置之后,下面就是简单的插入了
newNode->next = Q->next;
Q->next = newNode;
}
/*
//计算结点的 h 值 f=g+h. 按照不在位的个数进行计算
int computeHValue(PNode theNode)
{
int num = 0;
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
if(theNode->data[i][j] != target[i][j])
num++;
}
}
return num;
}
//计算结点的 h 值 f=g+h. 按照将牌不在位的距离和进行计算
int computeHValue(PNode theNode)
{
int num = 0;
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
if(theNode->data[i][j] != target[i][j]&&theNode->data[i][j] !=0){
for(int ii=0;ii<3;ii++){
for(int jj=0;jj<3;jj++){
if(theNode->data[i][j] == target[ii][jj]){
num+=abs(ii-i)+abs(jj-j);
break;
}
}
}
}
}
}
return num;
} */
//计算结点的f,g,h值
void computeAllValue(PNode &theNode , PNode parentNode)
{
if(parentNode == NULL)
theNode->gvalue = 0;
else
theNode->gvalue = parentNode->gvalue + 1;
// theNode->hvalue = computeHValue(theNode);
theNode->hvalue = 0;
theNode->fvalue = theNode->gvalue + theNode->hvalue;
}
//初始化函数,进行算法初始条件的设置
void initial()
{
//初始化open以及closed表
initLink(open);
initLink(closed);
//初始化起始结点,令初始结点的父节点为空结点
PNode NULLNode = NULL;
PNode Start = (PNode)malloc(sizeof(NNode));
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
Start->data[i][j] = startt[i][j];
}
}
Start->parent = NULL;
Start->child = NULL;
Start->next = NULL;
computeAllValue(Start , NULLNode);
//起始结点进入open表
addAscNode(open , Start);
}
//将B节点的状态赋值给A结点
void statusAEB(PNode &ANode , PNode BNode)
{
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
ANode->data[i][j] = BNode->data[i][j];
}
}
}
//两个结点是否有相同的状态
bool hasSameStatus(PNode ANode , PNode BNode)
{
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
if(ANode->data[i][j] != BNode->data[i][j])
return false;
}
}
return true;
}
//结点与其祖先结点是否有相同的状态
bool hasAnceSameStatus(PNode OrigiNode , PNode AnceNode)
{
while(AnceNode != NULL)
{
if(hasSameStatus(OrigiNode , AnceNode))
return true;
AnceNode = AnceNode->parent;
}
return false;
}
//取得方格中空的格子的位置
void getPosition(PNode theNode , int &row , int &col)
{
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
if(theNode->data[i][j] == 0)
{
row = i;
col = j;
return;
}
}
}
}
//交换两个数字的值
void changeAB(int &A , int &B)
{
int C;
C = B;
B = A;
A = C;
}
//检查相应的状态是否在某一个链表中
bool inLink(PNode spciNode , PNode theLink , PNode &theNodeLink , PNode &preNode)
{
preNode = theLink;
theLink = theLink->next;
while(theLink != NULL)
{
if(hasSameStatus(spciNode , theLink))
{
theNodeLink = theLink;
return true;
}
preNode = theLink;
theLink = theLink->next;
}
return false;
}
//产生结点的后继结点(与祖先状态不同)链表
void SpringLink(PNode theNode , PNode &spring)
{
int row;
int col;
getPosition(theNode , row , col);
//空的格子右边的格子向左移动
if(col != 2)
{
PNode rlNewNode = (PNode)malloc(sizeof(NNode));
statusAEB(rlNewNode , theNode);
changeAB(rlNewNode->data[row][col] , rlNewNode->data[row][col + 1]);
if(hasAnceSameStatus(rlNewNode , theNode->parent))
{
free(rlNewNode);//与父辈相同,丢弃本结点
}
else
{
rlNewNode->parent = theNode;
rlNewNode->child = NULL;
rlNewNode->next = NULL;
computeAllValue(rlNewNode , theNode);
//将本结点加入后继结点链表
addNode(spring , rlNewNode);
}
}
//空的格子左边的格子向右移动
if(col != 0)
{
PNode lrNewNode = (PNode)malloc(sizeof(NNode));
statusAEB(lrNewNode , theNode);
changeAB(lrNewNode->data[row][col] , lrNewNode->data[row][col - 1]);
if(hasAnceSameStatus(lrNewNode , theNode->parent))
{
free(lrNewNode);//与父辈相同,丢弃本结点
}
else
{
lrNewNode->parent = theNode;
lrNewNode->child = NULL;
lrNewNode->next = NULL;
computeAllValue(lrNewNode , theNode);
//将本结点加入后继结点链表
addNode(spring , lrNewNode);
}
}
//空的格子上边的格子向下移动
if(row != 0)
{
PNode udNewNode = (PNode)malloc(sizeof(NNode));
statusAEB(udNewNode , theNode);
changeAB(udNewNode->data[row][col] , udNewNode->data[row - 1][col]);
if(hasAnceSameStatus(udNewNode , theNode->parent))
{
free(udNewNode);//与父辈相同,丢弃本结点
}
else
{
udNewNode->parent = theNode;
udNewNode->child = NULL;
udNewNode->next = NULL;
computeAllValue(udNewNode , theNode);
//将本结点加入后继结点链表
addNode(spring , udNewNode);
}
}
//空的格子下边的格子向上移动
if(row != 2)
{
PNode duNewNode = (PNode)malloc(sizeof(NNode));
statusAEB(duNewNode , theNode);
changeAB(duNewNode->data[row][col] , duNewNode->data[row + 1][col]);
if(hasAnceSameStatus(duNewNode , theNode->parent))
{
free(duNewNode);//与父辈相同,丢弃本结点
}
else
{
duNewNode->parent = theNode;
duNewNode->child = NULL;
duNewNode->next = NULL;
computeAllValue(duNewNode , theNode);
//将本结点加入后继结点链表
addNode(spring , duNewNode);
}
}
}
//输出给定结点的状态
void outputStatus(PNode stat)
{
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
cout << stat->data[i][j] << " ";
}
cout << endl;
}
}
//输出最佳的路径
void outputBestRoad(PNode goal)
{
int deepnum = goal->gvalue;
if(goal->parent != NULL)
{
outputBestRoad(goal->parent);
}
cout << "第" << deepnum-- << "层的状态:" << endl;
outputStatus(goal);
}
void AStar()
{
PNode tmpNode;//指向从open表中拿出并放到closed表中的结点的指针
PNode spring;//tmpNode的后继结点链
PNode tmpLNode;//tmpNode的某一个后继结点
PNode tmpChartNode;
PNode thePreNode;//指向将要从closed表中移到open表中的结点的前一个结点的指针
bool getGoal = false;//标识是否达到目标状态
long numcount = 1;//记录从open表中拿出结点的序号
initial();//对函数进行初始化
initLink(spring);//对后继链表的初始化
tmpChartNode = NULL;
//Target.data=target;
cout<<"1"<<endl;
PNode Target = (PNode)malloc(sizeof(NNode));
for(int i = 0 ; i < 3 ; i++)
{
for(int j = 0 ; j < 3 ; j++)
{
Target->data[i][j] =target[i][j];
}
}
cout<<"1"<<endl;
cout << "从open表中拿出的结点的状态及相应的值" << endl;
while(!isEmpty(open))
{
t++;
//从open表中拿出f值最小的元素,并将拿出的元素放入closed表中
popNode(open , tmpNode);
addNode(closed , tmpNode);
count_extendnode=count_extendnode+1;
cout << "第" << numcount++ << "个状态是:" << endl;
outputStatus(tmpNode);
cout << "其f值为:" << tmpNode->fvalue << endl;
cout << "其g值为:" << tmpNode->gvalue << endl;
cout << "其h值为:" << tmpNode->hvalue << endl;
/* //如果拿出的元素是目标状态则跳出循环
if(computeHValue(tmpNode) == 0)
{ count_extendnode=count_extendnode-1;
getGoal = true;
break;
}*/
//如果拿出的元素是目标状态则跳出循环
if(hasSameStatus(tmpNode,Target)== true)
{ count_extendnode=count_extendnode-1;
getGoal = true;
break;
}
//产生当前检测结点的后继(与祖先不同)结点列表,产生的后继结点的parent属性指向当前检测的结点
SpringLink(tmpNode , spring);
//遍历检测结点的后继结点链表
while(!isEmpty(spring))
{
popNode(spring , tmpLNode);
//状态在open表中已经存在,thePreNode参数在这里并不起作用
if(inLink(tmpLNode , open , tmpChartNode , thePreNode))
{
addSpringNode(tmpNode , tmpChartNode);
if(tmpLNode->gvalue < tmpChartNode->gvalue)
{
tmpChartNode->parent = tmpLNode->parent;
tmpChartNode->gvalue = tmpLNode->gvalue;
tmpChartNode->fvalue = tmpLNode->fvalue;
}
free(tmpLNode);
}
//状态在closed表中已经存在
else if(inLink(tmpLNode , closed , tmpChartNode , thePreNode))
{
addSpringNode(tmpNode , tmpChartNode);
if(tmpLNode->gvalue < tmpChartNode->gvalue)
{
PNode commu;
tmpChartNode->parent = tmpLNode->parent;
tmpChartNode->gvalue = tmpLNode->gvalue;
tmpChartNode->fvalue = tmpLNode->fvalue;
freeSpringLink(tmpChartNode->child);
tmpChartNode->child = NULL;
popNode(thePreNode , commu);
addAscNode(open , commu);
}
free(tmpLNode);
}
//新的状态即此状态既不在open表中也不在closed表中
else
{
addSpringNode(tmpNode , tmpLNode);
addAscNode(open , tmpLNode);
count_sumnode+=1;//生成节点
}
}
}
//目标可达的话,输出最佳的路径
if(getGoal)
{
cout << endl;
cout << "最佳路径长度为:" << tmpNode->gvalue << endl;
cout << "最佳路径为:" <<endl;
outputBestRoad(tmpNode);
}
//释放结点所占的内存
freeLink(open);
freeLink(closed);
// getch();
}
int main()
{ double start = GetTickCount();
AStar();
printf("生成节点数目:%d\n",count_sumnode);
printf("扩展节点数目:%d\n",count_extendnode);
printf("运行时间:%f\n",GetTickCount()-start);
return 0;
}
十五位:
#-*-coding:utf-8-*-
import heapq
import copy
import time
import math
import argparse
# 初始状态
# S0 = [[11, 9, 4, 15],
# [1, 3, 0, 12],
# [7, 5, 8, 6],
# [13, 2, 10, 14]]
S0 = [[5, 1, 2, 4],
[9, 6, 3, 8],
[13, 15, 10, 11],
[0, 14, 7, 12]]
# 目标状态
SG = [[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 0]]
# 上下左右四个方向移动
MOVE = {'up': [1, 0],
'down': [-1, 0],
'left': [0, -1],
'right': [0, 1]}
# OPEN表
OPEN = []
# 节点的总数
SUM_NODE_NUM = 0
# 状态节点
class State(object):
def __init__(self, deepth=0, rest_dis=0.0, state=None, hash_value=None, father_node=None):
'''
初始化
:参数 deepth: 从初始节点到目前节点所经过的步数
:参数 rest_dis: 启发距离
:参数 state: 节点存储的状态 4*4的列表
:参数 hash_value: 哈希值,用于判重
:参数 father_node: 父节点指针
'''
self.deepth = deepth
self.rest_dis = rest_dis
self.fn = self.deepth + self.rest_dis
self.child = [] # 孩子节点
self.father_node = father_node # 父节点
self.state = state # 局面状态
self.hash_value = hash_value # 哈希值
def __lt__(self, other): # 用于堆的比较,返回距离最小的
return self.fn < other.fn
def __eq__(self, other): # 相等的判断
return self.hash_value == other.hash_value
def __ne__(self, other): # 不等的判断
return not self.__eq__(other)
def cal_M_distence(cur_state):
'''
计算曼哈顿距离
:参数 state: 当前状态,4*4的列表, State.state
:返回: M_cost 每一个节点计算后的曼哈顿距离总和
'''
M_cost = 0
for i in range(4):
for j in range(4):
if cur_state[i][j] == SG[i][j]:
continue
num = cur_state[i][j]
if num == 0:
x, y = 3, 3
else:
x = num / 4 # 理论横坐标
y = num - 4 * x - 1 # 理论的纵坐标
M_cost += (abs(x - i) + abs(y - j))
return M_cost
def cal_E_distence(cur_state):
'''
计算曼哈顿距离
:参数 state: 当前状态,4*4的列表, State.state
:返回: M_cost 每一个节点计算后的曼哈顿距离总和
'''
E_cost = 0
for i in range(4):
for j in range(4):
if cur_state[i][j] == SG[i][j]:
continue
num = cur_state[i][j]
if num == 0:
x, y = 3, 3
else:
x = num / 4 # 理论横坐标
y = num - 4 * x - 1 # 理论的纵坐标
E_cost += math.sqrt((x - i)*(x - i) + (y - j)*(y - j))
return E_cost
def generate_child(sn_node, sg_node, hash_set, open_table, cal_distence):
'''
生成子节点函数
:参数 sn_node: 当前节点
:参数 sg_node: 最终状态节点
:参数 hash_set: 哈希表,用于判重
:参数 open_table: OPEN表
:参数 cal_distence: 距离函数
:返回: None
'''
if sn_node == sg_node:
heapq.heappush(open_table, sg_node)
print('已找到终止状态!')
return
for i in range(0, 4):
for j in range(0, 4):
if sn_node.state[i][j] != 0:
continue
for d in ['up', 'down', 'left', 'right']: # 四个偏移方向
x = i + MOVE[d][0]
y = j + MOVE[d][1]
if x < 0 or x >= 4 or y < 0 or y >= 4: # 越界了
continue
state = copy.deepcopy(sn_node.state) # 复制父节点的状态
state[i][j], state[x][y] = state[x][y], state[i][j] # 交换位置
h = hash(str(state)) # 哈希时要先转换成字符串
if h in hash_set: # 重复了
continue
hash_set.add(h) # 加入哈希表
# 记录扩展节点的个数
global SUM_NODE_NUM
SUM_NODE_NUM += 1
deepth = sn_node.deepth + 1 # 已经走的距离函数
rest_dis = cal_distence(state) # 启发的距离函数
node = State(deepth, rest_dis, state, h, sn_node) # 新建节点
sn_node.child.append(node) # 加入到孩子队列
heapq.heappush(open_table, node) # 加入到堆中
# show_block(state, deepth) # 打印每一步的搜索过程
def show_block(block, step):
print("------", step, "--------")
for b in block:
print(b)
def print_path(node):
'''
输出路径
:参数 node: 最终的节点
:返回: None
'''
print("最终搜索路径为:")
steps = node.deepth
stack = [] # 模拟栈
while node.father_node is not None:
stack.append(node.state)
node = node.father_node
stack.append(node.state)
step = 0
while len(stack) != 0:
t = stack.pop()
show_block(t, step)
step += 1
return steps
def A_start(start, end, distance_fn, generate_child_fn):
'''
A*算法
:参数 start: 起始状态
:参数 end: 终止状态
:参数 distance_fn: 距离函数,可以使用自定义的
:参数 generate_child_fn: 产生孩子节点的函数
:返回: 最优路径长度
'''
root = State(0, 0, start, hash(str(S0)), None) # 根节点
end_state = State(0, 0, end, hash(str(SG)), None) # 最后的节点
if root == end_state:
print("start == end !")
OPEN.append(root)
heapq.heapify(OPEN)
node_hash_set = set() # 存储节点的哈希值
node_hash_set.add(root.hash_value)
while len(OPEN) != 0:
top = heapq.heappop(OPEN)
if top == end_state: # 结束后直接输出路径
return print_path(top)
# 产生孩子节点,孩子节点加入OPEN表
generate_child_fn(sn_node=top, sg_node=end_state, hash_set=node_hash_set,
open_table=OPEN, cal_distence=distance_fn)
print("无搜索路径!") # 没有路径
return -1
if __name__ == '__main__':
# 可配置式运行文件
parser = argparse.ArgumentParser(description='选择距离计算方法')
parser.add_argument('--method', '-m', help='method 选择距离计算方法(cal_E_distence or cal_M_distence)', default = 'cal_M_distence')
args = parser.parse_args()
method = args.method
time1 = time.time()
if method == 'cal_E_distence':
length = A_start(S0, SG, cal_E_distence, generate_child)
else:
length = A_start(S0, SG, cal_M_distence, generate_child)
time2 = time.time()
if length != -1:
if method == 'cal_E_distence':
print("采用欧式距离计算启发函数")
else:
print("采用曼哈顿距离计算启发函数")
print("搜索最优路径长度为", length)
print("搜索时长为", (time2 - time1), "s")
print("共检测节点数为", SUM_NODE_NUM)
}
- 不同估价函数对A*算法性能的影响分析:
? 针对不同的估价函数,比较其在搜索过程中的扩展节点数、生成节点数以及运行时间。分析估价函数对算法性能的影响。 - 宽度优先搜索和A算法求解数码问题的比较分析:
? 比较宽度优先搜索和A算法在求解8数码问题时的扩展节点数、生成节点数等性能指标,分析启发式搜索的特点。 - A算法求解N数码问题的流程图:
? 画出A算法求解N数码问题的流程图,明确每个步骤和决策点,以展示算法的搜索流程。 - 提交源程序:
? 提交实现A*算法的源代码,包括估价函数的设计和算法实现部分。
实验思考及实践
估价函数选择:
在设计估价函数时,需要权衡精度和计算复杂度。一些常见的估价函数包括曼哈顿距离、不在位数等。曼哈顿距离计算复杂度较高,但更准确,而不在位数计算简单但可能不够精确。在实验中,对于不同问题和数据集,可以根据实际情况选择合适的估价函数。
A算法性能分析:
A算法在搜索过程中利用估价函数进行启发式搜索,能够更智能地选择节点进行扩展,相比于宽度优先搜索,减少了搜索空间,提高了搜索效率。然而,不同的估价函数会导致算法性能的差异,有时需要根据具体问题进行调优。
流程图绘制:
画出A算法求解N数码问题的流程图有助于理解算法的执行过程,包括节点扩展、估价值计算、优先队列的维护等关键步骤。流程图能够直观地展示算法的执行逻辑,便于深入理解和讨论。
实验总结
通过本次实验,我深入学习了启发式搜索和A算法的基本原理,并通过具体问题的求解实践,加深了对算法性能和估价函数选择的理解。实验过程中,对搜索算法的性能指标进行比较分析,能够更好地评估算法的优劣。这次实验对我的深度学习和掌握算法设计的能力都有很好的提升。
当然,我来为你提供更具体的内容:
图遍历算法
广度优先搜索(BFS)
广度优先搜索是一种图遍历算法,它从起始节点开始,逐层地向外扩展,确保先访问距离起始节点更近的节点。具体步骤如下:
- 将起始节点放入队列。
- 从队列中取出一个节点,将其标记为已访问。
- 将该节点的未访问邻居节点加入队列。
- 重复步骤2和3,直到队列为空。
深度优先搜索(DFS)
深度优先搜索是一种图遍历算法,它从起始节点开始,沿着路径尽可能深入搜索,直到无法再深入为止,然后回退到上一个节点继续搜索。具体步骤如下:
- 将起始节点放入栈。
- 从栈中取出一个节点,将其标记为已访问。
- 将该节点的未访问邻居节点加入栈。
- 重复步骤2和3,直到栈为空。
优先队列
优先队列的基本概念
优先队列是一种特殊的队列,其中每个元素都有一个与之关联的优先级。在优先队列中,元素按照优先级进行排序,优先级高的元素先出队列。
优先队列的实现方式
常见的实现优先队列的方式有二叉堆、斐波那契堆等。其中,二叉堆是一种完全二叉树,可以用数组实现,它满足堆的性质,即父节点的优先级大于或等于子节点的优先级。
如何根据估价函数的评估结果选择合适的节点进行扩展
在启发式搜索中,根据估价函数的评估结果选择合适的节点进行扩展是关键。一般情况下,优先选择具有较低估计代价的节点进行扩展,以期望更快地接近目标节点。因此,在优先队列中,节点的优先级应该基于估价函数的评估结果确定。
估价函数的设计
估价函数的作用和目标
估价函数用于评估当前节点到目标节点的估计代价。它的作用是指导搜索算法选择扩展的节点,并为算法提供启发性信息,以期望更快地找到解决方案。估价函数的目标是提供一个合理的代价评估,使算法能够在搜索过程中朝着最有希望的方向前进。
启发式规则和经验知识的运用
设计估价函数常常依赖于具体问题领域的启发式规则和经验知识。通过分析问题特征和相关规律,可以制定一些启发式规则,从而提供有益的评估信息。这些规则可以基于问题的结构、先验知识、可行解的特征等方面。
如何设计合理的估价函数以指导搜索方向和搜索顺序
设计合理的估价函数需要考虑多个因素,如问题的特性、可行解的特点以及算法的要求等。合理的估价函数应该能够准确地估计节点到目标节点的代价,同时能够提供有用的启发信息,以便算法能够优先选择最有希望的节点进行扩展。以下是设计合理的估价函数的一些常见方法:
-
直线距离估价:对于问题的状态空间,可以使用两点之间的直线距离作为估价函数的值。这适用于问题中有明确的空间关系,并且直线路径是最优路径的情况。
-
曼哈顿距离估价:对于网格型问题,可以使用曼哈顿距离作为估价函数的值。曼哈顿距离是两点横向和纵向距离的总和,适用于只能沿着格子移动的情况。
-
启发式规则估价:对于特定问题,可以基于问题的启发式规则和经验知识设计估价函数。这些启发式规则可以基于问题的特征、约束条件、可行解的特点等。通过分析问题的特点,设计合理的启发式规则可以提供更准确的估价函数。
启发式搜索算法的求解流程
启发式搜索算法的求解流程如下:
- 初始化搜索状态和起始节点。
- 创建一个优先队列,并将起始节点加入队列。
- 重复以下步骤直到找到目标节点或搜索队列为空:
- 从优先队列中取出优先级最高的节点。
- 如果该节点是目标节点,搜索完成,找到了解决方案。
- 根据估价函数评估节点的好坏,选择合适的节点加入优先队列。
- 如果搜索队列为空,表示未找到目标节点,搜索失败。
以上流程通过不断选择和扩展具有更高优先级的节点,指导搜索方向和搜索顺序,以期望更快地找到解决问题的路径。
综上所述,启发式搜索涉及图遍历算法、优先队列和估价函数的设计。理解和应用这些知识将有助于更好地使用启发式搜索算法来解决问题。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!