无约束优化问题求解(3):共轭梯度法
4. 共轭梯度法
4.1 共轭方向
最速下降法的线搜索采取精确线搜索时,由精确线搜索需要满足的条件:迭代点列 x k + 1 = x k + α k d k x_{k+1}=x_k+\alpha_kd_k xk+1?=xk?+αk?dk? , ? f ( x k + 1 ) T d k = 0 \nabla f(x_{k+1})^Td_k=0 ?f(xk+1?)Tdk?=0,其中 α k \alpha_{k} αk? 是第 k k k 次迭代的最优步长, d k d_{k} dk?是第 k k k 次迭代的负梯度方向 ? ? f ( x k ) -\nabla f(x_k) ??f(xk?),可以得到 ? f ( x k + 1 ) T ? f ( x k ) = ? ? f ( x k + 1 ) T d k / ∥ ? f ( x k ) ∥ 2 = 0. \begin{align}\nabla f(x_{k+1})^T\nabla f(x_k)=-\nabla f(x_{k+1})^Td_k/\|\nabla f(x_k)\|_2=0.\end{align} ?f(xk+1?)T?f(xk?)=??f(xk+1?)Tdk?/∥?f(xk?)∥2?=0.??
该式的含义即相邻两次的搜索方向是垂直的,如果我们考虑目标函数为二次多项式的形式,即
f
(
x
)
=
1
2
x
T
A
x
+
b
T
x
,
b
=
(
b
1
,
?
?
,
b
n
)
T
∈
R
n
,
\begin{align} f(x)=\dfrac{1}{2}x^TAx+b^Tx,\quad b=(b_1,\cdots,b_n)^T\in\mathbb{R}^n,\end{align}
f(x)=21?xTAx+bTx,b=(b1?,?,bn?)T∈Rn,??其中
A
:
=
d
i
a
g
(
λ
1
,
?
?
,
λ
n
)
A:=\mathbf{diag}(\lambda_1,\cdots,\lambda_n)
A:=diag(λ1?,?,λn?) 是一个对角矩阵,
λ
i
>
0
,
i
=
1
,
?
?
,
n
.
\lambda_i>0,\quad i=1,\cdots,n.
λi?>0,i=1,?,n. 此时,函数的等高面为一椭球(圆),基于精确线搜索的最速下降法的迭代点列以锯齿方向前进,如图 4.1的黑色实线所示,这使得其收敛速度变得缓慢.也就是说尽管最速下降法采用当前点梯度下降最快的方向作为搜索方向, 但该方向未必是较大范围内下降最快的方向,也就是说该方向不一定是较大范围内函数值幅度变化最大方向,而如果我们按照平行于坐标轴的方向进行精确搜索,如图 4.1左边的红色虚线所示, 在二维情形只需要两次就达到了最小值点,那么我们可以断言:对
n
n
n 维的二次函数优化问题(2),最多经过
n
n
n 次迭代就可以达到最小值点,上面的断言就是共轭方向法的想法.

对形如(2)的目标函数,由于 A : = d i a g ( λ 1 , ? ? , λ n ) , λ i > 0 , ? i = 1 , ? ? , n A:=\mathbf{diag}(\lambda_1,\cdots,\lambda_n),\lambda_i>0,\:i=1,\cdots,n A:=diag(λ1?,?,λn?),λi?>0,i=1,?,n. 我们有 f ( x ) = ∑ i = 1 n ( 1 2 λ i x i 2 + b i x i ) . f(x)=\sum_{i=1}^n\big(\frac12\lambda_ix_i^2+b_ix_i\big). f(x)=i=1∑n?(21?λi?xi2?+bi?xi?).也就是说对于每一个 i i i 而言,都是二次函数,根据二次函数的性质, 1 2 λ i x i 2 + b i x i \frac12\lambda_ix_i^2+b_ix_i 21?λi?xi2?+bi?xi? 在无约束的情况下必然可以取到最值, x = ( x 1 , ? ? , x n ) x=(x_1,\cdots,x_n) x=(x1?,?,xn?) 使得 f ( x ) f(x) f(x) 达到最小值当且仅当对 i = 1 , ? ? , n , x i i=1,\cdots,n,x_i i=1,?,n,xi? 使得 f i ( x i ) : = λ i x i 2 + b i x i f_i(x_i):=\lambda_ix_i^2+b_ix_i fi?(xi?):=λi?xi2?+bi?xi? 达到最小.
根据解析几何的知识,函数 f ( x ) f(x) f(x) 是二次曲面,且其等高面是一个椭球 (圆). 对 i = 1 , ? ? , n i= 1, \cdots , n i=1,?,n,记 e i e_i ei? 表示 R n \mathbb{R}^n Rn 中第 i i i个坐标向量. ? x 0 ∈ R n \forall x_0\in \mathbb{R} ^n ?x0?∈Rn,沿方向 d i = e i d_i=e_i di?=ei? 作精确搜索时,将搜索到 f i ( x i ) f_i(x_i) fi?(xi?) 的最小值点,而其余项不变,也就是说每次搜索只改变一个方向而保持其他方向不变,那么如此搜索最多 n n n 次后达到函数的最小值点,这也就是前面我们断言的内容.
但是这个时候可能又有疑问了,并不是所有的椭圆的轴都是和坐标轴平行的呀,那么如果这个时候还是以平行于坐标轴的方向来作为每次的搜索方向不一定会达到最快的效果呀。事实上确实如此,沿着坐标轴来搜索确实只是一种特殊的情况,如下图所示:

如图 4.2所示,当我们还以坐标轴的方向来作为搜索方向的时候,沿着等高线移动的时候并不是最快的.但是如果我们旋转一下坐标轴会发现,我们可以用适当的旋转角度,旋转坐标轴后,使得坐标轴和椭圆的轴平行,实际上由线性代数的知识我们可以知道,旋转坐标轴本质上是做了一种线性变换.
简单地说共轭方向其实就是线性变化后的坐标轴和椭圆的轴平行的方向.下面我们用线性代数的知识来推导一下这个过程.
一般地,若二次函数
f
(
x
)
=
1
2
x
T
A
x
+
b
T
x
\begin{align}f(x)=\frac12x^TAx+b^Tx\end{align}
f(x)=21?xTAx+bTx?? (3) 中
A
A
A 为
n
n
n 阶正定矩阵,但未必是对角矩阵,此时函数曲面的等高面仍是椭球,但主轴未必平行于坐标轴,如图 4.3(右) 所示. 这时,可以通过坐标变换将
A
A
A 对角化:取可逆矩阵
D
D
D,做坐标变换
x
=
D
y
x=Dy
x=Dy,记
c
=
D
T
b
c=D^Tb
c=DTb,则
f
(
x
)
=
1
2
y
T
(
D
T
A
D
)
y
+
c
T
y
.
f(x)=\frac12y^T(D^TAD)y+c^Ty.
f(x)=21?yT(DTAD)y+cTy.因此,当
D
T
A
D
D^TAD
DTAD 是一个对角矩阵时(并且对角线的元素均大于0),在
y
y
y 坐标系里沿坐标方向
e
i
,
?
i
=
1
,
?
?
,
n
e_i,~i=1,\cdots,n
ei?,?i=1,?,n, 做精确搜索,便可以在有限次内达到
f
(
x
)
f(x)
f(x) 的最小值点.
在
y
y
y 坐标系中的迭代
y
k
+
1
=
y
k
+
α
e
k
y_{k+1}=y_k+\alpha e_k
yk+1?=yk?+αek? ,根据坐标变换,等价于在原
x
x
x 坐标系中的迭代
x
k
+
1
=
x_{k+1}=
xk+1?=
x
k
+
α
D
e
k
,
?
k
=
0
,
1
,
.
.
.
,
n
?
1
x_k+\alpha De_k,\:k=0,1,...,n-1
xk?+αDek?,k=0,1,...,n?1.记
d
k
:
=
D
e
k
,
?
k
=
0
,
1
,
.
.
.
,
n
?
1
d_k:=De_k,\:k=0,1,...,n-1
dk?:=Dek?,k=0,1,...,n?1,那么
[
d
0
,
.
.
.
,
d
n
?
1
]
=
D
,
[d_0,...,d_{n-1}]=D,
[d0?,...,dn?1?]=D,即
d
0
,
.
.
.
,
d
n
?
1
d_0,...,d_{n-1}
d0?,...,dn?1? 是矩阵
D
D
D的列向量.此时,迭代公式为
x
k
+
1
=
x
k
+
α
d
k
x_k+ 1= x_k+ \alpha d_k
xk?+1=xk?+αdk?.这说明,只要我们在原坐标系中依次沿着
d
0
,
?
?
,
d
n
?
1
d_0,\cdots,d_{n-1}
d0?,?,dn?1?做精确搜索,便可在有限次达到
f
(
x
)
f(x)
f(x) 的最小值点
为此,我们需要先求得方向
d
0
,
d
1
,
?
?
,
d
n
?
1
d_0,d_1,\cdots,d_{n-1}
d0?,d1?,?,dn?1? 使得
D
T
A
D
D^TAD
DTAD 为对角矩阵.这等价于
d
i
T
A
d
j
=
0
,
i
,
j
=
0
,
1
,
?
?
,
n
?
1
;
?
i
≠
j
.
\begin{aligned}d_i^TAd_j=0,\quad i,j=0,1,\cdots,n-1;\:i\neq j.\end{aligned}
diT?Adj?=0,i,j=0,1,?,n?1;i=j.?由此,下面我们看看共轭方向的数学形式的定义。
定义 4.1 设
A
∈
R
n
×
n
A\in\mathbb{R}^{n\times n}
A∈Rn×n 是一个正定矩阵,非零向量
d
0
,
?
?
,
d
k
?
1
∈
R
n
d_0,\cdots,d_{k-1}\in\mathbb{R}^n
d0?,?,dk?1?∈Rn 称为是彼此
(
A
)
(A)
(A) 共轭的,如果它们满足
d
i
T
A
d
j
=
0
,
i
,
j
=
0
,
1
,
?
?
,
k
?
1
;
?
i
≠
j
.
\begin{aligned}d_i^TAd_j=0,\quad i,j=0,1,\cdots,k-1;\:i\neq j.\end{aligned}
diT?Adj?=0,i,j=0,1,?,k?1;i=j.?显然,向量
d
i
d_i
di? 与
d
j
d_j
dj? 共轭其实就是它们在内积
?
x
,
y
?
:
=
x
T
A
y
?x, y? := x^TAy
?x,y?:=xTAy 下为正交,由此两两 (A) 共轭的向量组是在上述内积意义下两两正交的向量组,所以必定线性无关.除此此外,如果
d
0
,
?
?
?
,
d
k
?
1
∈
R
n
d_0, ··· , d_k?1 ∈ \mathbb{R}^n
d0?,???,dk??1∈Rn 是彼此 (A) 共轭的,那么改变这些向量的符号仍然是彼此 (A) 共轭的.所以每一个
d
i
d_i
di? 未必是目标函数
f
(
x
)
f(x)
f(x) 下降的方向,这是因在沿着该方向进行搜索时需要同时考虑其反方向.
命题 4.1 设 A A A 是 n n n 阶正定矩阵, f f f 如(3) 所述, k ≥ 1 , d 0 , ? ? , d k ? 1 ∈ R n k\geq1,d_0,\cdots,d_{k-1}\in\mathbb{R}^n k≥1,d0?,?,dk?1?∈Rn 是一组是彼此 ( A ) (A) (A) 共轭的向量.任取 x 0 ∈ R n x_0\in\mathbb{R}^n x0?∈Rn,记 x j + 1 = x j + α j d j , j = 0 , 1 , ? ? , k ? 1 x_{j+1}=x_j+\alpha_jd_j, j=0,1,\cdots,k-1 xj+1?=xj?+αj?dj?,j=0,1,?,k?1,为精确搜索的点列 (由于不能保证 d j d_j dj? 为下降方向,故搜索时允许 α j \alpha_j αj? 为负数), 那么
( i ) ? ? f ( x k ) T d j = 0 , ? j = 0 , 1 , ? ? , k ? 1 ; (i)\:\nabla f(x_k)^Td_j=0,\:j=0,1,\cdots,k-1; (i)?f(xk?)Tdj?=0,j=0,1,?,k?1;
( i i ) ? x k = argmin ? x ∈ X k f ( x ) (ii)\:x_k=\operatorname{argmin}_{x\in X_k}f(x) (ii)xk?=argminx∈Xk??f(x),其中 X k : = x 0 + s p a n { d 0 , ? ? , d k ? 1 } ; X_k:=x_0+\mathbf{span}\{d_0,\cdots,d_{k-1}\}; Xk?:=x0?+span{d0?,?,dk?1?};
( i i i ) (iii) (iii) 当 k = n k=n k=n 时, x n x_n xn? 是 f f f在 R n \mathbb{R} ^n Rn 上的全局极小点.
首先不加证明,我们先看看这个命题说了个什么事情.由上述的命题我们可以看出? X k X_k Xk? 是?由向量组 { d 0 , ? ? , d k ? 1 } \{d_0,\cdots,d_{k-1}\} {d0?,?,dk?1?} 张成的线性空间。从上述命题我们可以简述一下共轭方向法的基本流程:从初始点 x 0 x_0 x0?开始,根据精确线搜索找到最优步长 α 0 \alpha_0 α0?,根据迭代式 x 1 = x 0 + α 0 d 0 , j = 0 , 1 , ? ? , k ? 1 x_{1}=x_0+\alpha_0d_0, j=0,1,\cdots,k-1 x1?=x0?+α0?d0?,j=0,1,?,k?1 以及条件 x 1 = argmin ? x ∈ X 1 f ( x ) x_1=\operatorname{argmin}_{x\in X_1}f(x) x1?=argminx∈X1??f(x),计算得到 x 1 x_1 x1?,其中 X 1 = x 0 + s p a n { d 0 } X_1 = x_0 + \mathbf{span}\{d_0\} X1?=x0?+span{d0?},这样就完成了一维的情况 R \mathbb{R} R .类似地从一维的情况 R \mathbb{R} R 逐步推广到 R n \mathbb{R}^n Rn,由于每一个“新添加”的维度都是与之前维度共轭的(这一性质由命题的条件给出,后续证明),所以自然线性无关,于是这样便能逐步地从初始点找到整个空间 R n \mathbf{R}^n Rn的共轭序列点.下面我们再看看命题是怎么样证明的.
证.
(
i
)
(i)
(i) 根据精确搜索条件,有
?
f
(
x
j
+
1
)
T
d
j
=
0
,
?
?
j
?
=
?
0
,
1
,
?
?
,
k
?
1.
\nabla f(x_{j+1})^Td_j=0,\:\forall j\:=\:0,1,\cdots,k-1.
?f(xj+1?)Tdj?=0,?j=0,1,?,k?1. 于是,
?
f
(
x
k
)
T
d
k
?
1
=
0
\nabla f(x_k)^Td_{k-1}=0
?f(xk?)Tdk?1?=0.而对于
j
=
0
,
1
,
?
?
,
k
?
2
j=0,1,\cdots,k-2
j=0,1,?,k?2,有
?
f
(
x
k
)
=
A
x
k
+
b
=
A
(
x
k
?
1
+
α
k
?
1
d
k
?
1
)
+
b
=
?
f
(
x
k
?
1
)
+
α
k
?
1
A
d
k
?
1
=
?
=
?
f
(
x
j
+
1
)
+
α
j
+
1
A
d
j
+
1
+
?
+
α
k
?
1
A
d
k
?
1
,
\begin{aligned} \nabla f(x_{k})& \begin{aligned}&=Ax_k+b=A(x_{k-1}+\alpha_{k-1}d_{k-1})+b=\nabla f(x_{k-1})+\alpha_{k-1}Ad_{k-1}\end{aligned} \\ &=\cdots \\ &=\nabla f(x_{j+1})+\alpha_{j+1}Ad_{j+1}+\cdots+\alpha_{k-1}Ad_{k-1}, \end{aligned}
?f(xk?)??=Axk?+b=A(xk?1?+αk?1?dk?1?)+b=?f(xk?1?)+αk?1?Adk?1??=?=?f(xj+1?)+αj+1?Adj+1?+?+αk?1?Adk?1?,?上式两边取转置后再同时右乘
d
j
d_j
dj? ,利用
?
f
(
x
j
+
1
)
T
d
j
=
0
,
?
?
j
?
=
?
0
,
1
,
?
?
,
k
?
1.
\nabla f(x_{j+1})^Td_j=0,\:\forall j\:=\:0,1,\cdots,k-1.
?f(xj+1?)Tdj?=0,?j=0,1,?,k?1. 可以得到
?
f
(
x
k
)
T
d
j
=
?
f
(
x
j
+
1
)
T
d
j
=
0
\nabla f( x_k) ^Td_j= \nabla f( {x_{j+ 1}}) ^Td_j= 0
?f(xk?)Tdj?=?f(xj+1?)Tdj?=0,
(
i
)
(i)
(i) 得证.
下面证 ( i i ) (ii) (ii),首先对于 x k x_k xk?,将其写开可以得到 x k = x k ? 1 + α k ? 1 d k ? 1 = ? = x 0 + ∑ j = 0 k ? 1 α j d j ∈ X k x_{k}=x_{k-1}+\alpha_{k-1}d_{k-1}=\cdots=x_{0}+\sum_{j=0}^{k-1}\alpha_{j}d_{j}\in X_{k} xk?=xk?1?+αk?1?dk?1?=?=x0?+j=0∑k?1?αj?dj?∈Xk?
对任意的
x
=
x
0
+
∑
j
=
0
k
?
1
β
j
d
j
∈
X
k
x= x_{0}+\sum_{j=0}^{k-1}\beta_{j}d_{j}\in X_{k}
x=x0?+∑j=0k?1?βj?dj?∈Xk?,根据 Taylor 展开,由于目标函数式二次函数,因此可以利用 Taylor展开得到
f
(
x
)
=
f
(
x
k
)
+
?
f
(
x
k
)
T
(
x
?
x
k
)
+
1
2
(
x
?
x
k
)
T
A
(
x
?
x
k
)
≥
f
(
x
k
)
+
?
f
(
x
k
)
T
(
x
?
x
k
)
=
f
(
x
k
)
+
?
f
(
x
k
)
T
[
∑
j
=
0
k
?
1
(
β
j
?
α
k
)
d
j
]
=
f
(
x
k
)
.
\begin{aligned}f(x)&=f(x_k)+\nabla f(x_k)^T(x-x_k)+\frac{1}{2}(x-x_k)^TA(x-x_k) \\ &\geq f(x_k)+\nabla f(x_k)^T(x-x_k) \\ &=f(x_k)+\nabla f(x_k)^T\Big[\sum_{j=0}^{k-1}(\beta_j-\alpha_k)d_j\Big]=f(x_k). \\ \end{aligned}
f(x)?=f(xk?)+?f(xk?)T(x?xk?)+21?(x?xk?)TA(x?xk?)≥f(xk?)+?f(xk?)T(x?xk?)=f(xk?)+?f(xk?)T[j=0∑k?1?(βj??αk?)dj?]=f(xk?).?上式中的不等号利用了结论:若矩阵
A
A
A 正定矩阵,则对于任意
x
∈
R
n
x\in\mathbb{R}^n
x∈Rn,都有
x
T
A
x
>
0
x^TAx >0
xTAx>0;第二个等号将
x
?
x
k
x-x_k
x?xk?展开计算即得.
所以, x k x_k xk?是 f ( x ) f(x) f(x) 在 X k X_k Xk? 中的最小值点.
( i i i ) (iii) (iii) 当 k = n k= n k=n 时,因为 d 0 , ? ? , d n ? 1 d_0, \cdots , d_n- 1 d0?,?,dn??1 线性无关,所以 X n ? 1 = R n X_{n-1}=\mathbb{R}^n Xn?1?=Rn.从而 x n x_n xn? 是 f f f在 R n \mathbb{R} ^n Rn 上的全局极小点.
基于给定的共轭方向的搜索方法称为共轭方向法. 如何快速地构造共轭方向组
d
0
,
?
?
,
d
n
?
1
d_0,\cdots,d_{n-1}
d0?,?,dn?1? 是该方法的关键所在. 虽然通过对矩阵
A
A
A 的特征分解可以得到共轭方向, 但其计算量为
O
(
n
3
)
O(n^3)
O(n3).实际上,若
x
0
x_{0}
x0?取得好,我们只需要少数几次迭代即可达到函数的极小值点.那么接下来我们就要看看一种在迭代过程中即时生成
d
k
d_k
dk? 的方法,称为共轭梯度法.
4.2 共轭梯度法
共轭梯度法是一种在迭代过程中利用梯度向量来逐步生成共轭向量组的方法,对于
目标函数
f
(
x
)
=
1
2
x
T
A
x
+
b
T
x
f(x)=\frac12x^TAx+b^Tx
f(x)=21?xTAx+bTx ,共轭梯度法按如下算法来生成共轭向量组.
首先,取充分小的数 ? > 0 \epsilon>0 ?>0. 任取初始点 x 0 ∈ R n x_0\in\mathbb{R}^n x0?∈Rn,若不满足终止条件 ∥ ? f ( x 0 ) ∥ 2 < ? \|\nabla f(x_0)\|_2<\epsilon ∥?f(x0?)∥2?<?,令 d 0 : = ? ? f ( x 0 ) d_0:=-\nabla f(x_0) d0?:=??f(x0?),则 ? f ( x 0 ) T d 0 = ? ∥ ? f ( x 0 ) ∥ 2 2 < 0 \nabla f(x_0)^Td_0=-\|\nabla f(x_0)\|_2^2<0 ?f(x0?)Td0?=?∥?f(x0?)∥22?<0,因而可以通过精确搜索得到该次迭代的最优步长 α 0 > 0 \alpha_0>0 α0?>0,使得 x 1 = x 0 + α 0 d 0 x_1=x_0+\alpha_0d_0 x1?=x0?+α0?d0? 满足 ? f ( x 1 ) T d 0 = 0. \nabla f(x_1)^Td_0=0. ?f(x1?)Td0?=0.
一般地,如果已经构造出了彼此 (A) 共轭的向量组
d
0
,
?
?
,
d
k
?
1
d_0,\cdots,d_{k-1}
d0?,?,dk?1? 和通过精确搜索所得迭代点列
x
j
+
1
=
x
j
+
α
j
d
j
,
?
j
=
0
,
1
,
.
.
.
,
k
?
1
x_{j+1}=x_j+\alpha_jd_j,\:j=0,1,...,k-1
xj+1?=xj?+αj?dj?,j=0,1,...,k?1, 其中
α
j
>
0
,
?
f
(
x
j
)
T
d
j
<
0
,
j
=
0
,
1
,
.
.
.
,
k
?
1
\alpha_j>0,\quad\nabla f(x_j)^Td_j<0,\quad j=0,1,...,k-1
αj?>0,?f(xj?)Tdj?<0,j=0,1,...,k?1若
∥
?
f
(
x
k
)
∥
2
≥
?
,
\|\nabla f( x_k) \|_2\geq \epsilon,
∥?f(xk?)∥2?≥?,令
d
k
:
=
?
?
f
(
x
k
)
+
∑
i
=
0
k
?
1
β
i
d
i
\begin{align}d_k:=-\nabla f(x_k)+\sum_{i=0}^{k-1}\beta_id_i\end{align}
dk?:=??f(xk?)+i=0∑k?1?βi?di???,并希望选取合适的参数
β
0
,
.
.
.
,
β
k
?
1
\beta_0,...,\beta_{k-1}
β0?,...,βk?1? 使得
d
0
,
?
?
,
d
k
?
1
,
d
k
d_0,\cdots,d_{k-1},d_k
d0?,?,dk?1?,dk? 彼此 (A) 共轭.也就是说这个过程是利用已知的彼此 (A) 共轭的向量组
d
0
,
?
?
,
d
k
?
1
d_0,\cdots,d_{k-1}
d0?,?,dk?1?,通过待定系数法来求解合适的参数,最终得到一个
d
k
d_k
dk?,使得
d
k
d_k
dk?与 向量组
d
0
,
?
?
,
d
k
?
1
d_0,\cdots,d_{k-1}
d0?,?,dk?1?两两共轭.
下面看看待定系数应该怎么求解,
d
0
,
?
?
,
d
k
?
1
,
d
k
d_0,\cdots,d_{k-1},d_k
d0?,?,dk?1?,dk? 彼此 (A) 共轭当且仅当
d
k
T
A
d
j
=
0
,
?
j
=
0
,
1
,
?
?
,
k
?
1
d_k^TAd_j=0,~j=0,1,\cdots,k-1
dkT?Adj?=0,?j=0,1,?,k?1, 即
(
?
?
f
(
x
k
)
+
∑
i
=
0
k
?
1
β
i
d
i
)
T
A
d
j
=
0
,
j
=
0
,
1
,
?
?
,
k
?
1.
\Big(-\nabla f(x_k)+\sum_{i=0}^{k-1}\beta_id_i\Big)^TAd_j=0,\quad j=0,1,\cdots,k-1.
(??f(xk?)+i=0∑k?1?βi?di?)TAdj?=0,j=0,1,?,k?1.
t
?
0
t-0
t?0
由于
d
0
,
?
?
,
d
k
?
1
d_0,\cdots,d_{k-1}
d0?,?,dk?1?是彼此
(
A
)
(A)
(A) 共轭的,所以上式等价于
β
j
d
j
T
A
d
j
=
?
f
(
x
k
)
T
A
d
j
\beta_jd_j^TAd_j=\nabla f(x_k)^TAd_j
βj?djT?Adj?=?f(xk?)TAdj?,即
β
j
=
?
f
(
x
k
)
T
A
d
j
d
j
T
A
d
j
,
j
=
0
,
1
,
?
?
,
k
?
1.
\begin{align} \beta_j=\frac{\nabla f(x_k)^TAd_j}{d_j^TAd_j},\quad j=0,1,\cdots,k-1.\end{align}
βj?=djT?Adj??f(xk?)TAdj??,j=0,1,?,k?1.??因此,只要按(5)取值
{
β
j
}
j
=
0
k
?
1
\{\beta_j\}_{j=0}^{k-1}
{βj?}j=0k?1?,向量组
d
0
,
?
?
,
d
k
?
1
,
d
k
d_0,\cdots,d_{k-1},d_k
d0?,?,dk?1?,dk? 就是彼此 (A) 共轭的.而且,根据命题 4.1中的
(
i
)
(i)
(i), 有
?
f
(
x
k
)
T
d
j
=
0
,
?
j
=
0
,
1
,
?
?
,
k
?
1
\nabla f(x_k)^Td_j=0,\:j=0,1,\cdots,k-1
?f(xk?)Tdj?=0,j=0,1,?,k?1. 从而
?
f
(
x
k
)
T
d
k
=
?
∥
?
f
(
x
k
)
∥
2
2
<
0.
\nabla f(x_k)^Td_k=-\|\nabla f(x_k)\|_2^2<0.
?f(xk?)Tdk?=?∥?f(xk?)∥22?<0.因而,通过精确搜索可得
α
k
>
0
\alpha_k>0
αk?>0, 使得
x
k
+
1
=
x
k
+
α
k
d
k
x_{k+1}=x_k+\alpha_kd_k
xk+1?=xk?+αk?dk? 满足
?
f
(
x
k
+
1
)
T
d
k
=
0.
\nabla f(x_{k+1})^Td_k=0.
?f(xk+1?)Tdk?=0.
进一步,若 ∥ ? f ( x k + 1 ) ∥ 2 ≥ ? \|\nabla f(x_{k+1})\|_2\geq\epsilon ∥?f(xk+1?)∥2?≥?, 重复上述过程,直至满足停止条件. 此算法利用梯度向量构造共轭向量组,故称之为共轭梯度法.
实际上,我们可以化简 { β j } \{\beta_{j}\} {βj?}的计算,首先根据目标函数的二次性可以知道:
? f ( x j + 1 ) = ? f ( x j ) + α j A d j , j = 0 , ? ? , k ? 1. \begin{align}\nabla f(x_{j+1})=\nabla f(x_j)+\alpha_jAd_j,\quad j=0,\cdots,k-1.\end{align} ?f(xj+1?)=?f(xj?)+αj?Adj?,j=0,?,k?1.??所以, 对 0 ≤ j ≤ k ? 2 0\leq j\leq k-2 0≤j≤k?2,因为 ? f ( x j ) = d j \nabla f(x_j)=d_j ?f(xj?)=dj?,有 A d j = α j ? 1 [ ? f ( x j + 1 ) ? ? f ( x j ) ] ∈ s p a n { d 0 , ? ? , d k ? 1 } . Ad_{j}=\alpha_{j}^{-1}[\nabla f(x_{j+1})-\nabla f(x_{j})]\in\mathbf{span}\{d_{0},\cdots,d_{k-1}\}. Adj?=αj?1?[?f(xj+1?)??f(xj?)]∈span{d0?,?,dk?1?}.再根据命题 命题 4.1 ( i ) 命题 4.1(i) 命题4.1(i) 即 ? f ( x k ) T d j = 0 , j = 0 , ? ? , k ? 1 \nabla f(x_k)^Td_j=0,j=0,\cdots,k-1 ?f(xk?)Tdj?=0,j=0,?,k?1,便可以得到 ? f ( x k ) ⊥ s p a n { d 0 , ? ? , d k ? 1 } \nabla f(x_k) \perp \mathbf{span}\{d_{0},\cdots,d_{k-1}\} ?f(xk?)⊥span{d0?,?,dk?1?},从而有 ? f ( x k ) T A d j = 0 \nabla f(x_{k})^{T}Ad_{j}=0 ?f(xk?)TAdj?=0,于是 β j = ? f ( x k ) T A d j d j T A d j = 0 \beta_j=\frac{\nabla f(x_k)^TAd_j}{d_{j}^TAd_j}=0 βj?=djT?Adj??f(xk?)TAdj??=0.
类似地,根据
d
k
?
1
d_{k-1}
dk?1?的定义式(4)
d
k
:
=
?
?
f
(
x
k
)
+
∑
i
=
0
k
?
1
β
i
d
i
d_k:=-\nabla f(x_k)+\sum_{i=0}^{k-1}\beta_id_i
dk?:=??f(xk?)+∑i=0k?1?βi?di?,可以知道
?
f
(
x
k
?
1
)
=
?
d
k
?
1
+
∑
i
=
0
k
?
1
β
i
d
i
=
A
x
k
?
1
+
b
∈
s
p
a
n
{
d
0
,
?
?
,
d
k
?
1
}
\nabla f(x_{k-1})=-d_{k-1}+\sum_{i=0}^{k-1}\beta_id_i=Ax_{k-1}+b \in \mathbf{span}\{d_{0},\cdots,d_{k-1}\}
?f(xk?1?)=?dk?1?+∑i=0k?1?βi?di?=Axk?1?+b∈span{d0?,?,dk?1?},所以有
A
d
k
?
1
=
α
k
?
1
?
1
[
?
f
(
x
k
)
?
?
f
(
x
k
?
1
)
]
∈
α
k
?
1
?
1
?
f
(
x
k
)
+
s
p
a
n
{
d
0
,
?
?
,
d
k
?
1
}
.
Ad_{k-1}=\alpha_{k-1}^{-1}[\nabla f(x_k)-\nabla f(x_{k-1})]\in\alpha_{k-1}^{-1}\nabla f(x_k)+\mathbf{span}\{d_0,\cdots,d_{k-1}\}.
Adk?1?=αk?1?1?[?f(xk?)??f(xk?1?)]∈αk?1?1??f(xk?)+span{d0?,?,dk?1?}.即
?
f
(
x
k
)
T
A
d
k
?
1
=
α
k
?
1
?
1
∥
?
f
(
x
k
)
∥
2
2
\nabla f(x_k)^TAd_{k-1}=\alpha_{k-1}^{-1}\|\nabla f(x_k)\|_2^2
?f(xk?)TAdk?1?=αk?1?1?∥?f(xk?)∥22?,从而
β
k
?
1
=
∥
?
f
(
x
k
)
∥
2
2
α
k
?
1
d
k
?
1
T
A
d
k
?
1
.
\beta_{k-1}=\frac{\|\nabla f(x_k)\|_2^2}{\alpha_{k-1}d_{k-1}^TAd_{k-1}}.
βk?1?=αk?1?dk?1T?Adk?1?∥?f(xk?)∥22??.根据最速下降法中的精确搜索公式即
α
k
:
=
argmin
?
α
>
0
f
(
x
k
+
α
d
k
)
=
?
(
A
x
k
+
b
)
T
d
k
d
k
T
A
d
k
=
?
?
f
(
x
k
)
T
d
k
d
k
T
A
d
k
\alpha_k:=\underset{\alpha>0}{\operatorname*{argmin}}f(x_k+\alpha d_k)=-\frac{(Ax_k+b)^Td_k}{d_k^TAd_k}=-\frac{\nabla f(x_k)^Td_k}{d_k^TAd_k}
αk?:=α>0argmin?f(xk?+αdk?)=?dkT?Adk?(Axk?+b)Tdk??=?dkT?Adk??f(xk?)Tdk??,可以得到
α
k
?
1
=
?
?
f
(
x
k
?
1
)
T
d
k
?
1
d
k
?
1
T
A
d
k
?
1
\alpha_{k-1}=-\frac{\nabla f(x_{k-1})^{T}d_{k-1}}{d_{k-1}^{T}Ad_{k-1}}
αk?1?=?dk?1T?Adk?1??f(xk?1?)Tdk?1?? 又因为有
?
f
(
x
k
?
1
)
T
d
k
?
1
=
?
∥
?
f
(
x
k
?
1
)
∥
2
2
\nabla f(x_{k-1})^Td_{k-1}=-\|\nabla f(x_{k-1})\|_2^2
?f(xk?1?)Tdk?1?=?∥?f(xk?1?)∥22?,所以
β
k
?
1
=
∥
?
f
(
x
k
)
∥
2
2
∥
?
f
(
x
k
?
1
)
∥
2
2
\beta_{k-1}=\frac{\|\nabla f(x_k)\|_2^2}{\|\nabla f(x_{k-1})\|_2^2}
βk?1?=∥?f(xk?1?)∥22?∥?f(xk?)∥22??以上便是
{
β
j
}
\{\beta_j\}
{βj?}的一种简化方法,这种方法称为Flecther-Reeves方法,简称为 F-R方法,实际上还有很多的关于待定系数
{
β
j
}
\{\beta_j\}
{βj?}的求法,在此不加证明指出各种求解待定系数的方法在函数为二次型,且使用精准线搜时完全等价.当然这里也列举一些,供读者查阅,各种方法如下所示(一般情况下,很多文章会以记号
g
k
g_k
gk? 来代替
f
(
x
k
)
f(x_k)
f(xk?))
β
k
?
1
H
S
=
?
f
(
x
k
)
T
A
?
f
(
x
k
?
1
)
d
k
?
1
T
A
d
k
?
1
(Hestenes
?
Stiefel公式)
β
k
?
1
C
W
=
?
f
(
x
k
)
T
(
?
f
(
x
k
)
?
?
f
(
x
k
?
1
)
)
d
k
?
1
T
(
?
f
(
x
k
)
?
?
f
(
x
k
?
1
)
)
(
Crowder
?
Wolfe公式
)
β
k
?
1
F
R
=
?
f
(
x
k
)
T
?
f
(
x
k
)
?
f
(
x
k
?
1
)
T
?
f
(
x
k
?
1
)
(
F
letcher
?
R
eeves公式
)
β
k
?
1
D
=
?
?
f
(
x
k
)
T
?
f
(
x
k
)
d
k
?
1
T
?
f
(
x
k
?
1
)
(Dixon公式)
β
k
?
1
P
R
l
P
=
?
f
(
x
k
)
T
(
?
f
(
x
k
)
?
?
f
(
x
k
?
1
)
)
?
f
(
x
k
?
1
)
T
?
f
(
x
k
?
1
)
(
P
o
l
a
k
?
R
i
b
i
e
r
e
?
P
o
l
y
a
k
公式
)
β
k
?
1
D
Y
=
?
f
(
x
k
)
T
?
f
(
x
k
)
d
k
?
1
T
(
?
f
(
x
k
)
?
?
f
(
x
k
?
1
)
)
(
D
a
i
?
Y
u
a
n
公式
)
\begin{aligned} \beta_{k-1}^{HS}& =\frac{\nabla f(x_{k})^TA\nabla f(x_{k-1})}{d_{k-1}^TAd_{k-1}}\quad\text{(Hestenes}-\text{Stiefel公式)} \\ \beta_{k-1}^{CW}& =\frac{\nabla f(x_{k})^T(\nabla f(x_{k})-\nabla f(x_{k-1}))}{d_{k-1}^T(\nabla f(x_{k})-\nabla f(x_{k-1}))}\quad(\textbf{Crowder}-\textbf{Wolfe公式}) \\ \beta_{k-1}^{FR}& =\frac{\nabla f(x_{k})^T\nabla f(x_{k})}{\nabla f(x_{k-1})^T\nabla f(x_{k-1})}\quad\quad(\mathbf{F}\text{letcher}-\mathbf{R}\text{eeves公式}) \\ \beta_{k-1}^{D}& =-\frac{\nabla f(x_{k})^T\nabla f(x_{k})}{d_{k-1}^T\nabla f(x_{k-1})}\quad\quad\quad\text{(Dixon公式)} \\ \beta_{k-1}^{PRl}& ^{P}=\frac{\nabla f(x_{k})^{T}(\nabla f(x_{k})-\nabla f(x_{k-1}))}{\nabla f(x_{k-1})^{T}\nabla f(x_{k-1})}\quad(\mathbf{Polak}-\mathbf{Ribiere}-\mathbf{Polyak}\text{公式}) \\ \beta_{k-1}^{DY}& =\frac{\nabla f(x_{k})^T\nabla f(x_{k})}{d_{k-1}^T(\nabla f(x_{k})-\nabla f(x_{k-1}))} (\mathbf{Dai}-\mathbf{Yuan}\text{公式}) \end{aligned}
βk?1HS?βk?1CW?βk?1FR?βk?1D?βk?1PRl?βk?1DY??=dk?1T?Adk?1??f(xk?)TA?f(xk?1?)?(Hestenes?Stiefel公式)=dk?1T?(?f(xk?)??f(xk?1?))?f(xk?)T(?f(xk?)??f(xk?1?))?(Crowder?Wolfe公式)=?f(xk?1?)T?f(xk?1?)?f(xk?)T?f(xk?)?(Fletcher?Reeves公式)=?dk?1T??f(xk?1?)?f(xk?)T?f(xk?)?(Dixon公式)P=?f(xk?1?)T?f(xk?1?)?f(xk?)T(?f(xk?)??f(xk?1?))?(Polak?Ribiere?Polyak公式)=dk?1T?(?f(xk?)??f(xk?1?))?f(xk?)T?f(xk?)?(Dai?Yuan公式)?
4.3 共轭梯度法的程序实现
现在总结一下,目标函数为二次型,基于F-R方法的共轭梯度算法如下:
算法 4.1 (共轭梯度法) 取充分小的数
?
>
0.
\epsilon>0.
?>0.
第 1 \mathscr{1} 1 步:任取 x 0 ∈ R n x_0\in\mathbb{R}^n x0?∈Rn,令 k = 0. k=0. k=0.
第 2 \mathscr{2} 2 步:若 ∥ ? f ( x k ) ∥ < ? \|\nabla f(x_k)\|<\epsilon ∥?f(xk?)∥<?,转第 4 \mathscr{4} 4 步;否则,令 d k : = { ? ? f ( x k ) k = 0 , ? ? f ( x k ) + β k ? 1 d k ? 1 k ≥ 1 , 其中 β k ? 1 : = ∥ ? f ( x k ) ∥ 2 ∥ ? f ( x k ? 1 ) ∥ 2 d_k:=\begin{align}\begin{cases}-\nabla f(x_k)&k=0,\\-\nabla f(x_k)+\beta_{k-1}d_{k-1}&k\ge1,\end{cases}\quad\text{其中}\quad\beta_{k-1}:=\frac{\|\nabla f(x_k)\|^2}{\|\nabla f(x_{k-1})\|^2}\end{align} dk?:={??f(xk?)??f(xk?)+βk?1?dk?1??k=0,k≥1,?其中βk?1?:=∥?f(xk?1?)∥2∥?f(xk?)∥2???
第 3 \mathscr{3} 3 步:通过精确搜索计算 x k + 1 = x k + α k d k x_{k+1}=x_k+\alpha_kd_k xk+1?=xk?+αk?dk?,其中 α k = ∥ ? f ( x k ) ∥ 2 2 d k T A d k \alpha_k=\frac{\|\nabla f(x_k)\|_2^2}{d_k^TAd_k} αk?=dkT?Adk?∥?f(xk?)∥22??并计算 ? f ( x k + 1 ) : = A x k + 1 + b \nabla f(x_{k+1}):=Ax_{k+1}+b ?f(xk+1?):=Axk+1?+b.令 k = k + 1 k=k+1 k=k+1,转第 2 \mathscr{2} 2 步.
第 4 \mathscr{4} 4 步:输出极小值点 x k x_k xk?. 程序结束.
设需要最小化的目标二次函数如下:
f
(
x
)
=
1
2
x
T
A
x
+
b
T
x
,
Q
=
(
3
?
1
?
1
1
)
,
b
=
(
2
,
0
)
T
f(x)=\frac12x^TAx+b^Tx,Q=\begin{pmatrix}3&-1\\-1&1\end{pmatrix},b=(2,0)^T
f(x)=21?xTAx+bTx,Q=(3?1??11?),b=(2,0)T即
min
?
f
(
x
)
=
3
2
x
1
2
+
1
2
x
2
2
?
x
1
x
2
?
2
x
1
\min f(x)=\frac32x_1^2+\frac12x_2^2-x_1x_2-2x_1
minf(x)=23?x12?+21?x22??x1?x2??2x1?为了检验迭代过程的可靠性,我们可以解析地求出该优化问题的最优点:
x
?
=
?
A
?
1
b
=
(
1
,
1
)
T
x^*=-A^{-1}b=(1,1)^T
x?=?A?1b=(1,1)T此外我们还需要定义目标函数中的
A
,
b
A,b
A,b 还有原本的函数
f
f
f 和函数梯度
?
f
\nabla f
?f 的映射func和gradient.准备工作部分的代码如下:
# 准备工作
import numpy as np
import matplotlib.pyplot as plt
A = np.array([[3, -1], [-1, 1]], dtype="float32") # 定义矩阵 A
b = np.array([-2, 0], dtype="float32").reshape([-1, 1]) # 向量b
# function and its gradient defined in the question
func = lambda x: 0.5 * np.dot(x.T, np.dot(A, x)).squeeze() + np.dot(b.T, x).squeeze() # 函数
gradient = lambda x: np.dot(A, x) + b # 梯度
x_0 = np.array([1, 1]).reshape([-1, 1]) # 最优点x_0
准备工作完成后,编写基于精确搜索的最速下降法的函数实现:
# FGCG algorithm
def FGCG(start_point, func, gradient, epsilon=0.01):
"""
:param start_point: start point of GD 初始值
:param func: map of plain function 目标函数
:param gradient: gradient map of plain function 梯度函数
:param epsilon: threshold to stop the iteration 迭代终止的阈值
:return: converge point, # iterations
"""
assert isinstance(start_point, np.ndarray) # assert that input start point is ndarray
global Q, b, x_0 # claim the global varience
x_k_1, iter_num, loss = start_point, 0, []
xs = [x_k_1] # xs是迭代点的序列,最后一个就是最后一次求的点
# 初始化
g_k_list = [] # g_k = delta f(x_k),改变用来储存梯度向量
g_k_list.append(gradient(start_point).reshape([-1, 1]))
d_k_list = [] # 储存搜索方向的list
d_k_list.append(-gradient(start_point).reshape([-1, 1]))
while True:
g_k = g_k_list[iter_num]
d_k = d_k_list[iter_num]
if np.sqrt(np.sum(g_k ** 2)) < epsilon: # 终止条件(1)
break
if len(g_k) > 1:
g_k_1 = g_k_list[iter_num-1] # 取出delta f_x_{k-1}
beta = np.sum(g_k ** 2) / np.sum(g_k_1 ** 2)
d_current = -g_k + beta * d_k # 当前迭代的搜索方向d_k
d_k = d_current
d_k_list.append(d_k)
alpha_k = np.dot(g_k.T, g_k).squeeze() / (np.dot(d_k.T, np.dot(A, d_k))).squeeze() # 精确搜索计算步长alpha_k
x_k_2 = x_k_1 + alpha_k * d_k # 迭代式
iter_num += 1
xs.append(x_k_2)
g_k_list.append(gradient(x_k_2).reshape([-1, 1])) # 计算delta f(x_{k+1}=Ax_{k+1}+b)
loss.append(float(np.fabs(func(x_k_2) - func(x_0))))
if np.fabs(func(x_k_2) - func(x_k_1)) < epsilon:
break
if iter_num > 100: # 超过一定次数后停止迭代
break
x_k_1 = x_k_2
return xs, iter_num, loss
假设此处的迭代初值为? x 0 = ( 4 , 5 ) T x_0=(4,5)^T x0?=(4,5)T ,进行梯度下降法,并可视化迭代过程:
x0 = np.array([4,5], dtype="float32").reshape([-1, 1]) # 定义初始值
xs, iter_num, loss = gradient_descent(start_point=x0,
func=func,
gradient=gradient,
epsilon=1e-6) # 传入参数
print(xs[-1]) # last point of the sequence 输出迭代点列的最后一个值
plt.style.use("seaborn") # 样式
plt.figure(figsize=[12, 6]) # 图像大小
plt.plot(loss)
plt.xlabel("# iteration", fontsize=12)
plt.ylabel("Loss: $|f(x_k) - f(x^*)|$", fontsize=12)
plt.yscale("log")
plt.show()
def text_plot():
# 画出点图
print(xs[-1]) # last point of the sequence 输出迭代点列的最后一个值
x = []
y = []
for i in xs:
x.append( i[0])
y.append( i[1])
plt.style.use("seaborn") # 样式
plt.figure(figsize=[12, 6]) # 图像大小
plt.plot(x,y)
plt.xlabel("x", fontsize=12)
plt.ylabel("y", fontsize=12)
# plt.yscale("log")
plt.show()
运行结果:
[[0.9999299]
[1.0005273]]
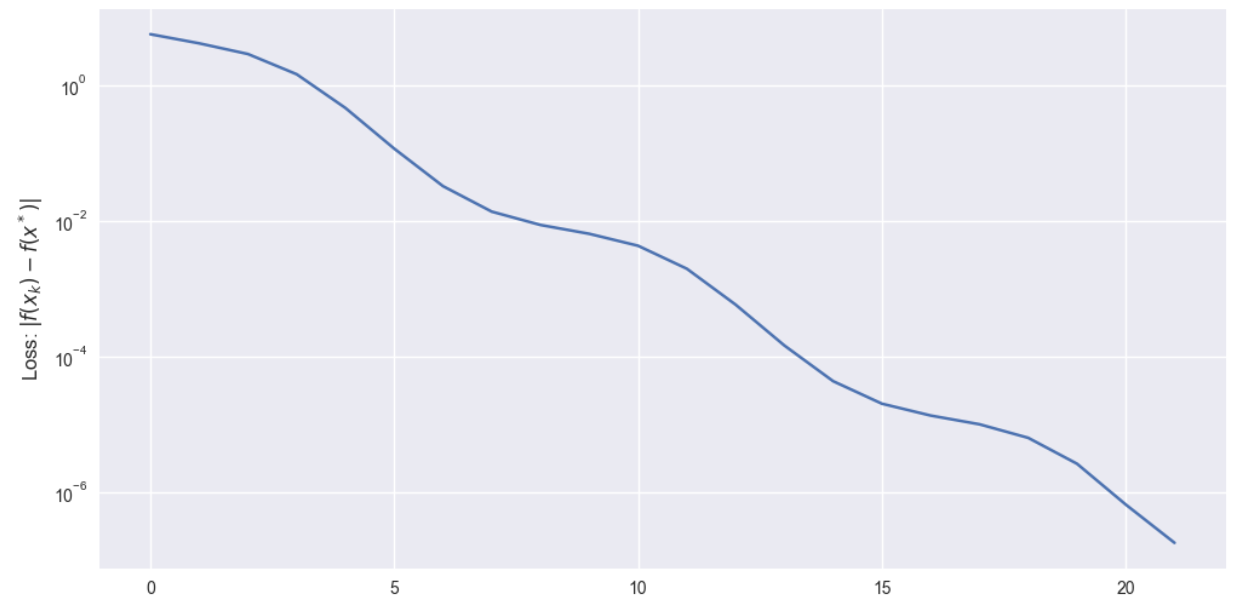
可以看到最终迭代点到达了最优点 ( 1 , 1 ) T (1,1)^T (1,1)T。当纵坐标取对数 l o g log log 时,loss是在不断下降的。我们再更换几组初始点,并把相关的参数画在一个图像内看看效果.
我们再取四个迭代点:? ( 0 , 0 ) , ( 0.4 , 0 ) , ( 10 , 0 ) , ( 11 , 0 ) (0,0),(0.4,0),(10,0),(11,0) (0,0),(0.4,0),(10,0),(11,0)
# create the list of all starting point x_0
starting_points = [np.array([num, 0]).astype(np.float).reshape([-1, 1]) for num in [0.0, 0.4, 10.0, 11.0]]
plt.figure(dpi=150)
xss = []
# implement FGCG
for idx, start_point in enumerate(starting_points):
xs, iter_num, losses = gradient_descent(start_point, func, gradient, epsilon=1e-6)
target_point = xs[-1]
xss.append(xs)
# plot the losses of $|f(x_k) - f(x^*)|$
plt.plot(np.arange(len(losses)), np.array(losses), label=f"start point: ({start_point[0][0]}, {start_point[1][0]})")
loss = np.fabs(func(target_point) - func(x_0))
print(f"{idx + 1}: start point:{np.round(start_point, 5).tolist()}, "
f"point after GD:{np.round(target_point, 5).tolist()}, "
f"loss:{np.round(loss, 16)}, # iterations: {iter_num}")
print("-" * 60)
plt.grid(True)
plt.legend()
plt.xlabel("# iteration", fontsize=12)
plt.ylabel("Loss: $|f(x_k) - f(x^*)|$", fontsize=12)
plt.yscale("log")
plt.title("Loss-iteration given to different starting points of GD", fontsize=18)
plt.show()
输出结果:
1: start point:[[0.0], [0.0]], point after FGCG:[[0.99964], [0.99972]], loss:1.324470967e-07, # iterations: 19
------------------------------------------------------------
2: start point:[[0.4], [0.0]], point after FGCG:[[0.99978], [0.99922]], loss:2.053100269e-07, # iterations: 17
------------------------------------------------------------
3: start point:[[10.0], [0.0]], point after FGCG:[[0.9998], [1.00051]], loss:2.990393975e-07, # iterations: 19
------------------------------------------------------------
4: start point:[[11.0], [0.0]], point after FGCG:[[0.9998], [1.00062]], loss:3.793825739e-07, # iterations: 19
------------------------------------------------------------

由上图可以看到可以看到不同的初值点,收敛速率并不像最速下降法一样显著不相同。也就是说不同的初始点到达最优点的所需的迭代次数基本是相同的.下面把上述过程在二维平面内可视化出来:
plt.figure(dpi=150)
X = np.linspace(-2, 12, 200)
Y = np.linspace(-2, 12, 200)
XX, YY = np.meshgrid(X, Y)
Z = [func(np.array([XX[i, j], YY[i, j]], dtype="float32").reshape([-1, 1])).tolist() for i in range(200) for j in range(200)]
Z = np.array(Z).reshape([200, 200])
plt.contourf(XX, YY, Z, cmap=plt.cm.BuGn)
plt.annotate(f"$(5.0, 6.0)$",
xy=(5, 6),
xytext=(5 - 2, 6 + 2),
arrowprops={
"color" : "black",
"shrink" : 0.1,
"width" : 0.6
})
# plot the scatter
for idx, start_point in enumerate(starting_points):
xx = [xss[idx][i][0] for i, _ in enumerate(xss[idx])]
yy = [xss[idx][i][1] for i, _ in enumerate(xss[idx])]
plt.plot(xx, yy, "o--", label=f"start point: ({start_point[0][0]}, {start_point[1][0]})")
# add some tips for start point
plt.annotate(f"$({start_point[0][0]}, {start_point[1][0]})$",
xy=(start_point[0][0], start_point[1][0]),
xytext=(start_point[0][0] - 1.5, start_point[1][0] + idx + 2),
arrowprops={
"color" : "black",
"shrink" : 0.1,
"width" : 0.6
})
plt.grid(True)
plt.title("FGCG For Two-dimensional Diagrams", fontsize=18)
plt.xlabel("$x_1$", fontsize=12)
plt.ylabel("$x_2$", fontsize=12)
plt.legend()
plt.show()
运行结果:
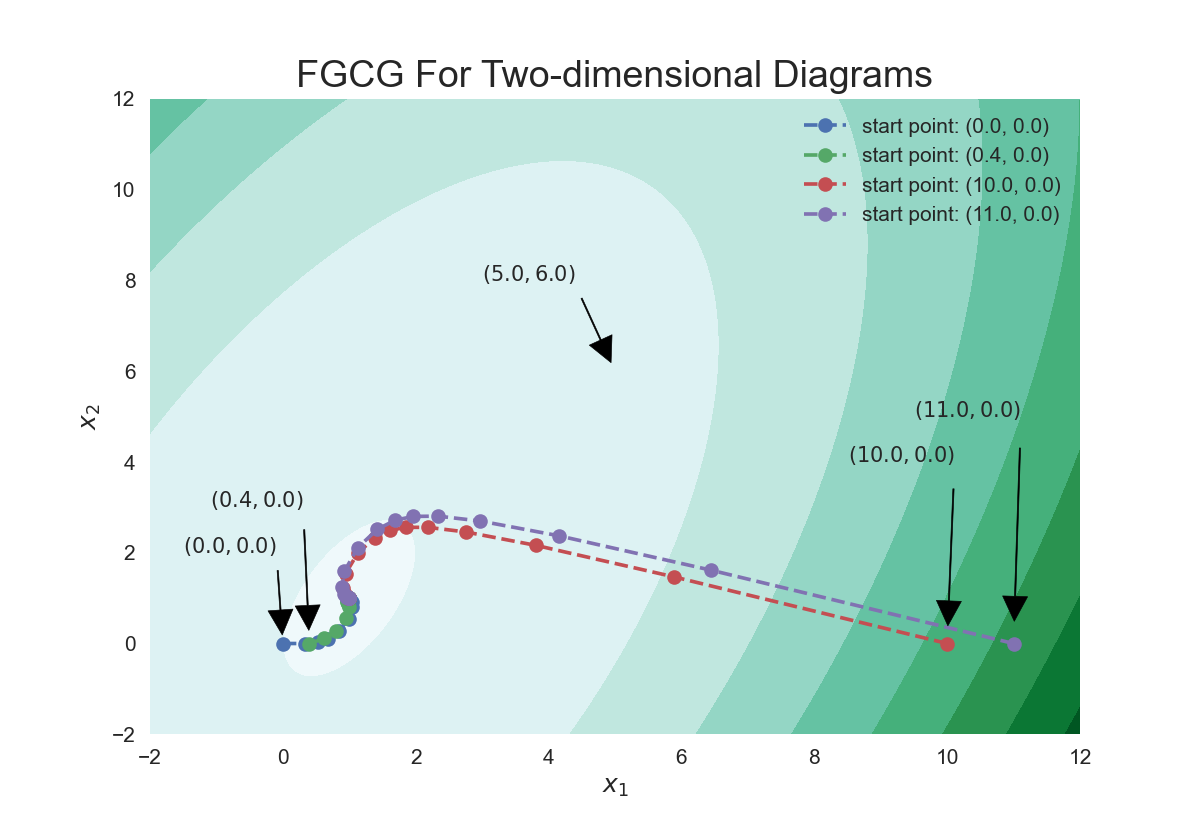
这张图可以直观地感受四个迭代点的迭代步数并没有显著的差距。究其原因,由于共轭梯度法中关于搜索方向的选择基本是一致的,所以初始点的选择对于迭代过程的影响很小,接下来我们看看非二次函数的共轭梯度法的以及F-R方法收敛性的证明.
4.4 非二次函数的共轭梯度法
共轭梯度法的迭代公式
d
0
:
=
?
?
f
(
x
0
)
,
d
k
:
=
?
?
f
(
x
k
)
+
β
k
?
1
d
k
?
1
,
β
k
?
1
:
=
∥
?
f
(
x
k
)
∥
2
2
∥
?
f
(
x
k
?
1
)
∥
2
2
\begin{align}d_0:=-\nabla f(x_0),\quad d_k:=-\nabla f(x_k)+\beta_{k-1}d_{k-1},\quad\beta_{k-1}:=\frac{\|\nabla f(x_k)\|_2^2}{\|\nabla f(x_{k-1})\|_2^2}\end{align}
d0?:=??f(x0?),dk?:=??f(xk?)+βk?1?dk?1?,βk?1?:=∥?f(xk?1?)∥22?∥?f(xk?)∥22????中不含有矩阵
A
A
A,这说明当目标函数不是二次函数时,形式上基于F-G方法的共轭梯度法仍然可用而且当线搜索采用精确搜索时,它具有二次终止性.下面我们研究共轭梯度法公式(8)对于非二次函数的收敛性.对于一般的目标函数
f
(
x
)
f(x)
f(x) 求精确搜索
x
k
+
1
=
x
k
+
α
k
d
k
x_{k+1} = x_k + α_kd_k
xk+1?=xk?+αk?dk? 本身也是一个优化问题,且该优化问题具有较大的计算复杂性,所以,下面我们将步长的确定不限于精确搜索.
我们在之前的学习笔记中说到过,线搜索迭代方法的收敛的一个关键条件是所谓的一致锐角条件:记
g
k
:
=
?
f
(
x
k
)
g_k:=\nabla f(x_k)
gk?:=?f(xk?),
g
k
T
d
k
=
∥
g
k
∥
2
cos
?
θ
k
≥
∥
g
k
∥
2
cos
?
(
π
2
?
μ
)
=
∥
g
k
∥
2
sin
?
μ
g_k^Td_k=\|g_k\|_2\cos\theta_k\geq\|g_k\|_2\cos(\frac{\pi}{2}-\mu)=\|g_k\|_2\sin\mu
gkT?dk?=∥gk?∥2?cosθk?≥∥gk?∥2?cos(2π??μ)=∥gk?∥2?sinμ,于是
g
k
T
d
k
≥
∥
g
k
∥
2
sin
?
μ
g_k^Td_k\geq\|g_k\|_2\sin\mu
gkT?dk?≥∥gk?∥2?sinμ或较
弱一点的条件:若
∥
?
f
(
x
k
)
∥
2
≠
0
,
?
?
k
≥
0
\|\nabla f(x_k)\|_2\neq0,~\forall k\geq0
∥?f(xk?)∥2?=0,??k≥0, 且满足条件
∑
k
=
1
∞
cos
?
2
θ
k
=
∞
.
\sum_{k=1}^\infty\cos^2\theta_k=\infty.
∑k=1∞?cos2θk?=∞.
为此我们看看如下的引理
引理 4.2 设
f
∈
C
1
(
R
n
)
,
?
x
0
∈
R
n
,
?
∥
?
f
(
x
0
)
∥
≠
0
f\in C^1(\mathbb{R}^n),~x_0\in\mathbb{R}^n,~\|\nabla f(x_0)\|\neq0
f∈C1(Rn),?x0?∈Rn,?∥?f(x0?)∥=0. 设
d
k
d_k
dk? 由共轭梯度法公式(8)求得,线搜索
x
k
=
x
k
?
1
+
α
k
?
1
d
k
?
1
x_k=x_{k-1}+\alpha_{k-1}d_{k-1}
xk?=xk?1?+αk?1?dk?1?,满足
∥
?
f
(
x
j
)
∥
≠
0
,
∣
?
f
(
x
j
)
T
d
j
?
1
∣
≤
?
σ
?
f
(
x
j
?
1
)
T
d
j
?
1
,
j
=
1
,
?
?
,
k
,
\begin{align} \|\nabla f(x_j)\|\neq0,\quad|\nabla f(x_j)^Td_{j-1}|\le-\sigma\nabla f(x_{j-1})^Td_{j-1},\quad j=1,\cdots,k,\end{align}
∥?f(xj?)∥=0,∣?f(xj?)Tdj?1?∣≤?σ?f(xj?1?)Tdj?1?,j=1,?,k,??其中
σ
∈
[
0
,
1
)
\sigma\in[0,1)
σ∈[0,1),那么
1
?
2
σ
1
?
σ
∥
?
f
(
x
k
)
∥
2
≤
?
?
f
(
x
k
)
T
d
k
≤
1
1
?
σ
∥
?
f
(
x
k
)
∥
2
,
k
=
1
,
2
,
?
\begin{align}\frac{1-2\sigma}{1-\sigma}\|\nabla f(x_k)\|^2\leq-\nabla f(x_k)^Td_k\leq\frac1{1-\sigma}\|\nabla f(x_k)\|^2,\quad k=1,2,\cdots\end{align}
1?σ1?2σ?∥?f(xk?)∥2≤??f(xk?)Tdk?≤1?σ1?∥?f(xk?)∥2,k=1,2,???且有
∥
?
f
(
x
k
)
∥
4
∥
d
k
∥
2
≥
1
?
σ
1
+
σ
(
∑
j
=
0
k
∥
?
f
(
x
j
)
∥
?
2
)
?
1
.
\begin{align}\frac{\|\nabla f(x_k)\|^4}{\|d_k\|^2}\geq\frac{1-\sigma}{1+\sigma}\Big(\sum_{j=0}^k\|\nabla f(x_j)\|^{-2}\Big)^{-1}.\end{align}
∥dk?∥2∥?f(xk?)∥4?≥1+σ1?σ?(j=0∑k?∥?f(xj?)∥?2)?1.??
证. 记 g k : = ? f ( x k ) , ? k = 0 , 1 , ? g_k:=\nabla f(x_k),\:k=0,1,\cdots gk?:=?f(xk?),k=0,1,?. 先证(10). 不妨设 ∥ g k ∥ ≠ 0 \|g_k\|\neq0 ∥gk?∥=0. 等式 d k = d_k= dk?= ? g k + β k ? 1 d k ? 1 -g_k+\beta_{k-1}d_{k-1} ?gk?+βk?1?dk?1? 两边与 g k g_k gk? 做内积,得 ∣ g k T d k + g k T g k ∣ = β k ? 1 ∣ g k T d k ? 1 ∣ ≤ ? σ β k ? 1 g k ? 1 T d k ? 1 = ? σ ( g k T g k ) ( g k ? 1 T d k ? 1 ) g k ? 1 T g k ? 1 . |g_k^Td_k+g_k^Tg_k|=\beta_{k-1}|g_k^Td_{k-1}|\leq-\sigma\beta_{k-1}g_{k-1}^Td_{k-1}=-\sigma\frac{(g_k^Tg_k)(g_{k-1}^Td_{k-1})}{g_{k-1}^Tg_{k-1}}. ∣gkT?dk?+gkT?gk?∣=βk?1?∣gkT?dk?1?∣≤?σβk?1?gk?1T?dk?1?=?σgk?1T?gk?1?(gkT?gk?)(gk?1T?dk?1?)?.即 ∣ g k T d k g k T g k + 1 ∣ ≤ ? σ g k ? 1 T d k ? 1 g k ? 1 T g k ? 1 = σ ? σ ( g k ? 1 T d k ? 1 g k ? 1 T g k ? 1 + 1 ) ≤ σ + σ ∣ g k ? 1 T d k ? 1 g k ? 1 T g k ? 1 + 1 ∣ . \left|\frac{g_k^Td_k}{g_k^Tg_k}+1\right|\leq-\sigma\frac{g_{k-1}^Td_{k-1}}{g_{k-1}^Tg_{k-1}}=\sigma-\sigma\left(\frac{g_{k-1}^Td_{k-1}}{g_{k-1}^Tg_{k-1}}+1\right)\leq\sigma+\sigma\left|\frac{g_{k-1}^Td_{k-1}}{g_{k-1}^Tg_{k-1}}+1\right|. ?gkT?gk?gkT?dk??+1 ?≤?σgk?1T?gk?1?gk?1T?dk?1??=σ?σ(gk?1T?gk?1?gk?1T?dk?1??+1)≤σ+σ ?gk?1T?gk?1?gk?1T?dk?1??+1 ?.据此递推关系,并注意到 g 0 T d 0 / ( g 0 T g 0 ) + 1 = 0 g_0^Td_0/(g_0^Tg_0)+1=0 g0T?d0?/(g0T?g0?)+1=0, 可得
∣ g k T d k g k T g k + 1 ∣ ≤ σ + σ 2 + ? + σ k = σ 1 ? σ . \left|\frac{g_k^Td_k}{g_k^Tg_k}+1\right|\leq\sigma+\sigma^2+\cdots+\sigma^k=\frac\sigma{1-\sigma}. ?gkT?gk?gkT?dk??+1 ?≤σ+σ2+?+σk=1?σσ?.将不等式(10)化简即发现和该式等价.
下面证明不等式
(
11
)
.
k
=
0
(11).\quad k=0
(11).k=0 时有
d
0
=
?
?
f
(
x
0
)
d_0=-\nabla f(x_0)
d0?=??f(x0?), 不等式显然成立. 下面设
k
≥
1
k\geq1
k≥1, 并假设不等式(11)对
k
?
1
k-1
k?1 成立. 利用(8)得 (注意,由于未必是精确搜索,条件
g
k
T
d
k
?
1
=
0
g_k^Td_{k-1}=0
gkT?dk?1?=0 不一定成立)
∥
d
k
∥
2
2
=
∥
g
k
∥
2
2
+
β
k
?
1
2
∥
d
k
?
1
∥
2
2
?
2
β
k
?
1
g
k
T
d
k
?
1
≤
∥
g
k
∥
2
2
+
β
k
?
1
2
∥
d
k
?
1
∥
2
2
?
2
σ
β
k
?
1
g
k
?
1
T
d
k
?
1
=
∥
g
k
∥
2
2
+
(
∥
g
k
∥
2
∥
g
k
?
1
∥
2
)
4
∥
d
k
?
1
∥
2
2
?
2
σ
(
∥
g
k
∥
2
∥
g
k
?
1
∥
2
)
2
g
k
?
1
T
d
k
?
1
.
\begin{aligned} \|d_{k}\|_{2}^{2}& =\|g_k\|_2^2+\beta_{k-1}^2\|d_{k-1}\|_2^2-2\beta_{k-1}g_k^Td_{k-1} \\ &\leq\|g_k\|_2^2+\beta_{k-1}^2\|d_{k-1}\|_2^2-2\sigma\beta_{k-1}g_{k-1}^Td_{k-1} \\ &=\|g_k\|_2^2+\left(\frac{\|g_k\|_2}{\|g_{k-1}\|_2}\right)^4\|d_{k-1}\|_2^2-2\sigma\Big(\frac{\|g_k\|_2}{\|g_{k-1}\|_2}\Big)^2g_{k-1}^Td_{k-1}. \end{aligned}
∥dk?∥22??=∥gk?∥22?+βk?12?∥dk?1?∥22??2βk?1?gkT?dk?1?≤∥gk?∥22?+βk?12?∥dk?1?∥22??2σβk?1?gk?1T?dk?1?=∥gk?∥22?+(∥gk?1?∥2?∥gk?∥2??)4∥dk?1?∥22??2σ(∥gk?1?∥2?∥gk?∥2??)2gk?1T?dk?1?.?利用
k
?
1
k-1
k?1 情形的不等式(10),得
g
k
?
1
T
d
k
?
1
≤
1
1
?
σ
∥
g
k
?
1
∥
2
2
g_{k-1}^Td_{k-1}\leq\frac1{1-\sigma}\|g_{k-1}\|_2^2
gk?1T?dk?1?≤1?σ1?∥gk?1?∥22?.代入上式,有
∥
d
k
∥
2
2
≤
1
+
σ
1
?
σ
∥
g
k
∥
2
2
+
∥
g
k
∥
2
4
?
∥
d
k
?
1
∥
2
2
∥
g
k
?
1
∥
2
4
.
\|d_k\|_2^2\leq\frac{1+\sigma}{1-\sigma}\|g_k\|_2^2+\|g_k\|_2^4\cdot\frac{\|d_{k-1}\|_2^2}{\|g_{k-1}\|_2^4}.
∥dk?∥22?≤1?σ1+σ?∥gk?∥22?+∥gk?∥24??∥gk?1?∥24?∥dk?1?∥22??.
根据
k
?
1
k-1
k?1 情形的归纳假设,得
∥
d
k
∥
2
2
≤
1
+
σ
1
?
σ
∥
g
k
∥
2
2
+
∥
g
k
∥
2
4
1
+
σ
1
?
σ
∑
j
=
0
k
?
1
∥
g
j
∥
2
?
2
=
1
+
σ
1
?
σ
∥
g
k
∥
2
4
∑
j
=
0
k
∥
g
j
∥
2
?
2
.
\|d_k\|_2^2\leq\frac{1+\sigma}{1-\sigma}\|g_k\|_2^2+\|g_k\|_2^4\frac{1+\sigma}{1-\sigma}\sum_{j=0}^{k-1}\|g_j\|_2^{-2}=\frac{1+\sigma}{1-\sigma}\|g_k\|_2^4\sum_{j=0}^k\|g_j\|_2^{-2}.
∥dk?∥22?≤1?σ1+σ?∥gk?∥22?+∥gk?∥24?1?σ1+σ?j=0∑k?1?∥gj?∥2?2?=1?σ1+σ?∥gk?∥24?j=0∑k?∥gj?∥2?2?. 所以,不等式(11)对
k
k
k 成立.引理证毕.
注:显然,精确搜索和强 Wolfe 搜索均满足条件
∣
?
f
(
x
k
)
T
d
k
?
1
∣
≤
?
σ
?
f
(
x
k
?
1
)
T
d
k
?
1
,
σ
∈
[
0
,
1
)
.
\begin{aligned}|\nabla f(x_k)^Td_{k-1}|\le-\sigma\nabla f(x_{k-1})^Td_{k-1},\quad\sigma\in[0,1).\end{aligned}
∣?f(xk?)Tdk?1?∣≤?σ?f(xk?1?)Tdk?1?,σ∈[0,1).?
命题 4.3 (F-R 方法的收敛性) 设 f ∈ C 1 ( R n ) f\in C^1(\mathbb{R}^n) f∈C1(Rn) 有下界, x 0 ∈ R n x_0\in\mathbb{R}^n x0?∈Rn, 梯度向量 ? f ( x ) \nabla f(x) ?f(x) 在包含水平集 lev f ( x 0 ) ( f ) _{f(x_0)}(f) f(x0?)?(f) 的一个凸集 D D D 上 L i p s c h i t z Lipschitz Lipschitz 连续. 设 d k d_k dk? 由共轭梯度法公式(8.4.8)求得,线搜索 x k = x k ? 1 + α k ? 1 d k ? 1 x_k=x_{k-1}+\alpha_{k-1}d_{k-1} xk?=xk?1?+αk?1?dk?1? 为精确搜索或参数 σ ∈ [ 0 , 1 / 2 ) \sigma\in[0,1/2) σ∈[0,1/2) 的强 W o l f e Wolfe Wolfe 搜索,那么,或者存在 k ≥ 0 k\geq0 k≥0,使得 ∥ ? f ( x k ) ∥ 2 = 0 \|\nabla f(x_k)\|_2=0 ∥?f(xk?)∥2?=0,或者 lim ? k → ∞ ∥ ? f ( x k ) ∥ 2  ̄ = 0. \underline{\lim_{k\to\infty}\|\nabla f(x_k)\|_2}=0. limk→∞?∥?f(xk?)∥2??=0.
证. 若结论不成立,则存在
δ
>
0
\delta>0
δ>0,使得
∥
?
f
(
x
j
)
∥
2
≥
δ
,
?
?
j
≥
0
\|\nabla f(x_j)\|_2\geq\delta,~\forall j\geq0
∥?f(xj?)∥2?≥δ,??j≥0. 对任意的
k
≥
0
k\geq0
k≥0,利用引理 4.2之结论 (10)可知
?
?
f
(
x
k
)
-\nabla f(x_k)
??f(xk?) 与
d
k
d_k
dk? 的夹角余弦满足
∥
?
f
(
x
k
)
∥
2
2
cos
?
2
θ
k
≥
(
1
?
2
σ
1
?
σ
)
2
∥
?
f
(
x
k
)
∥
2
4
∥
d
k
∥
2
2
.
\|\nabla f(x_k)\|_2^2\cos^2\theta_k\geq\left(\frac{1-2\sigma}{1-\sigma}\right)^2\frac{\|\nabla f(x_k)\|_2^4}{\|d_k\|_2^2}.
∥?f(xk?)∥22?cos2θk?≥(1?σ1?2σ?)2∥dk?∥22?∥?f(xk?)∥24??.进一步,利用(11)可得
∥
?
f
(
x
k
)
∥
2
4
∥
d
k
∥
2
2
≥
1
?
σ
1
+
σ
(
∑
j
=
0
k
∥
?
f
(
x
j
)
∥
2
?
2
)
?
1
≥
1
?
σ
1
+
σ
?
δ
2
k
+
1
.
\frac{\|\nabla f(x_k)\|_2^4}{\|d_k\|_2^2}\geq\frac{1-\sigma}{1+\sigma}\Big(\sum_{j=0}^k\|\nabla f(x_j)\|_2^{-2}\Big)^{-1}\geq\frac{1-\sigma}{1+\sigma}\cdot\frac{\delta^2}{k+1}.
∥dk?∥22?∥?f(xk?)∥24??≥1+σ1?σ?(j=0∑k?∥?f(xj?)∥2?2?)?1≥1+σ1?σ??k+1δ2?.所以
∑
k
=
0
∞
∥
?
f
(
x
k
)
∥
2
2
cos
?
2
θ
k
=
∞
.
\sum_{k=0}^\infty\|\nabla f(x_k)\|_2^2\cos^2\theta_k=\infty.
∑k=0∞?∥?f(xk?)∥22?cos2θk?=∞.
另一方面,由强 Wolfe 准则 ∣ ? f ( x k + 1 ) T d k ∣ ≤ ? σ ? f ( x k ) T d k |\nabla f(x_{k+1})^Td_k|\leq-\sigma\nabla f(x_k)^Td_k ∣?f(xk+1?)Tdk?∣≤?σ?f(xk?)Tdk? 可知 ? f ( x k ) T d k < 0 \nabla f(x_k)^Td_k<0 ?f(xk?)Tdk?<0.根据命题 2.2.4我们有 ∑ k = 0 ∞ ∥ ? f ( x k ) ∥ 2 2 cos ? 2 θ k < ∞ \sum_{k=0}^\infty\|\nabla f(x_k)\|_2^2\cos^2\theta_k<\infty ∑k=0∞?∥?f(xk?)∥22?cos2θk?<∞,矛盾.
Reference
本笔记内容的程序实现部分参考如下了文章:
最优化方法复习笔记(一)梯度下降法、精确线搜索与非精确线搜索(推导+程序)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!