算法设计与分析基础实验报告（三）

一.实验内容

1. 用程序实现插入排序的递归与非递归算法，并分别画出程序运行时间t与元素个数的曲线图.
2. ?实验中是否遇到相关问题，并分析出现该问题的原因

二.实验过程及记录结果

1. 递归算法进行插入排序代码：

??//递归

void insertionSortRecursive(int arr[], int n) {

????if (n <= 1) return;

????insertionSortRecursive(arr, n-1);

????int last = arr[n-1];

????int j = n-2;

????while (j >= 0 && arr[j] > last) {

????????swap(&arr[j], &arr[j+1]);

????????j--;

????}

}

2.非递归（迭代）算法进行插入排序代码：?

????????????

//非递归

void insertionSort(int arr[], int n) {

????int i, key, j;

????for (i = 1; i < n; i++) {

????????key = arr[i];

????????j = i - 1;

????????while (j >= 0 && arr[j] > key) {

????????????arr[j + 1] = arr[j];

????????????j = j - 1;

????????}

????????arr[j + 1] = key;

????}

} ??????????????????

3.运行时间t与元素个数的曲线图：

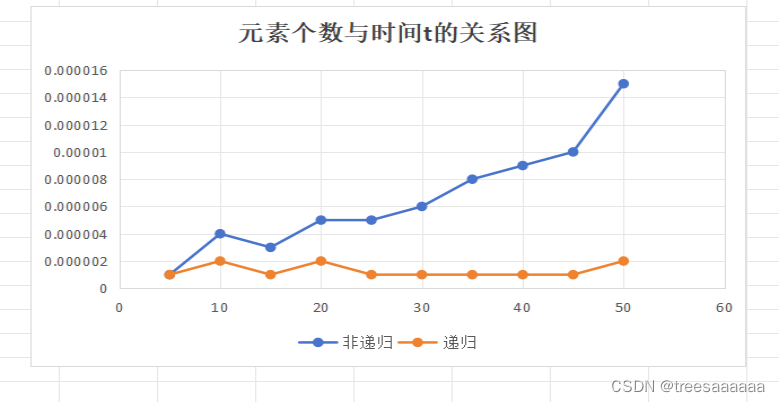
4.实验结果：由运行结果可视化分析可以得出：

这两种排序方法的时间复杂度都是O(n^2)，随着输入元素个数的增加，运行时间也会线性增加。这是因为在最坏的情况下，对于每个元素，都需要与其他所有元素进行比较和交换。

5.原因分析：

? ? (1)递归算法

对于递归实现，假设输入的元素个数为n，那么递归的深度将达到n，因为每次递归调用都会减少一个元素。由于每次递归调用都需要进行参数传递、栈空间分配、返回值处理等操作，因此递归的时间复杂度为O(n^2)。随着输入元素个数的增加，运行时间将呈二次方增长。

? ?(2)迭代算法

对于迭代实现，只需要一个循环就可以完成所有元素的排序。因此，迭代的时间复杂度为O(n^2)，与递归实现相同。但是，由于迭代没有进行递归调用，因此不会出现递归调用带来的额外开销。

6.总结

尽管迭代和递归的实现时间复杂度相同，但迭代实现的效率通常比递归实现更高。