【史上最小白】变分自编码器 VAE:从降维本质,到自编码器,再到变分自编码器
?
降维本质:寻找隐空间和隐变量
机器学习就是想从数据中找到规律。
当数据维度很多的时候,会考虑降维。
先看俩个概念:隐空间、隐变量。

降维通常是为了发现数据的简化表示,其中包括寻找隐空间和隐变量的过程。
降维的过程就像是从这堆照片中提取关键信息,比如人脸的形状、眼睛的大小、嘴巴的宽度等,而不是关注每一个像素点。
这个简化的表示就是隐空间,而提取出来的关键特征就是隐变量。
通过降维,我们能够找到更低维度的空间,这个空间尽量保留了原始数据的重要信息。
对数据分析非常有用,因为在较低维度的空间中处理数据通常更高效,有助于揭示数据的内在结构和模式,减少噪声、冗余信息。
?
自编码器:论降维,PCA纯线性不及我深邃,编码器-解码器不及我牛逼
PCA是线性降维的,无法捕捉到数据中的非线性结构。
编码器-解码器、自编码器都是深度非线性的,可以通过增加网络层数和调整网络结构来捕获数据中的复杂模式和关系。
当然,自编码器降维能力更强。
自编码器结构图:

自编码器的降维能力源自它的隐藏层通常比输入层和输出层的维度要小,因此自编码器被迫学习输入数据中最重要的特征。
编码器-解码器模型并不是专门为降维设计的。它们是为了处理序列到序列的转换问题,例如机器翻译。
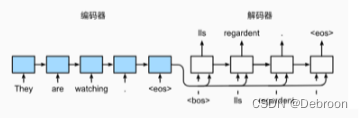
无损重建
自编码器结构,编码器抓主要特征,解码器重建原始特征。
是通过最小化输入数据、解码器数据之间的重构误差来更新参数的。
但这也导致了自编码器的问题。
- 如果没有任何先验知识,自编码器降维分类有缺陷。
镜像一个制陶艺人,目标是用一堆黏土(输入数据)塑造出一个尽可能接近原始黏土块(原始输入)的作品(重建输出)。但是,如果你要求这位艺人盲目地塑造作品,而不提供任何关于黏土最终应该呈现什么形状或风格的先验知识。
那收到的是一个整体形状相同,但细微纹理或图案不是你想要的。
- 因为自编码器以最小损失为目标,不会管隐空间如何组织,会严重过拟合。
无损重建的隐空间:
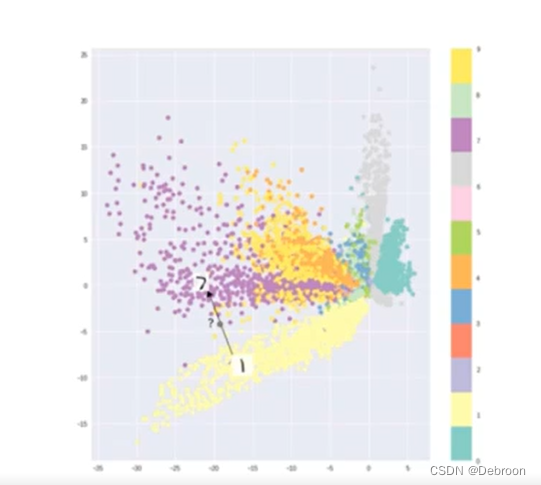
虽然能分出类别,但数据分布不均匀。
数据之间存在大量地方空白,如果用这些地方生成数据,那啥也不是。
?
变分自编码器 VAE:解决自编码器的过拟合问题
变分自编码器:
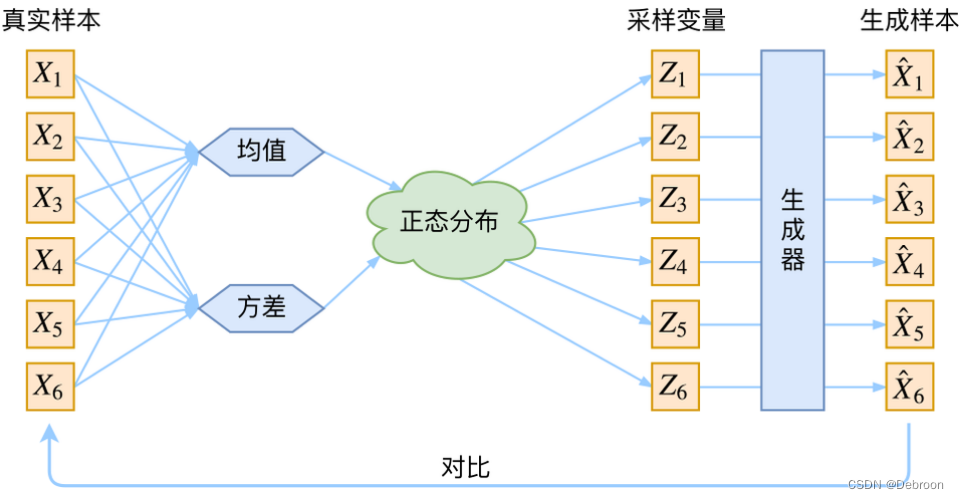
变分自编码器,是从隐空间随机采样给生成目的的解码器,必须保证隐空间足够规则,避免过拟合。
如果模型非常复杂,可能会过分地拟合训练数据中的每一个小细节,包括噪声。
引入正则化:从求最大似然函数 MLE,改成最大后验估计 MAP
为了防止过拟合,我们可以使用正则化。
正则化,通过在模型的损失函数中加入一个额外的项(正则项),来惩罚模型的复杂度。
这个正则项就是在告诉模型:“在尽可能准确地拟合数据的同时,请尽量保持简单。”
引入正则化,让模型不在把输入数据当成隐空间中的单个点(固定编码值),而是隐空间的概率分布:

类似扔飞镖,目标是射中飞镖靶心。
在没有正则化的情况下,你每次射中的地方都是靶上的一个特定点。
但你扔过就知道,你不可能每次都射中同一个点一样,由于手的抖动或者风的影响、力度、食指的摆放位置、身体的姿态等,你射出的每一支飞镖并不总是落在同一个点上,而是在靶心周围形成了一个分布区域。
抓住数据的本质特征,每个输入数据点都可以有多种可能的表示形式,而不是只有一种,而不是只拟合到特定的样本点,从而增强对新样本的适应能力。
在机器学习中,使用正则化就像是在你的判断中加入先验知识。
假设你要解决一个案件,案发现场有很多线索(数据),你需要找出最有可能的犯罪嫌疑人(模型参数)。
最大似然估计 MLE 就像是你仅仅基于现场的线索来判断谁是犯人。
你会看哪个嫌疑人与现场线索匹配得最好,就认为他可能就是犯人。
- 最大化似然函数,就是找到一组参数,使得观察到的数据出现的概率最大。
先验就好比你在案件发生之前就已经知道的关于犯罪嫌疑人的一些信息。
比如,你知道被害人和歹徒搏斗的过程中,在歹徒肩膀上划了一道伤口。这些信息就是你的“先验”知识。
最大后验估计 MAP 就是你不仅考虑案发现场的线索,还要结合你的先验知识来判断犯人。
换句话说,你不仅看线索与哪个嫌疑人匹配,还会考虑这个嫌疑人肩膀上有没有伤口。
- 最大化后验概率,就是结合了先验信息后,寻找使得数据和先验知识共同出现概率最大的参数。
引入正则化后,自编码器隐空间:
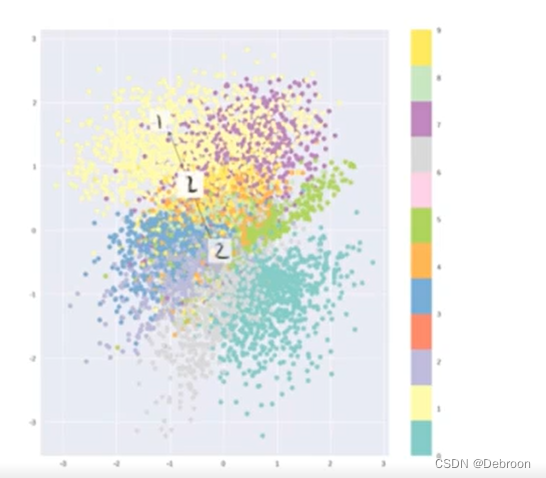
数据分布均匀、还能分出类别。
?
变分推理
变分自编码器具体结构:
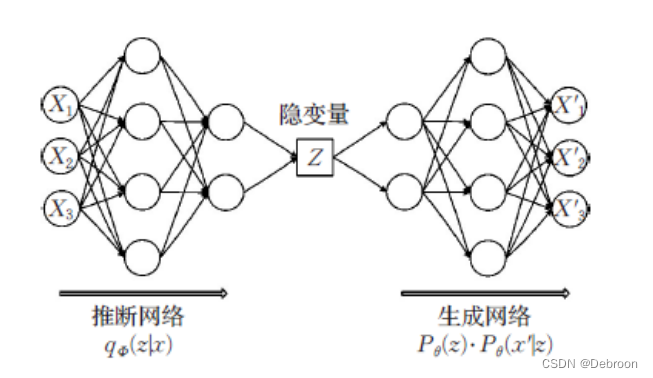
输入数据 x 是由隐变量 z 生成:
q ? ( ? z ∣ ? x ) = q ? ( ? x ∣ z ) ? q ? ( ? z ) q ? ( ? x ? ) q~(~z|~x)=\frac{q~(~x\mid z)~q~(~z)}{q~(~x~)} q?(?z∣?x)=q?(?x?)q?(?x∣z)?q?(?z)?
x 可观测,正则化是 q ( x ) q(x) q(x),z 不可观测。
可以通过 x 反推 z:
q ( x ) = ∫ q ( x ∣ z ) q ( z ) d z q(x)=\int q(x|z)q(z)dz q(x)=∫q(x∣z)q(z)dz
可这个不好算,没有解析解。
但我们可以用变分推断来算。
数学公式:
(
g
?
,
h
?
)
=
arg
?
min
?
?
(
a
.
h
)
∈
G
×
H
K
L
(
q
x
(
z
)
,
p
(
z
∣
x
)
)
=
arg
?
min
?
(
g
,
h
)
∈
G
×
H
(
E
z
~
q
x
(
log
?
q
x
(
z
)
)
?
E
z
~
q
x
(
log
?
p
(
x
∣
z
)
p
(
z
)
p
(
x
)
)
)
=
arg
?
min
?
(
g
,
h
)
∈
G
×
H
(
E
z
~
q
x
(
log
?
q
x
(
z
)
)
?
E
z
~
q
x
(
log
?
p
(
z
)
)
?
E
z
~
q
x
(
log
?
p
(
x
∣
z
)
)
+
E
z
~
q
x
(
log
?
p
(
x
)
)
)
=
arg
?
max
?
?
(
g
,
h
)
∈
G
×
H
(
E
z
~
q
x
(
log
?
p
(
x
∣
z
)
)
?
K
L
(
q
x
(
z
)
,
p
(
z
)
)
)
=
arg
?
max
?
(
g
,
h
)
∈
G
×
H
(
E
z
~
q
x
(
?
∣
∣
x
?
f
(
z
)
∣
∣
2
2
c
)
?
K
L
(
q
x
(
z
)
,
p
(
z
)
)
)
\begin{aligned} (g^{*},h^{*})& =\underset{(a.h)\in G\times H}{\operatorname*{\arg\min}}KL(q_x(z),p(z|x)) \\ &=\arg\min_{(g,h)\in G\times H}\left(\mathbb{E}_{z\sim q_x}(\log q_x(z))-\mathbb{E}_{z\sim q_x}\left(\log\frac{p(x|z)p(z)}{p(x)}\right)\right) \\ &\begin{aligned}&=\arg\min_{(g,h)\in G\times H}(\mathbb{E}_{z\sim q_x}(\log q_x(z))-\mathbb{E}_{z\sim q_x}(\log p(z))-\mathbb{E}_{z\sim q_x}(\log p(x|z))+\mathbb{E}_{z\sim q_x}(\log p(x)))\end{aligned} \\ &=\underset{(g,h)\in G\times H}{\operatorname*{\arg\max}}(\mathbb{E}_{z\sim q_x}(\log p(x|z))-KL(q_x(z),p(z))) \\ &=\arg\max_{(g,h)\in G\times H}\left(\mathbb{E}_{z\sim q_x}\left(-\frac{||x-f(z)||^2}{2c}\right)-KL(q_x(z),p(z))\right) \end{aligned}
(g?,h?)?=(a.h)∈G×Hargmin?KL(qx?(z),p(z∣x))=arg(g,h)∈G×Hmin?(Ez~qx??(logqx?(z))?Ez~qx??(logp(x)p(x∣z)p(z)?))?=arg(g,h)∈G×Hmin?(Ez~qx??(logqx?(z))?Ez~qx??(logp(z))?Ez~qx??(logp(x∣z))+Ez~qx??(logp(x)))?=(g,h)∈G×Hargmax?(Ez~qx??(logp(x∣z))?KL(qx?(z),p(z)))=arg(g,h)∈G×Hmax?(Ez~qx??(?2c∣∣x?f(z)∣∣2?)?KL(qx?(z),p(z)))?
第一行,就是近似俩个分布:
- q ( z ∣ x ) q(z|x) q(z∣x) 是高斯分布,先验知识
- p ( z ∣ x ) p(z|x) p(z∣x) 是真实分布
- 目标是找到一对函数 ( g , h ) (g, h) (g,h)(高斯分布的均值和方差)
- 通过迭代 ( g , h ) (g, h) (g,h),当俩个分布越接近,那我们最终就会知道 真实的分布 了
第二行,把KL按定义展开,变成期望形式。
第三行,分解交叉熵。
第四行,最小化 KL 散度等价于最大化 l o g p ( x ∣ z ) log p(x|z) logp(x∣z) 的期望值减去 q x ( z ) q_x(z) qx?(z) 和 p ( z ) p(z) p(z) 之间的 KL 散度。
第五行,假设 p ( x ∣ z ) p(x|z) p(x∣z)遵循高斯分布,可以将 l o g p ( x ∣ z ) log p(x|z) logp(x∣z)的期望值写为 ? ∣ ∣ x ? f ( z ) ∣ ∣ 2 2 c -\frac{||x-f(z)||^2}{2c} ?2c∣∣x?f(z)∣∣2?的形式
总结起来,我们要找的函数对 ( g , h ) (g, h) (g,h) 应当最大化对数似然项(数据 x x x 给定 z z z 的概率)的期望。
并同时最小化潜在变量 z z z 的分布 q x ( z ) q_x(z) qx?(z) 与其先验 p ( z ) p(z) p(z) 之间的KL散度。
这样做能够使得我们的模型既能够精确地重构数据 x x x,又能够保证潜在空间 z z z 有好的结构性质。
损失函数 = 无损重建 + 正则化
( f ? , g ? , h ? ) = arg ? max ? ( f , g , h ) ∈ F × G × H ( E z ~ q x ( ? ∣ ∣ x ? f ( z ) ∣ ∣ 2 2 c ? K L ( q x ( z ) , p ( z ) ) ) ) (f^*,g^*,h^*)=\arg\max_{(f,g,h)\in F\times G\times H}(\mathbb{E}_{z\sim q_x}(-\frac{||x-f(z)||^2}{2c}-KL(q_x(z),p(z)))) (f?,g?,h?)=argmax(f,g,h)∈F×G×H?(Ez~qx??(?2c∣∣x?f(z)∣∣2??KL(qx?(z),p(z))))
最优化 f 、 g 、 h f、g、h f、g、h,这组函数能够在最大化数据 x x x 的重构质量(最小化重构误差)的同时,使得编码器输出的概率分布接近于先验分布。
f 、 g 、 h f、g、h f、g、h 分别来自解码器、编码器和一个辅助函数,就是他们 3 者的最佳组合。
这个公式分为俩部分:
- 无损重建 ? ∣ ∣ x ? f ( z ) ∣ ∣ 2 2 c -\frac{||x-f(z)||^2}{2c} ?2c∣∣x?f(z)∣∣2?
- 正则化 ? K L ( q x ( z ) , p ( z ) ) -KL(q_x(z), p(z)) ?KL(qx?(z),p(z))
- c c c 是俩者的调节系数,越大,正则化权重越大
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!