Python实现的有向图结构的示例
2023-12-15 00:27:13
一、图数据结构的概念:
????????图是非线性的数据结构,图是由顶点和边组成的。如果图中的顶点是有序的,那么图是有方向的,称之为有向图,如下图 所示;否则,图是无方向的,称之为无向图。在图中,由顶点组成的序列称之为路径。图和树相比,少了树那样明显的层次结构。
??????? 在 Python 中,可以采用字典的方式来创建图,图中的每个元素都是字典中的键,该元素所指
向的图中其他元素组成键的值。
????????与树一样,对于图来说,也可以对其进行遍历。除了遍历以外,还可以在图中搜索所有的从一个顶点到另一个顶点的路径。
????????图中的每一顶点可以看作一个城市,路径可以看作城市到城市之间的公路。因此,通过搜索所有的路径,可以找到一个顶点到另一个顶点的最短路径,即城市到城市间的最短路线。
二、示例代码对应的有向图结构:
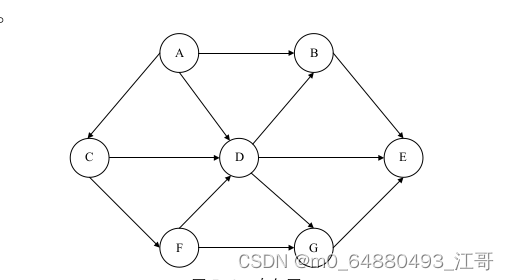
三、示例代码:
def searchGraph(graph, start, end): # 搜索树的函数
results = []
generatePath(graph, [start], end, results) # 生成路径
results.sort(key=lambda x: len(x)) # 按照路径长短排序
return results
def generatePath(graph, path, end, results): # 生成路径的函数
state = path[-1]
if state == end:
results.append(path)
else:
for arc in graph[state]:
generatePath(graph, path + [arc], end, results)
if __name__ == '__main__':
Graph = {'A': ['B', 'C', 'D'], # 构建图
'B': ['E'],
'C': ['D', 'F'],
'D': ['B', 'E', 'G'],
'E': [],
'F': ['D', 'G'],
'G': ['E']
}
r = searchGraph(Graph, 'A', 'D') # 搜索A到D的所有路径
print('path A to D:')
for i in r:
print(i)
r = searchGraph(Graph, 'C', 'E') # 搜索C到E的所有路径
print('path C to E:')
for i in r:
print(i)
四、运行结果:
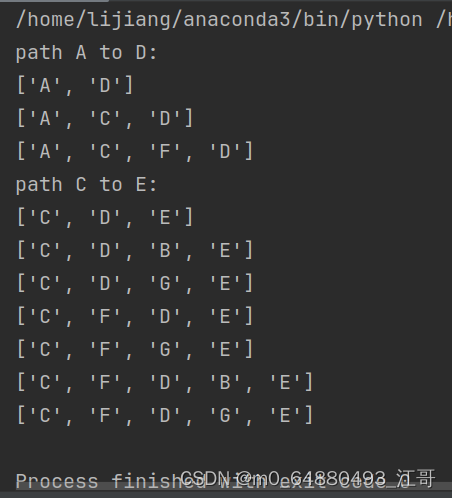
文章来源:https://blog.csdn.net/m0_64880493/article/details/134931592
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!