交通 | DRL4LRP:空间优化之经典问题新方法
论文原文:Wang, S., Zhou, J., Liang, H., Wang, Z., Su, C., & Li, X. (2023, November). A New Approach for Solving Location Routing Problems with Deep Reinforcement Learning of Emergency Medical Facility. In Proceedings of the 8th ACM SIGSPATIAL International Workshop on Security Response using GIS 2023 (pp. 50-53).https://doi.org/10.1145/3615884.3629429
推文作者:周俊源(兰州交通大学),梁浩健(吉林大学),王少华(中国科学院空天信息创新研究院)
选址-路径问题(Location-Routing Problem, LRP)在应急医疗设施(Emergency Medical Facility)等选址优化中具有广泛应用。LRP是一个复杂的空间优化问题,即从一组需求点和候选设施位置中选择最佳设施位置并规划高效路线。本研究提出了一种基于深度强化学习的两阶段方法,充分发挥了深度强化学习在处理序贯决策问题方面的潜力。首先,在选址优化阶段,通过智能体与环境之间的交互,智能体需要从众多需求点中选择设施位置,以最大化总体利润或最小化总体成本。该阶段确定中心点并将需求点分配到最近的设施位置。随后,在路径规划阶段,代理决定如何在预先选择的设施位置之间分配交货,以最大限度地减少总体路线长度或成本。
实验结果表明该方法解决LRP的有效性。该方法可为应对应急事件提供重要的方法支持,辅助决策者对设施位置和路线规划做出优化选择,进而提高服务响应速度和效率。此外,该方法在可持续城市发展领域具有广泛的应用潜力,有助于推动深度强化学习在空间优化问题中的发展。
1. 背景
随着运输能力的不断提高,日益增多的需求对物流管理提出了很多要求,设施选址和路径规划是重要的研究问题。科学合理的设施选址和路径规划有利于提高整个物流系统的效率,同时降低成本。为了满足各种物流系统的不同需求,设施选址和路径规划等涌现出了众多创新研究。
当前,突发自然灾害、公共卫生应急等时有发生。如何合理选择应急物流中心位置,快速安全地将应急物资等精准运送到需求点,并更好地控制总成本是应急服务的核心问题。耦合地理空间特征、空间优化模型和前沿深度学习技术,引入创新的视角,成为研究选址优化问题领域的新研究方向 [1-3]。
[1] Church R L, Wang S. Solving the p-median problem on regular and lattice networks [J]. Computers & Operations Research, 2020, 123: 105057.
[2] Liang H, Wang S, Li H, et al. A Trade-Off Algorithm for Solving p-Center Problems with a Graph Convolutional Network [J]. ISPRS International Journal of Geo-Information, 2022, 11(5): 270. https://doi.org/10.3390/ijgi11050270
[3] Wang S, Liang H, Zhong Y, et al. DeepMCLP: Solving the MCLP with Deep Reinforcement Learning for Urban Facility Location Analytics. SDSS 2023.
https://doi.org/10.25436/E2KK5V
LRP包括设施选址问题(Facility Location Problem, FLP)和车辆路径问题(Vehicle Routing Problem, VRP),前者设施优化的结果对后者的效率有一定的影响,而后者的效率又反过来影响设施优化决策的整体效果,二者相辅相成,因此若将两者分开决策,则无法产生最优结果。Salhi, S. 和 Rand, G. K. [4] 已经证明通过将LRP分解为FLP和VRP并依次解决这些问题来解决LRP的策略并非最优。
Cooper [5] 在Operations Research上发表文章,将FLP和VRP结合,提出LRP问题。一方面,随着交通物流领域的发展和在实践中的重要作用,LRP日益成为运筹优化领域研究的热点,衍生了诸多改进的数学模型。另一方面,由于FLP和VRP问题均涉及复杂的问题因素且具有动态变化的问题特征,在进行相关问题模型求解时相对困难。因此,学者们设计了门类繁多的运筹优化算法进行求解,大致可分为精确算法 [6-8] 和启发式算法 [9] 两类。
随着人工智能技术的兴起,以及深度强化学习在求解组合优化问题(Machine Learning for Combinatorial Optimization, ML4CO)[10] 取得的成功,本文作者尝试用新方法求解经典的LRP,以期提高服务响应速度和效率,并推动深度强化学习在空间优化问题中的发展。
2. LRP模型构建
LRP作为一个经典的运筹优化问题,面向交通物流领域,考虑一组潜在设施和一组客户。LRP的主要决策包括:(1)开放设施的数量和位置;(2)已开放设施的客户分配;(3)设计使用车队为每个设施的客户提供服务的路线。
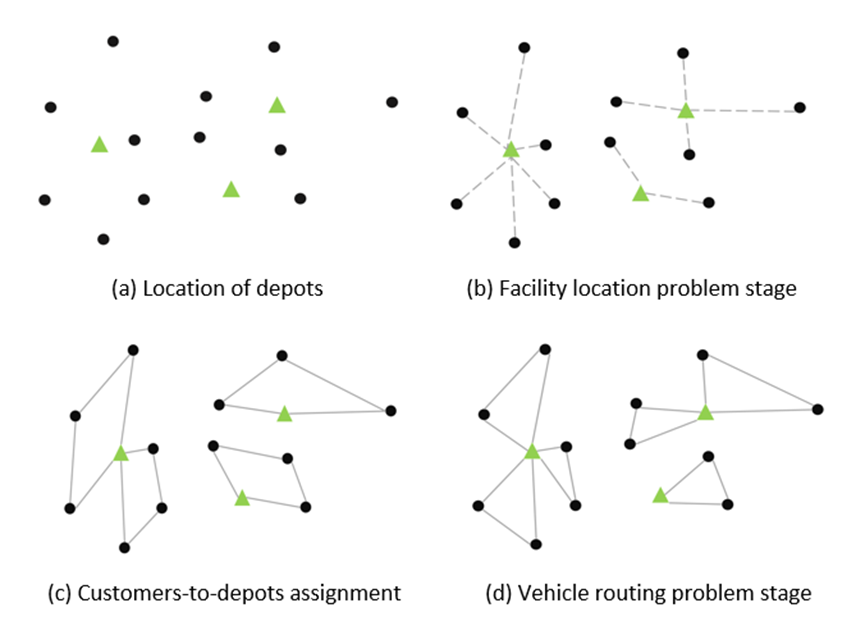
图1 LRP问题示例
符号说明: V V V代表节点的集合, V = I ∪ J V=I\cup J V=I∪J, I I I代表潜在仓库节点的集合, J J J代表客户节点的集合, E E E代表边的集合, K K K代表车辆的集合, O i O_i Oi?代表固定打开仓库节点i的成本, Q i Q_i Qi?代表节点i的库容量, D j D_j Dj?代表客户对节点i的要求, q q q代表每辆车的装载能力, F F F表示车辆固定成本, c i j c_{ij} cij?代表边缘处的旅行成本 ( i , j ) \left(i,j\right) (i,j) , d d d代表每辆车允许的最大距离, U i U_i Ui?代表任何实数。
决策变量包括:
x
i
j
k
=
{
?
1
,
i
f
?
V
e
h
i
c
l
e
?
k
?
c
o
v
e
r
e
d
?
t
h
e
?
e
d
g
e
?
(
i
,
j
)
?
0
,
o
t
h
e
r
w
i
s
e
x_{ijk}= \begin{cases} \ 1,if\ Vehicle\ k\ covered\ the\ edge\ \left(i,j\right)\\ \ 0,otherwise \end{cases}
xijk?={?1,if?Vehicle?k?covered?the?edge?(i,j)?0,otherwise?
y
i
=
{
?
1
,
i
f
?
t
h
e
?
d
e
p
o
t
?
l
o
c
a
t
e
d
?
i
n
?
n
o
d
e
?
i
?
0
,
o
t
h
e
r
w
i
s
e
y_i= \begin{cases} \ 1,if\ the\ depot\ located\ in\ node\ i\\ \ 0,otherwise \end{cases}
yi?={?1,if?the?depot?located?in?node?i?0,otherwise?
z
i
j
=
{
?
1
,
i
f
?
c
u
s
t
o
m
e
r
?
j
?
i
s
?
s
e
r
v
i
c
e
d
?
b
y
?
d
e
p
o
t
?
i
?
0
,
o
t
h
e
r
w
i
s
e
z_{ij}= \begin{cases} \ 1,if\ customer\ j\ is\ serviced\ by\ depot\ i\\ \ 0,otherwise \end{cases}
zij?={?1,if?customer?j?is?serviced?by?depot?i?0,otherwise?
LRP的MILP混合整数线性规划(Mixed-Integer Linear Programming)公式如下:
m
i
n
???
∑
i
∈
I
O
i
y
i
+
∑
i
∈
V
∑
j
∈
V
∑
k
∈
K
c
i
j
x
i
j
k
+
∑
i
∈
I
∑
j
∈
J
∑
k
∈
K
F
x
i
j
k
\begin{equation} \\min{\ \ \ }\sum_{i\in I} O_iy_i+\sum_{i\in V}\sum_{j\in V}\sum_{k\in K} c_{ij}x_{ijk}+\sum_{i\in I}\sum_{j\in J}\sum_{k\in K} F x_{ijk} \end{equation}
min???i∈I∑?Oi?yi?+i∈V∑?j∈V∑?k∈K∑?cij?xijk?+i∈I∑?j∈J∑?k∈K∑?Fxijk???
∑
i
∈
V
∑
k
∈
K
x
i
j
k
=
1
???
?
j
∈
J
\begin{equation} \sum_{i\in V}\sum_{k\in K} x_{ijk}=1\ \ \ \forall j\in J \end{equation}
i∈V∑?k∈K∑?xijk?=1????j∈J??
∑
i
∈
I
∑
j
∈
J
x
i
j
k
≤
1
???
?
k
∈
K
\begin{equation} \sum_{i\in I}\sum_{j\in J} x_{ijk}\le1\ \ \ \forall k\in K \end{equation}
i∈I∑?j∈J∑?xijk?≤1????k∈K??
∑
j
∈
V
x
i
j
k
?
∑
j
∈
V
x
j
i
k
=
0
???
?
k
∈
K
,
???
?
i
∈
V
\begin{equation} \sum_{j\in V} x_{ijk}-\sum_{j\in V} x_{jik}=0\ \ \ \forall k\in K,\ \ \ \forall i\in V \end{equation}
j∈V∑?xijk??j∈V∑?xjik?=0????k∈K,????i∈V??
U
i
?
U
j
+
(
n
?
1
)
x
i
j
k
≤
n
?
2
???
?
i
∈
J
,
???
?
j
∈
J
,
i
≠
j
???
?
k
∈
K
\begin{equation} U_i-U_j+\left(n-1\right)x_{ijk}\le n-2\ \ \ \forall i\in J,\ \ \ \forall j\in J,i\neq j\ \ \ \forall k\in K \end{equation}
Ui??Uj?+(n?1)xijk?≤n?2????i∈J,????j∈J,i=j????k∈K??
∑
u
∈
J
x
i
u
k
+
∑
u
∈
V
j
x
u
j
k
≤
1
+
z
i
j
???
?
i
∈
I
,
???
?
j
∈
J
,
???
?
k
∈
K
\begin{equation} \sum_{u\in J} x_{iuk}+\sum_{u\in V{j}} x_{ujk}\le1+z_{ij}\ \ \ \forall i\in I,\ \ \ \forall j\in J,\ \ \ \forall k\in K \end{equation}
u∈J∑?xiuk?+u∈Vj∑?xujk?≤1+zij?????i∈I,????j∈J,????k∈K??
s
.
t
.
∑
i
∈
V
∑
j
∈
J
D
j
x
i
j
k
≤
q
???
?
k
∈
K
\begin{equation} s.t. \sum_{i\in V}\sum_{j\in J} D_jx_{ijk}\le q\ \ \ \forall k\in K \end{equation}
s.t.i∈V∑?j∈J∑?Dj?xijk?≤q????k∈K??
∑
j
∈
J
D
j
z
i
j
≤
Q
i
y
i
???
?
i
∈
I
\begin{equation} \sum_{j\in J} D_jz_{ij}\le Q_iy_i\ \ \ \forall i\in I \end{equation}
j∈J∑?Dj?zij?≤Qi?yi?????i∈I??
∑
i
∈
V
∑
j
∈
V
c
i
j
x
i
j
k
≤
d
?
k
∈
K
\begin{equation} \sum_{i\in V}\sum_{j\in V} c_{ij}x_{ijk}\le d ?k∈K \end{equation}
i∈V∑?j∈V∑?cij?xijk?≤d?k∈K??
∑
i
∈
l
∑
j
∈
j
∑
k
∈
K
x
i
j
k
≤
∣
K
∣
\begin{equation} \sum_{i\in l}\sum_{j\in j}\sum_{k\in K} x_{ijk}\le \left|K\right| \end{equation}
i∈l∑?j∈j∑?k∈K∑?xijk?≤∣K∣??
x
i
j
k
∈
{
0
,
1
}
??
?
i
∈
V
,
???
?
j
∈
V
,
???
?
k
∈
K
\begin{equation} x_{ijk}\in\left\{0,1\right\}\ \ \forall i\in V,\ \ \ \forall j\in V,\ \ \ \forall k\in K \end{equation}
xijk?∈{0,1}???i∈V,????j∈V,????k∈K??
y
i
∈
{
0
,
1
}
??
?
i
∈
I
\begin{equation} y_i\in\left\{0,1\right\}\ \ \forall i\in I \end{equation}
yi?∈{0,1}???i∈I??
z
i
j
∈
{
0
,
1
}
??
?
i
∈
I
,
???
?
j
∈
V
\begin{equation} z_{ij}\in\left\{0,1\right\}\ \ \forall i\in I,\ \ \ \forall j\in V \end{equation}
zij?∈{0,1}???i∈I,????j∈V??
U
i
∈
R
???
?
i
∈
J
\begin{equation} U_i\in R\ \ \ \forall i\in J \end{equation}
Ui?∈R????i∈J??
其中,目标函数(1)旨在最小化总成本,其中包括仓库的开设成本、车辆的可变距离成本和车辆的固定使用成本。约束 (2) 确保每个客户只能由一辆车访问,保障执行路线约束。约束(3)确保所有路线从仓库开始和结束,而约束(4)是连接性约束,以确保每辆车在服务后离开每个客户。子旅程消除约束由约束(5)定义。约束 (6) 确保只有存在到某个仓库的路线时才能将客户分配到该仓库。约束条件(7)和(8)分别规定每辆车的容量和每个仓库的容量不得超过。约束(9)确保每辆车的路线长度不超过最大距离约束。约束(10)限制了使用的车辆数量。约束(11)至(14)定义了决策变量。
3. 深度强化学习DRL4LRP
在LRP中,有两个主要问题需要解决:FLP和VRP,这两个问题都可以建模为序贯决策过程(Sequential decision process)。在本节中,我们提出了一种基于深度强化学习(DRL)的两阶段算法来解决应急设施LRP,包括设施选址问题阶段和路径规划阶段。在选址问题和路径问题中,节点分为三类:需求点、物流中心和配送中心。
3.1 选址问题阶段
在设施选址选择阶段,我们将问题建模为马尔可夫决策过程(Markov Decision Process, MDP)。智能代理需要从所有需求点中选择一个或多个位置来建设设施,旨在最大化总收入或最小化总成本。为实现这一目标,我们遵循以下步骤:
- 状态:定义状态表示,其中包括当前选择的设施位置、需求点状态以及其他相关信息;
- 动作:定义一个动作空间,代理可在其中选择构建设施的位置;
- 奖励:设计奖励函数,以便代理可根据所选位置接收适当的奖励信号。奖励可以考虑成本、收入和需求满足程度等因素。
综上,设施的部署随选址阶段的完成,选址点被遴选为视为中心点,每个需求点分配给最近的设施点。
3.2 路径规划阶段
在路径规划阶段,路径问题也可建模为MDP。在此阶段,智能代理需要决定如何在选定的设施位置之间分配递送,以最大限度地减少总体路径长度或成本。
两阶段算法的求解框架如下图2所示:
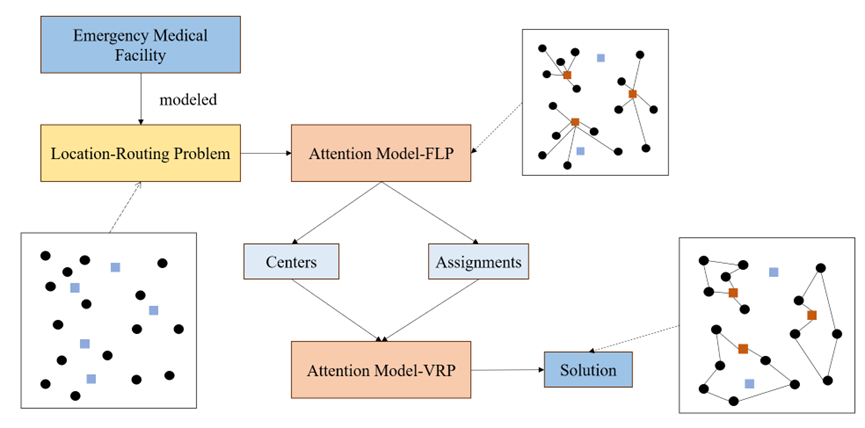
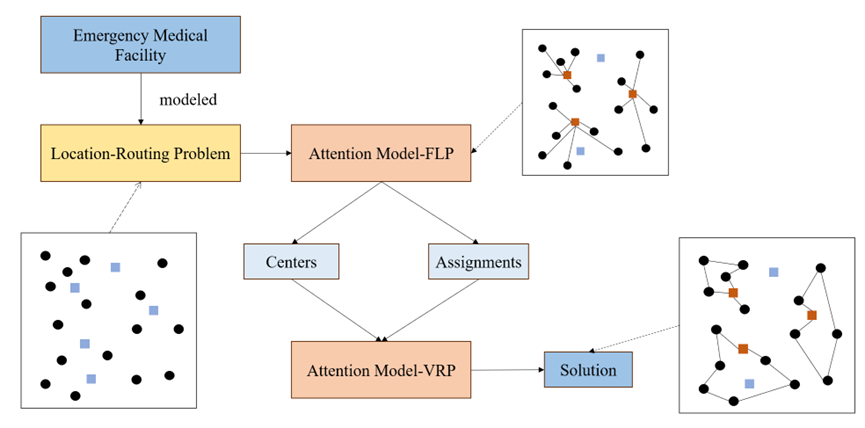
图2 应急医疗设施LRP的两阶段算法结构
应急医疗设施LRP解决方式主要分两步,即实现需求点与设施点的多对一分配,以及分配后的路径规划问题。首先需要将需求点以及备选设施点的位置信息等进行存入,结合选址-路径模型进行分析。第一步是将属性信息导入到AM-FLP(Attention Model-Facility Location Problem)模型中,从众多备选设施点中选出位于众多需求点中心的点位作为设施点,接着将众多需求点分配给所选设施点。第二步是将所选设施点以及对应需求点的分配结果输入到AM-VRP(Attention Model-Vehicle Routing Problem)模型中,以各设施点为重心,对途径各需求点的路径进行规划,最后输出符合需求的设施点信息以及路径。
3.3 深度强化学习算法
我们采用深度强化学习算法REINFORCE来训练我们的AM-FLP和AM-VRP,该算法是一种梯度策略方法,其算法步骤如下:
- 定义一个策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s),用来描述给定状态 s s s下采取动作 a a a的概率分布,本文用 π F L P ( a ∣ s ) \pi_{FLP}(a|s) πFLP?(a∣s)和 π V R P ( a ∣ s ) \pi_{VRP}(a|s) πVRP?(a∣s)分别表示AM-FLP网络和AM-VRP网络;
- 通过策略函数,从环境中采样多个轨迹,并记录每个轨迹中的状态、动作,以及对应的奖励函数(目标函数是距离最小化或成本最小化,这里取目标函数的相反数);
- 对于每一个轨迹,计算累积回报。回报表示了在一次尝试中执行该策略的质量;
- 根据计算得到的梯度信息,使用梯度下降法,更新策略函数的参数,以使期望回报增加;
- 不断重复上述步骤,直到策略函数收敛到一个满足要求的策略,或者达到预定义的训练迭代次数。
4. 实验与分析
本文提出了一种基于深度强化学习的LRP求解新方法。对于LRP,我们构建了两种不同的注意力模型AM-FLP和AM-VRP,分别用于解决选址问题和路径问题。我们随机生成 2000 个实例来评估结果。每个示例由50个需求点组成,任务是从50个需求点中选择8个点作为中心点。然后,按照贪心方法,将剩余的需求点分配给最近的中心点,从而将所有节点分为 8 类。最后,对于每个类别,选择最短路径来遍历所有节点。实验结果如表1所示。N表示需求点的数量,p表示中心的数量。
表1 Gurobi vs. GA vs. AM在N=50, p=8上的位置路由问题的比较结果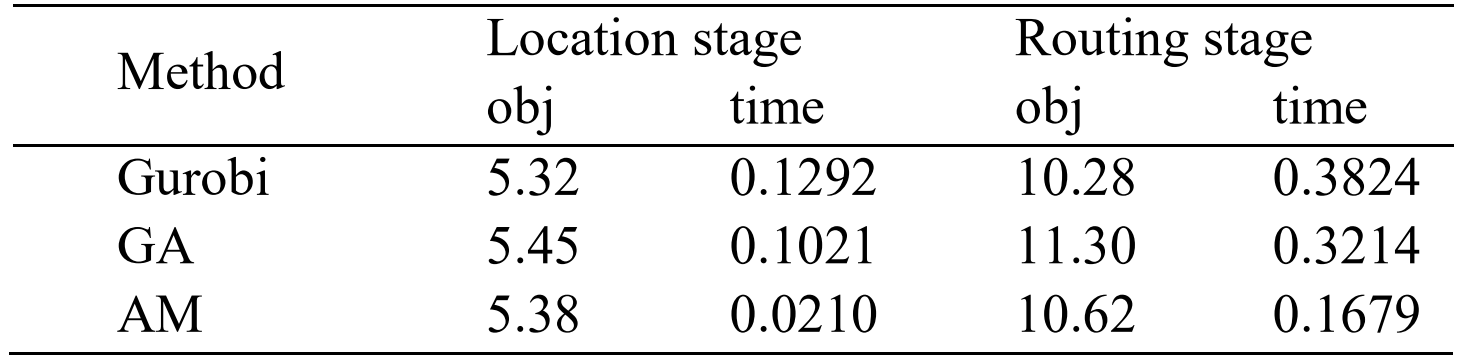
我们将应急设施LRP的解决分为两个阶段。表1从应急设施选址阶段和路径规划阶段的目标函数和求解时间方面说明了三种不同的方法。作为公认的最佳解决方案,求解器Gurobi在这个问题上表现得出色。即使在50个节点的情况下,它也能始终快速地获得最优解。另一方面,遗传算法(GA)作为一种启发式算法,与其他两种算法相比,其结果相对较差,基于GA算法结果的目标值与最优解之间的差距最大,这可能归因于遗传算法中的参数设置。本文提出采用深度强化学习(AM)方法求解应急设施选址路径问题,与遗传算法相比,与最优解的差距更小。此外,本文方法也是三种方法中算法求解时间最短。研究结果表明本文提出的方法在某种程度上实现了求解时间和准确性的平衡,使其成为一种应用潜力的创新方法。本文提出的方法可为解决应急设施LRP中解决时间和精度之间的权衡做出方法支撑。
本文研究相关的源代码和案例详细描述可参考课题组开源仓库:https://github.com/HIGISX/hispot
5. 总结与讨论
本文研究为应急医疗设施优化配置提供了一种新的、有效的方法,为实际应用带来了支撑,并为应对应急情况和自然灾害应急应对提供了有力支持和决策工具。未来研究将进一步探索该方法模型的泛化能力、挖掘空间特征在空间优化复杂问题求解的潜力及其在其他领域的应用,从而扩展其实际应用场景。
参考文献:
[1] Church R L, Wang S. Solving the p-median problem on regular and lattice networks [J]. Computers & Operations Research, 2020, 123: 105057.
[2] Liang H, Wang S, Li H, et al. A Trade-Off Algorithm for Solving p-Center Problems with a Graph Convolutional Network [J]. ISPRS International Journal of Geo-Information, 2022, 11(5): 270. https://doi.org/10.3390/ijgi11050270
[3] Wang S, Liang H, Zhong Y, et al. DeepMCLP: Solving the MCLP with Deep Reinforcement Learning for Urban Facility Location Analytics. SDSS 2023.
https://doi.org/10.25436/E2KK5V
[4] Salhi S, Rand G K. The effect of ignoring routes when locating depots[J]. European Journal of Operational Research, 1989, 39(2): 150-156.
[5] Cooper L. The transportation-location problem[J]. Operations Research, 1972, 20(1): 94-108.
[6] Laporte G, Nobert Y. An exact algorithm for minimizing routing and operating costs in depot location[J]. European Journal of Operational Research, 1981, 6(2): 224-226.
[7] Belenguer J M, Benavent E, Prins C, et al. A branch-and-cut method for the capacitated location-routing problem[J]. Computers & Operations Research, 2011, 38(6): 931-941.
[8] Contardo C, Cordeau J F, Gendron B. An exact algorithm based on cut-and-column generation for the capacitated location-routing problem[J]. INFORMS Journal on Computing, 2014, 26(1): 88-102.
[9] Schneider M, L?ffler M. Large composite neighborhoods for the capacitated location-routing problem[J]. Transportation Science, 2019, 53(1): 301-318.
[10] Bengio Y, Lodi A, Prouvost A. Machine learning for combinatorial optimization: a methodological tour d’horizon[J]. European Journal of Operational Research, 2021, 290(2): 405-421.
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!