27. 深度学习进阶 - 为什么RNN

Hi，你好。我是茶桁。

这节课开始，我们将会讲一个比较重要的一种神经网络，它对应了咱们整个生活中很多类型的一种问题结构，它就是咱们的RNN网络。

咱们首先回忆一下，上节课咱们学到了一些深度学习的一些进阶基础。

学了很多神经网络的Principles, 就是它的一些很重要的概念，比方层数维度。再然后咱们讲了Optimizer， 一些优化方式。还有weights的initialization，初始化等等。

那么大家具备了这些知识之后，那我们基本上已经能够解决常见的大概90%的机器学习问题了。

我们现实生活中绝大多数的机器学习问题，或者说识别问题都可以把它抽象成要么是分类，要么是回归问题。

一个柯基的例子

我们来一个例子，比方说一张图片里这个是什么动物，这显然是一个分类问题。

但是我们对这个图片的多个物体是什么，还有位置标注出来，那这个在里面前面会有一段是一个分类问题，后面还有一个长的向量，又会是一个回归问题。

我们只要知道分类和回归最大的区别就是一个返回的是一个类别，另外一个返回的是一个真正的数值。

那么接下来我们要正是的讲一下两种神经网络，RNN和CNN。这两个的目的是用来加速解决我们之前遇到的分类问题，或者回归问题。

在这些LSTM和CNN之类的高级的方法出现之前，其实我们用最直接的神经网络是可以解决所有的问题。

我们还是来看上面的那个例子，还是那张图片，如果要去分类看这图片里的是什么动物，我们把它形式化的表述一下。

假设我们这张图片现在是258*258的，那每一张图片进来之后，这个图片的饿背后其实都是一个向量：

# 258 * 258
from PIL import Image
import numpy as np

example_img = Image.open('assets/Corgi.png')
example_img = np.array(example_img)

print(example_img.shape)

---
(429, 696, 3)

我们可以看到这张图片在计算机里保存的时候是(429, 696, 3)这样的一组数字。

plt.imshow(example_img)

我们用plt展示出来，就是这样。

我们现在就可以讲整个图片变成一个向量，然后把它从立方体变的拉平：

example_img = example_img.reshape(1, -1)
print(example_img)

---
[[120 150  88 ...  43  39  38]]

那现在，我们要给这个图片做分类：

class Model(nn.Module):
    def __init__(self, input_dimension, categorical):
        super(Model, self).__init__()
        self.linear = nn.Linear(in_features=input_dimension, out_features=categorical)
        self.softmax = nn.Softmax()

    def forward(self, x):
        predict = self.softmax(self.linear(x))
        return predict
        ...

这里我们暂停一下，来说说这段代码中的super(...)，为了避免有些小伙伴Python基础不太好，这里说明一下。

如果有从我Python基础课就看过来的小伙伴，应该知道我在面向对象的时候应该是讲过这个方法。这个是为了在继承父类的时候，我们在重写父类方法的时候，依然可以调用父类方法。方式就是super().父类方法名()。有需要补Python基础的可以回头将我写的Python基础课程好好再看一遍。

好，我们继续回过头来讲，我们定义好这个Model之后，将图片数据变成一个PyTorch能够处理的一个example，当作训练数据传入train_x。

train_x = torch.from_numpy(example_img)
print('shape:{}, \ntrain_x:{}'.format(train_x.shape, train_x))

---
shape:torch.Size([1, 895752]), 
train_x:tensor([[120, 150,  88,  ...,  43,  39,  38]], dtype=torch.uint8)

然后进入线性函数，传入in_features为train_x.shape[1]， 把它变成一个10分类，再把test_model运行一下，将我们的train_x输入进去就可以了。

test_model = Model(input_dimension=train_x.shape[1], categorical=10)
output = test_model(train_x.float())

这样的话, 我们就可以产生出一个Softmax，有了这个Softmax，在这我们如果有很多个x，它就会对应我们很多个已知的y。

然后我们在这里定义一个loss：

criterion = torch.nn.CrossEntropyLoss()

再之后我们在做线性的时候之前，肯定是有一些ytrue数据的，肯定是知道它的y的，写个循环它就不断的可以去训练。

接着我们可以得到这个它的权重，那么在这里这是一张图片，如果这个图片要做回归，要给这个图片打分，那么将out_features换成1就可以了。

我们在Model里不断的去改它的东西，让它的输出能够满足就可以了。

不管是用户数据还是气象数据、天文数据、图片、文字，我们都可以把它变成这样的一个x向量。变成x向量之后只要送到一个模型里面，这个模型它能够去做优化，做些调整。那么它就能够去不断的去做优化。

当然，我们这里还缺一个optimizer：

optimizer = torch.optim.SGD(test_model.parameters(), lr=1e-3)

我们定义了一个SGD优化器，learning_rate设置了一下，给了一个初始的学习率。

然后呢再不断的去循环它就可以了：

# 定义虚拟的y
lable = np.random.randint(0,2,10)
train_y = torch.from_numpy(np.array([lable])).float()

for t in range(100):
    y_true = train_y
    y_predict = test_model(train_x.float())

    print(y_true.shape)
    print(y_predict.shape)

    print(loss)

我们现在可以将criterion假如到循环里来计算一下loss了。

for t in range(100):
    ...
    loss = criterion(y_predict, y_true)

就是说，我们之前学习的这些内容，不管是图片还是用户的数据、或者文字，其实都是可以变成一个向量，再把向量送入到定义好的模型里，求出它的结果。

再经过反复的运作，反复的调试来更新它的数据。

为什么RNN or CNN

那为什么我们还要学习RNN和CNN这些东西呢？我们刚开始学的wx+b的形式，可以把任意的x变成其它的一个output，
但是它在解决一些问题的时候效果就不是太好。

比方说啊，我们要识别一个图像到底是什么的时候，wx+b它是给每一个x一个权重, $w{x}_i+b$, 然后最后产出一个值。

但是图像我们是希望给中间一个区域一个平分，可是现在是一个点一个点的。

例如我们输入是一个x，输出是一个y。x它包含了多个x:{x1, x2, x3, …, xn}，那y的输出呢，它是和多个x有关系。如果是在一个曲线上，我们取几个点, {output1, output2, output3}, 那么这个output3就不止和${\vec{x}}_3$有关系，它和前面的output2, output1都有关系。

也就是说，当下这一时刻的数据其实不仅取不仅取决于今天发生的一些事情，还取决于昨天前天，甚至大前天发生的事情。

但是我们如果直接进行wxi+b的话，这里xi=x3，wx3+b我们期望输出一个output3，这样就忽略了前边的这些事情。

与此类似的还有我们写文章，当前这个字和前面是什么字应该是有依赖关系的。其实把它抽象一下的话，会发现在现实生活中其实有很多种依赖关系。

我们之前讲的wx+b，其实是一对一。

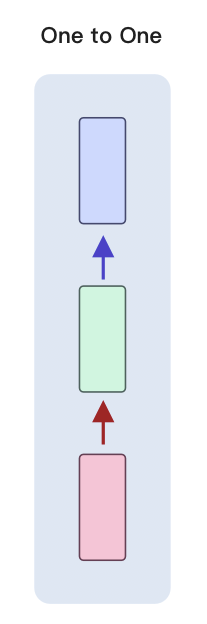
虽然x的维度可能会很大，y输出的维度也可能很大，但是它一个x就只对应输出一个y。

而除了one to one 之外，我们还有一些其他的类别：

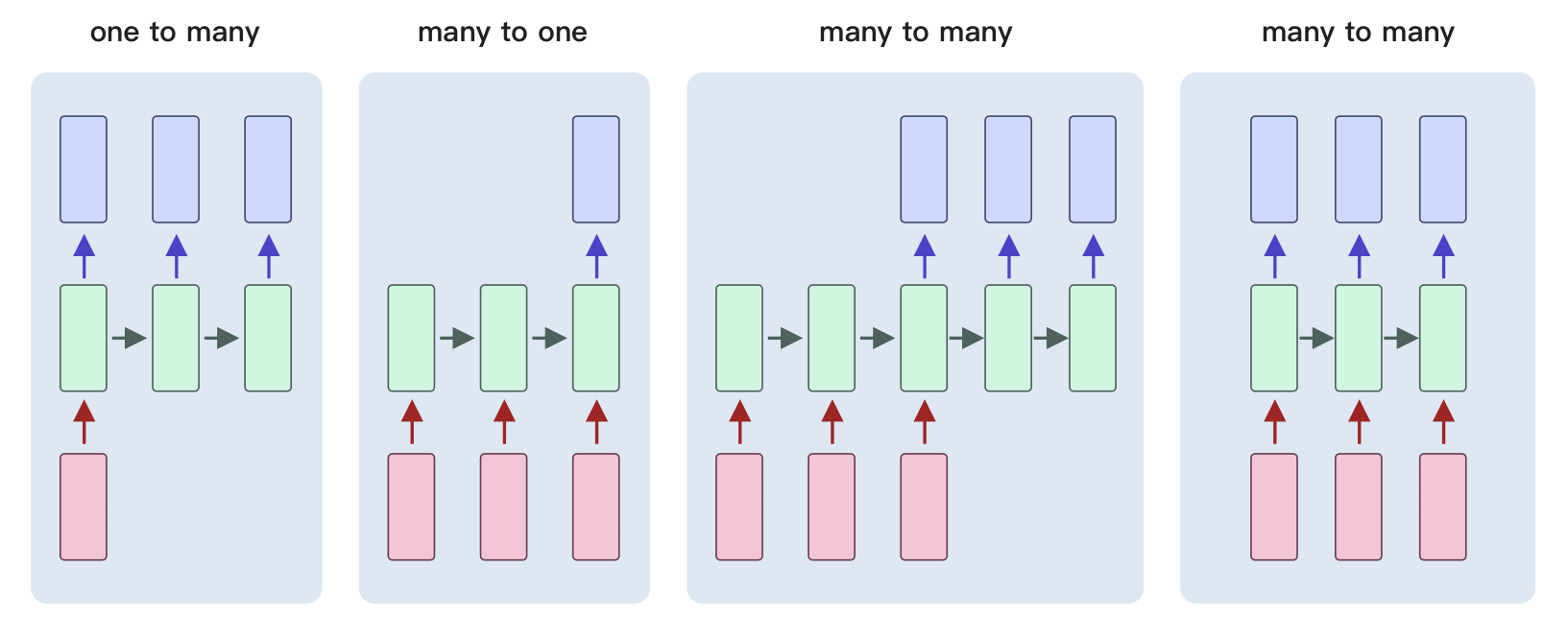
one to many，就是x输入之后，最后会输出多个y。比方说咱们输入的是一个类别，输出的是一篇文章，分别是第一个单词，第二个单词和第三个单词。

我们会发现，这三个输出的单词前后是有相关性的。这种就属于是一对多，输出的的这些内容是独立的个体，但是它们之间有相关性。

后面的many to one，典型的一个应用，你给他输入一句话，输出这个地方，这句话到底是表示正向的还是负向的。那么这句话其实每个单词之间是有依赖关系的，而输出的是一个值。

那many to many里，前边输入的这个input是一个序列，有依赖关系。输出也是一个序列，有依赖关系。那么这会是一个什么？比方我们的机器翻译，就有可能是这样一个关系，对吧？还有比方说我们会去做那个文本的阅读理解，文本的摘要。

那还有一个many to many和第一个有什么区别呢？它其实只是更加的实时，比如说同声传译。

对于这些所有的问题我们给它抽象一下，它每一步的输出就像我们之前学过递归函数一样，是和前一步的输出有关系，还和当前这一步的输入有关系, 我们其实学过最典型的一个依赖关系就是这样，就是斐波那契数列或者求阶乘：

def fib(n):
    if n == 0 or n == 1: return 1
    else:
        return fib(n-1) + fib(n-2)
    
def fac(n):
    if n == 0: return 1
    else: return n*fac(n-1)

for i in range(10): print('{}\t{}'.format(fib(i), fac(i)))

那么这个怎么实现的？我们要实现这个有多种方法，我们可以来看一个具体的案例：

class RNN(nn.Module):
    # implement RNN from scratch rather than ysubf nn.RNN
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()

        self.hidden_size = hidden_size
        self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
        self.i2o = nn.Linear(input_size + hidden_size, output_size)
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input_tensor, hidden_tensor):
        combined = torch.cat((input_tensor, hidden_tensor), 1)

        hidden = self.i2h(combined)
        output = self.i2o(combined)

这是一个非常经典的RNN的模型，我们来一起来分析它的构成。

在构造函数内，输入了一个input_size（x向量），还有一个hidden_size。然后在下面做了一个i2h的线性变化，这个线性变化它接受一个的两个参数， in_features是input_size + hidden_size, out_features是hidden_size。

现在有一个$\vec{x}$和一个$\vec{h}$， 将两个向量相加输入进入，然后会输出一个$vech$一样大小的东西。

然后下面还有一个i2o， 它是将input_size + hidden_size输入之后，输出一个output_size一样大小的东西。

在输出这两个之后，我们将output_size大小的这个向量，输入到Softmax里面，就会变成一个概率分布。

然后它继续forward的时候，继续向前运算的时候，它的输入是input和hidden，那它在这里，如果我们要求训练：

def train(line_tensor, category_tensor):
    hidden = rnn.init_hidden()

    for i in range(line_tensor.size()[0]):
        output, hidden = rnn(line_tensor[i], hidden)

这里它有很多的tensor，比如我们的x:[x1, x2, ..., xn], 这个tensor就是这些个x。那么它在做训练的第一步会取最前面的这个x向量，这个x向量刚开始会有一个随机的hidden向量，这个时候关键的地方就来了，就是它不断的重复:output, hidden = rnn(line_tensor[i], hidden), 我们来看，这个hidden就会一次一次的送进去做更新。

hidden一开始是随机的，之后t时刻的hidden的值是由上一时刻，也就是t-1时刻的x和hidden来影响的。

h0 -> random
(x0, h0) -> output1, h1
(x1, h1) -> output2, h2
...

这样，输出的output2不仅是x1的影响，也是受到x0的影响的，这样前后的关系就被连接起来了。

就比如说我们输入的是一段文字，就比说ChaHeng，输入C的时候，我们会得到一个hidden， 然后计算h时候，我们又会得到一个hidden, 一直到最后一个g，那我们算这一步的时候，它既包含了g这个字母， 还包含了之前n的hidden向量。那n再往上，一直到C都相关，这样它就实现了传递的效果。

那这个做法有两个人分别提出来了两种。

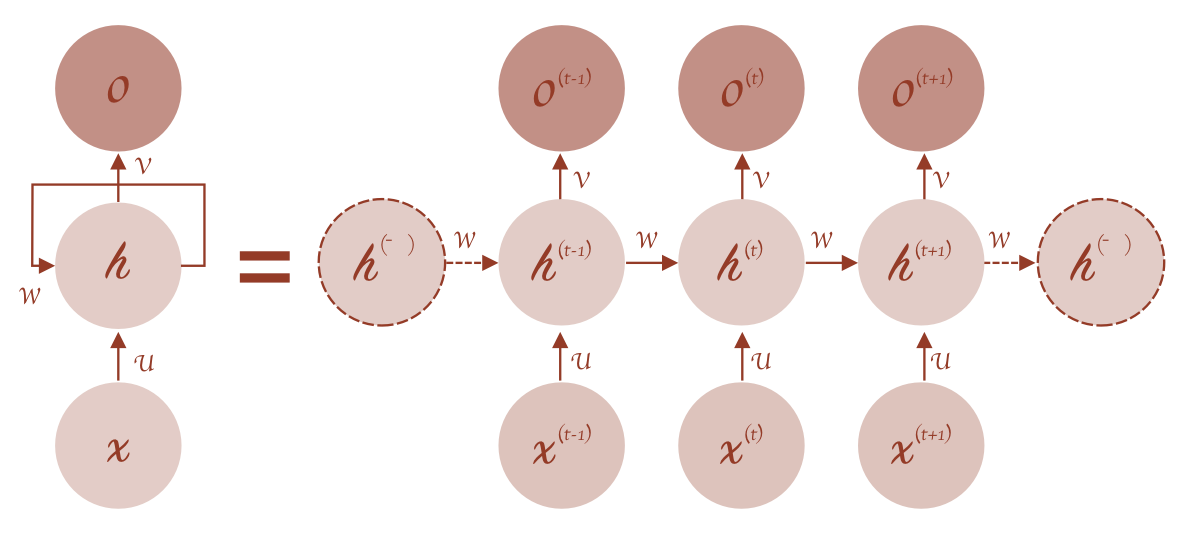
之前，我们将神经网络建模为:

$$\begin{array}{r}{y}_t=\sigma (W{x}_t+b)\\ y_{t+1}=\sigma (W{x}_{t+1}+b)\end{array}$$

现在我们将其更新为两两种方法，一个是Elman network:

$$\begin{array}{rl}{h}_t& ={\sigma }_h(W_h{x}_t+U_h{h}_{t?1}+b_h)\\ y_t& ={\sigma }_y(W_y{h}_t+b_y)\end{array}$$

还有一个是Jordan networks:

$$\begin{array}{rl}{h}_t& ={\sigma }_h(W_h{x}_t+U_h{y}_{t?1}+b_h)\\ y_t& ={\sigma }_y(W_y{h}_t+b_y)\end{array}$$

我们看一下区别，其实就是为了加上非线性变化。给h加了一个非线性变化，再给y加了一个非线性变化。

这两个人都是很著名的计算机科学家，他们提出来的模型有区别，一个是一直在传递这个h，一个是一直在传递y。但是都实现了yt时刻和xt有关，也和x_{t-1}有关。这两个都实现了这样的一种功能，只不过它们中间一直传递的东西不太一样。

这个就是RNN的内核，它的内核就是这个东西。

我们接着，就来看一个案例，这个案例中的数据是一个盈利数据, 还是老样子，数据集我就放在文末了。

我们这里是一个两个月每天的盈利指数，其中2点几的是盈利比较多，1点几的就是盈利比较少的。

timeserise_revenue = pd.read_csv('~/mount/Sync/data/AI_Cheats/time_serise_revenue.csv')
sales_data = pd.read_csv('~/mount/Sync/data/AI_Cheats/time_serise_sale.csv')

timeserise_revenue.drop(axis=1, columns='Unnamed: 0', inplace=True)
sales_data.drop(axis=1, columns='Unnamed: 0', inplace=True)

数据上我就不展示了，大家自己拿到后查看一下。我们现在要做的是，是想根据它前十天的一个数据，来预测一下第11天的数据。

很简单的方法咱们可以写一个全连接的网络：

class FullyConnected(nn.Module):
    def __init__(self, x_size, hidden_size, output_size):
        super(FullyConnected, self).__init__()
        self.hidden_size = hidden_size

        self.linear_with_tanh = nn.Sequential(
            nn.Linear(10, self.hidden_size),
            nn.Tanh(),
            nn.Linear(self.hidden_size, self.hidden_size),
            nn.Tanh(),
            nn.Linear(self.hidden_size, output_size)
        )
        
    def forward(self, x):
        yhat = self.linear_with_tanh(x)
        
        return yhat

我们输入10个值对它进行线性变化，再给它进行一个非线性变化，然后重复一遍，最后再来一次线性变化，这样就是最简单的一种线性和非线性变化的网络。

然后我们处理一下数据，设置一下相关参数：

sales_data.drop(axis=1, columns='Unnamed: 0', inplace=True)
source_data = sales_data

n_epochs = 30
hidden_size = 2 # try to change this parameters 
n_layers = 1
batch_size = 5
seq_length = 10
n_sample_size = 50

x_size = 1

fc_model = FullyConnected(x_size, hidden_size, output_size=seq_length)
fc_model = fc_model.double()

criterion = nn.MSELoss()
optimizer = optim.SGD(fc_model.parameters(), lr=0.01)

fc_losses = np.zeros(n_epochs) 

plt.imshow(fc_model.state_dict()['linear_with_tanh.0.weight'])

显示了一下一开始的权重。

之后我们来看一下整个的训练过程：

data_loader = torch.utils.data.DataLoader(source_data.values, batch_size=seq_length, shuffle=True)

for epoch in range(n_epochs):
    epoch_losses = []
    for iter_, t in enumerate(data_loader):
        random_index = random.randint(0, t.shape[-1] - seq_length - 1)
        train_x = t[:, random_index: random_index+seq_length]
        train_y = t[:, random_index + 1: random_index + seq_length + 1]

        outputs = fc_model(train_x.double())

        optimizer.zero_grad()
        loss = criterion(outputs, train_y)
        loss.backward()
        optimizer.step()

        epoch_losses.append(loss.detach())
    fc_losses[epoch] = np.mean(epoch_losses)

传入的data_loader是每一次随机的取期望的10个数字,这个数字我们就会根据序列来取出x和y, 然后把x送到模型里边得到outputs,得到outputs之后又出现熟悉的面孔, 我们求它的loss，再通过它的loss做反向传播。

optimizer做step，就是做全程的更新。

之后我们可以将每次循环的结果打印出来看看：

for epoch in range(n_epochs):
    ...
    for iter_, t in enumerate(data_loader):
        ...
        if iter_  == 0:
            plt.clf()
            plt.ion()
            plt.title("Epoch {}, iter {}".format(epoch, iter_))
            plt.plot(torch.flatten(outputs.detach()),'r-',linewidth=1,label='Output')
            plt.plot(torch.flatten(train_y),'c-',linewidth=1,label='Label')
            plt.plot(torch.flatten(train_x),'g-',linewidth=1,label='Input')
            plt.draw()
            plt.pause(0.05)

我们就不全展示了，大家可以自行去运行一下。

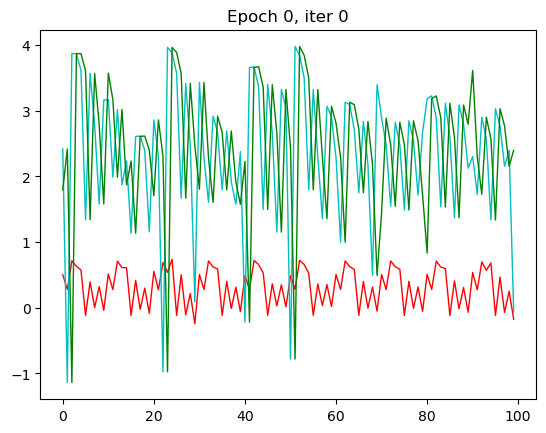
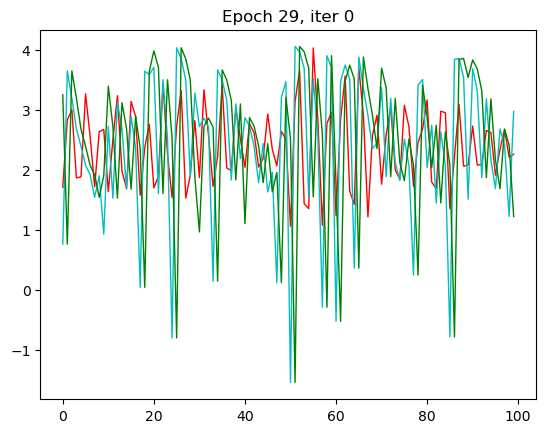
红色是预测值，绿色是输入值，蓝色是实际值。这里我只放了第一张和第30张，也就是本次循环的最后一张。

那一开始，预测出来值没有和我们实际的值相符，到了30的相较而言是比较相符了。

我们看看它的loss是否如预期的下降了：

plt.plot(fc_losses)

看完全连接的模型，再来看看RNN的模型，做一个非常简单的RNN模型，那首先还是定义模型：

class SimpleRNN(nn.Module):
    def __init__(self, x_size, hidden_size, n_layers, batch_size, output_size):
        super(SimpleRNN, self).__init__()
        self.hidden_size = hidden_size
        self.n_layers = n_layers
        self.batch_size = batch_size
        self.rnn = nn.RNN(x_size, hidden_size, n_layers, batch_first=True)
        self.out = nn.Linear(hidden_size, output_size) # 10 in and 10 out

    def forward(self, inputs, hidden=None):
        hidden = self.__init__hidden()
        output, hidden = self.rnn(inputs.float(), hidden.float())
        output = self.out(output.float());

        return output, hidden

    def __init__hidden(self):
        hidden = torch.zeros(self.n_layers, self.batch_size, self.hidden_size, dtype=torch.float64)
        return hidden

我们输入的是x_size，然后然后定义一个hidden_size。这里注意啊，hidden_size是可以改的，越大可以表示的中间层的信息就越多，但意味着需要更多的数据去训练它。

然后在forward里，可以看到每一步会输出一个output，到最后一步的时候我们把output做一个线性变化，就可以变成期望的这个结果。

那这个RNN模型其实非常的简单，就是进了一个RNN，然后做了一个线性变化，把output做成线性变化。

然后我们来看看具体表现如何， 那首先一样的是定义参数，数据可以用上一次整理过的数据，不需要再做一次了：

n_epochs = 30
hidden_size = 2 # try to change this parameters 
n_layers = 1
batch_size = 5
seq_length = 10
n_sample_size = 50

x_size = 1
output_size = 1

hidden = None

rnn_model = SimpleRNN(x_size, hidden_size, n_layers, seq_length, output_size)

criterion = nn.MSELoss()
optimizer = optim.SGD(rnn_model.parameters(), lr=0.01)

rnn_losses = np.zeros(n_epochs) 

然后我们就可以来跑一下了。

data_loader = torch.utils.data.DataLoader(source_data.values, batch_size=seq_length, shuffle=True)

for epoch in range(n_epochs):
    for iter_, t in enumerate(data_loader):
        if t.shape[0] != seq_length: continue 

        random_index = random.randint(0, t.shape[-1] - seq_length - 1)
        train_x = t[:, random_index: random_index+seq_length]
        train_y = t[:, random_index + 1: random_index + seq_length + 1]

        outputs, hidden = rnn_model(train_x.double().unsqueeze(2), hidden)

        optimizer.zero_grad()
        loss = criterion(outputs.double(), train_y.double().unsqueeze(2))
        loss.backward()
        optimizer.step()

        epoch_losses.append(loss.detach())
    rnn_losses[epoch] = np.mean(epoch_losses)

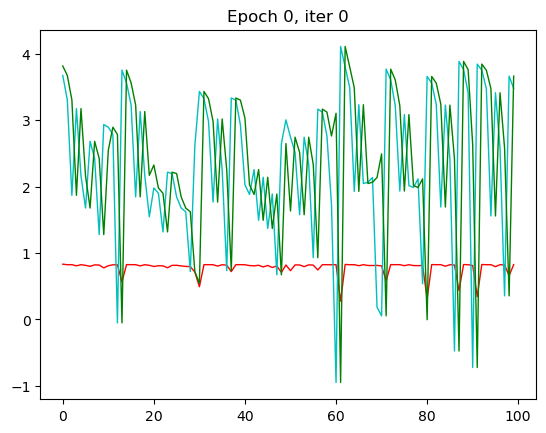
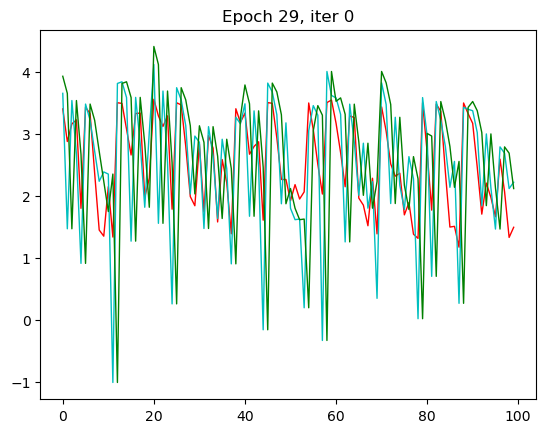
那RNN模型其实从第三轮的时候效果就已经出现了，我们的x一样，改变了一个模型之后拟合的效果就不一样了。

我们来看看它的loss：

RNN模型跑下来，loss是下降到了0.67左右，那我们之前的全连接模型的loss是在0.8以上，还是有一些区别的。我们可以将两个模型的loss打印到一张图上，就更能看出来两个模型的区别了。

plt.plot(rnn_losses, c='red')
plt.plot(fc_losses, c='green')

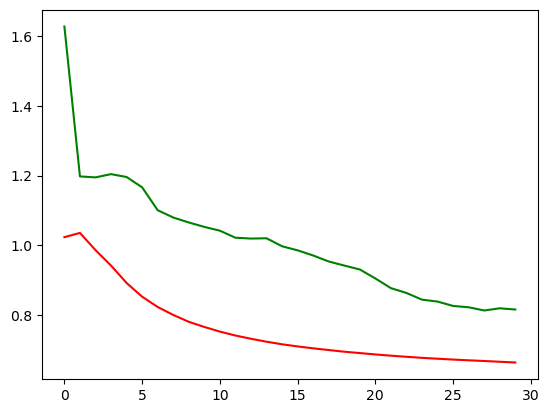
就可以看到，非常明显。

举这个例子作用是想说明，wx+b加上非线性变化这种形式其实也能解决问题，但是遇到时间相关，序列相关的问题的时候，解决效果就没有RN模型这么好。

为什么没有RNN模型好呢？因为RNN模型在这个过程中每一步把前一步的hidden的影响给它保留了下来。就是说它每一步的输出的时候不是单纯的考虑这一步的输出，把之前每一步的x的值其实都保留下来了。这个区别就是为什么要有RNN，以及大家之后什么时候用RNN。

因为我这边只是做个测试，所以仅仅做了30次epoch，那之后，大家可以尝试一下将epoch改成200或者更多，来看看具体loss会下降到什么程度。

好，文章最后，就是本文所用的数据集了：

time_serise_revenue.csv

链接: https://pan.baidu.com/s/1dL9XdBgoi3nC2VOC6w_wnw?pwd=qmw6 提取码: qmw6
–来自百度网盘超级会员v6的分享

time_serise_sale.csv

链接: https://pan.baidu.com/s/12wMJHzSZk91YPFcaG-K6Eg?pwd=1kmp 提取码: 1kmp
–来自百度网盘超级会员v6的分享