计算机速成课Crash Course - 13. 算法入门
今天继续计算机速成课Crash Course的系列讲解。
更多技术文章,全网首发公众号 “摸鱼IT” 锁定 -上午11点 - ,感谢大家关注、转发、点赞!
13. 算法入门
前两集,我们"初尝"了高级编程语言(比如 Python 和 Java),我们讨论了几种语句 - 赋值语句,if 语句,循环语句,以及把代码打包成 "函数",比如算指数。
重要的是,之前写的指数函数,只是无数解决方案的一种,还有其它方案,用不同顺序写不同语句,也能得到一样结果。
不同的是 "算法",意思是:解决问题的具体步骤,即使结果一致,有些算法会更好。
一般来说,所需步骤越少越好,不过有时我们也会关心其他因素,比如占多少内存。
"算法" 一词来自 波斯博识者 阿尔·花拉子密,1000 多年前的代数之父之一,如何想出高效算法 - 是早在计算机出现前就有的问题。

诞生了专门研究计算的领域,然后发展成一门现代学科,计算机科学!
记载最多的算法之一是"排序",比如给名字、数字排序,排序到处都是。找最便宜的机票,按最新时间排邮件,按姓氏排联系人,这些都要排序。
你可能想"排序看起来不怎么难… 能有几种算法呢?"答案是超多,计算机科学家花了数十年发明各种排序算法,还起了酷酷的名字,"冒泡排序""意面排序",我们来试试排序!
试想有一堆机票价格,都飞往印第安纳波利斯 (美国地名),数据具体怎么在内存中表示下周再说。
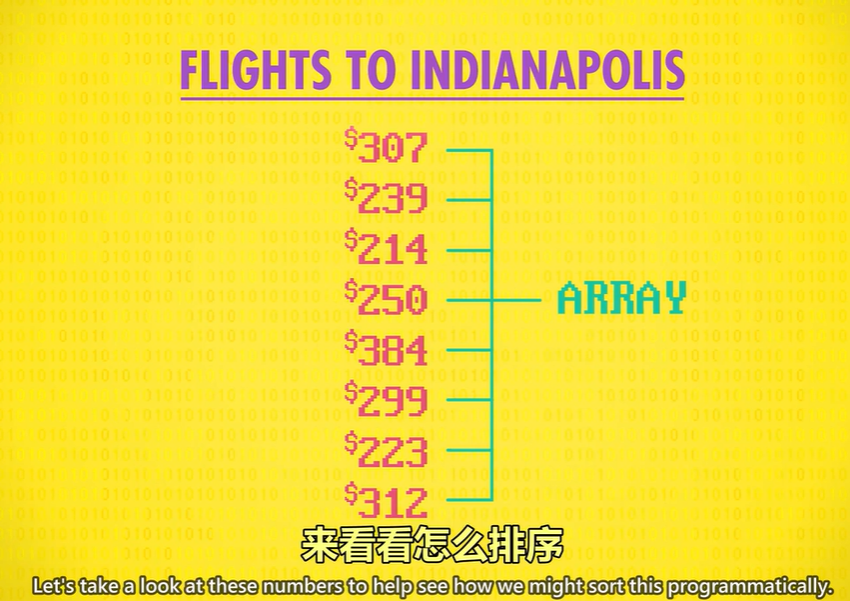
上图的这样一组数据? 叫"数组"(Array)来看看怎么排序,先从一种简单算法开始。
先找到最小数,从最上面的 307 开始,因为现在只看了这一个,所以它是最小数,下一个是 239,比 307 小,所以新的最小数变成 239,下一个是 214 ,新的最小数,250 不是,384, 299, 223, 312 都不是,现在扫完了所有数字。

214 是最小的,为了升序排列(从小到大排序),把 214 和最上面的数字,交换位置。刚排序了一个数字!

现在重复同样的过程,这次不从最上面开始,从第 2 个数开始,先看到 239,我们当作是 "最小数",扫描剩下的部分,发现 223 最小。
所以把它和第 2 位交换,重复这个过程,从第 3 位数字开始,让 239 和 307 互换位置,重复直到最后一个数字。
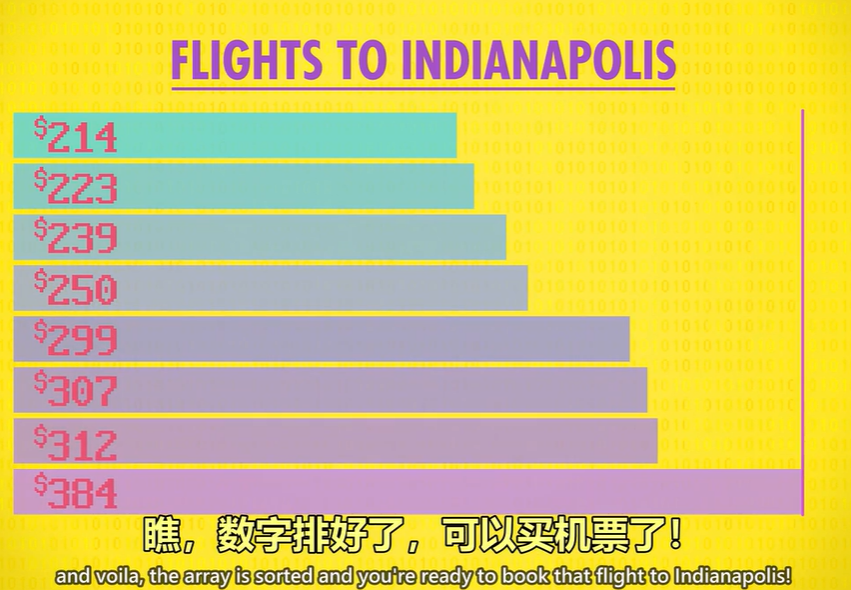
瞧,数字排好了,可以买机票了!
刚刚这种方法,或者说算法,叫 选择排序 - 非常基础的一种算法,以下是"伪代码"。
这个函数可以排序8个, 80个或8千万个数字,函数写好了就可以重复使用,这里用循环,遍历数组,每个数组位置都跑一遍循环,找最小数然后互换位置,可以在代码中看到这一点(一个 for 循环套另一个 for 循环)。

这意味着,大致来说,如果要排 N 个东西,要循环 N 次,每次循环中再循环 N 次,共 N*N, ?或 N平方。
算法的输入大小和运行步骤之间的关系,叫算法的“复杂度”,表示运行速度的量级,计算机科学家们把算法复杂度叫 -?大 O 表示法。
算法复杂度 O(N) 效率不高,前面的例子有 8 个元素(n=8), 8*8= 64,如果 8 个变 80 个,运行时间变成6400,虽然大小只增长了 10 倍(8 到 80),但运行时间增加了 100 倍!(64 到 6400 )
随着数组增大,对效率的影响会越来越大,这对大公司来说是个问题,比如谷歌,要对几十亿条信息排序。
作为未来的计算机科学家你可能会问:有没有更高效的排序算法?
回到未排序的数组,试另一个算法 "归并排序"。
第一件事是检查数组大小是否 > 1,如果是,就把数组分成两半,因为数组大小是 8,所以分成两个数组,大小是 4,但依然大于 1,所以再分成大小是 2 的数组,最后变成 8 个数组,每个大小为 1。

现在可以"归并"了,"归并排序"因此得名。
从前两个数组开始,读第一个(也是唯一一个)值307 和 239,239 更小,所以放前面,剩下的唯一数字是 307 ,所以放第二位,成功合并了两个数组,重复这个过程,按序排列,然后再归并一次。

同样,取前两个数组,比较第一个数,239 和 214,214 更小,放前面。再看两个数组里的第一个数:239 和 250,239 更小,所以放下一位。看剩下两个数:307 和 250,250 更小,所以放下一位。

最后剩下 307 ,所以放最后。
每次都以 2 个数组开始,然后合并成更大的有序数组,我们把刚隐藏起来的,下面的数组也这样做,现在有两个大小是 4 的有序数组,就像之前,比较两个数组的第一个数,取最小数,重复这个过程,直到完成。

就排好了!
总之,"归并排序"的算法复杂度是 O(n * log n),n 是需要 比较+合并 的次数和数组大小成正比,log N 是合并步骤的次数。
例子中把大小是 8 的数组,分成四个数组,然后分成 2 个,最后分成 1 个,分了 3 次。
重复切成两半,和数量成对数关系。
Log2 8=3 ,如果数组大小变成 16 - 之前的两倍,也只要多分割 1 次,因为 Log2 16=4,即使扩大一千倍,从8到8000,分割次数也不会增大多少log2 8000≈13,13 比 3 只是4倍多一点。
然而排序的元素多得多,因此"归并排序"比"选择排序"更有效率!
有好几十种排序算法,但没时间讲。
所以我们来谈一个经典算法问题:图搜索。
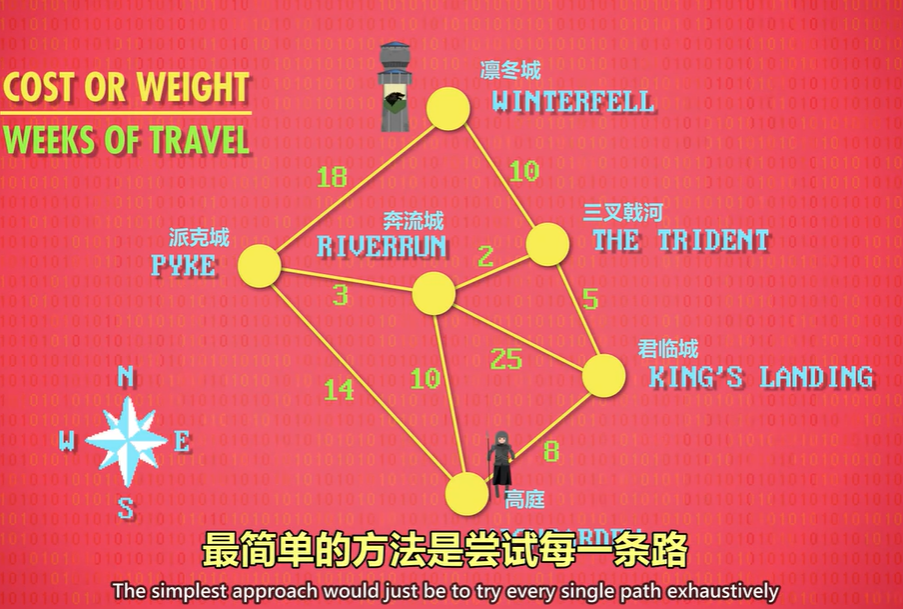
"图" 是用线连起来的一堆 "节点",可以想成地图,每个节点是一个城市,线是公路,一个城市到另一个城市,花的时间不同,可以用 成本(cost) 或 权重(weight) 来代称。
代表要几个星期。假设想找"高庭"到"凛冬城"的最快路线,最简单的方法是尝试每一条路,计算总成本,这是蛮力方法。
假设用蛮力方法来排序数组,尝试每一种组合,看是否排好序,这样的时间复杂度是 O(n!)
n 是节点数,n! 是 n 乘 n-1 乘 n-2... 一直到 1,比 O(n ?) 还糟糕!我们可以更聪明些!
图搜索问题的经典算法发明者是理论计算机科学的伟人 Edsger Dijkstra,所以叫 "Dijkstra 算法"。

从"高庭"开始,此时成本为0,把0标在节点里,其他城市标成问号,因为不知道成本多少,Dijkstra 算法总是从成本最低的节点开始。
目前只知道一个节点 "高庭", 所以从这里开始,跑到所有相邻节点,记录成本,完成了一轮算法,但还没到"凛冬城",所以再跑一次 Dijkstra 算法。
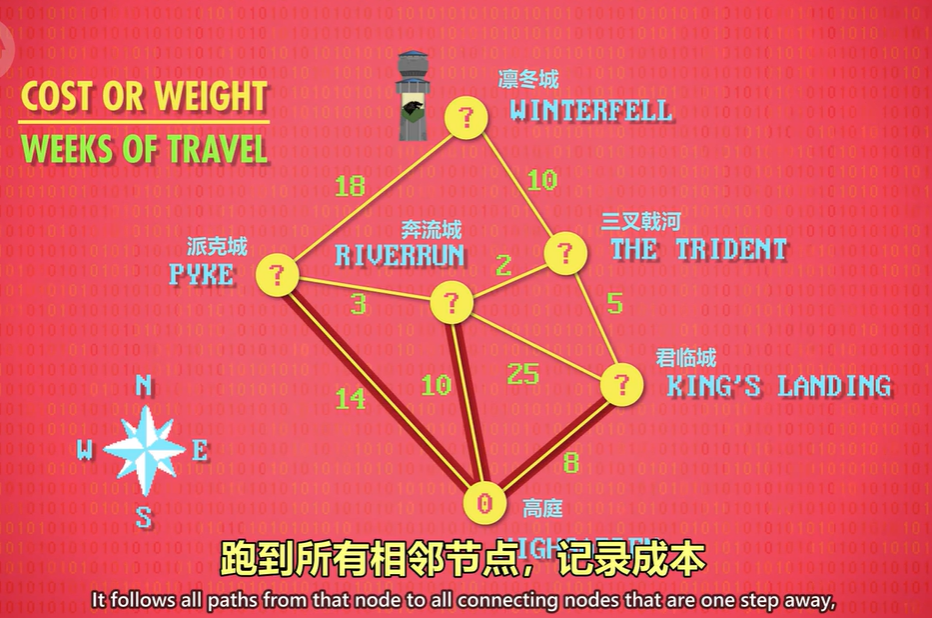
"高庭" 已经知道了,下一个成本最低的节点,是 "君临城",就像之前,记录所有相邻节点的成本,到"三叉戟河"的成本是 5。
然而我们想记录的是,从"高庭"到这里的成本,所以"三叉戟河"的总成本是 8+5=13周。
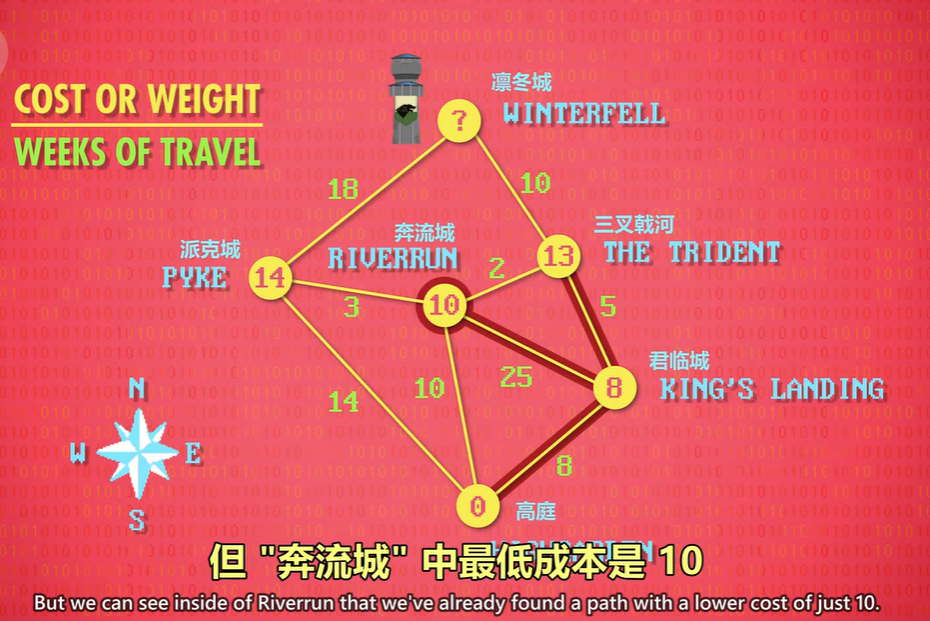
现在走另一条路到"奔流城",成本高达 25 ,总成本 33,但 "奔流城" 中最低成本是 10,所以无视新数字,保留之前的成本 10。
现在看了"君临城"的每一条路,还没到"凛冬城" 所以继续。
下一个成本最低的节点,是"奔流城",要 10 周,先看 "三叉戟河" 成本:10+2=12,比之前的 13 好一点,所以更新 "三叉戟河" 为 12。
"奔流城"到"派克城"成本是 3,10+3=13,之前是14,所以更新 "派克城" 为 13。
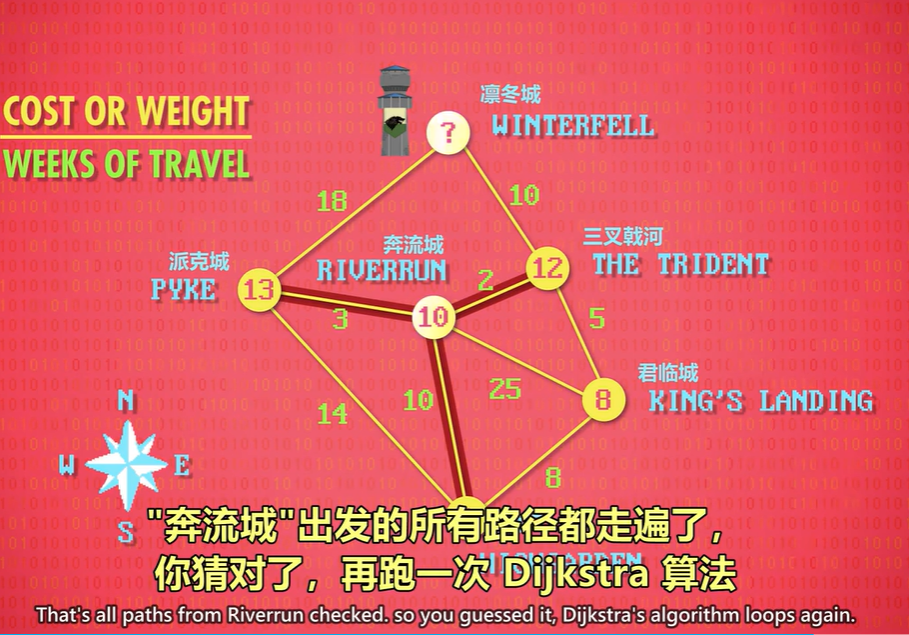
"奔流城"出发的所有路径都走遍了,你猜对了,再跑一次 Dijkstra 算法。
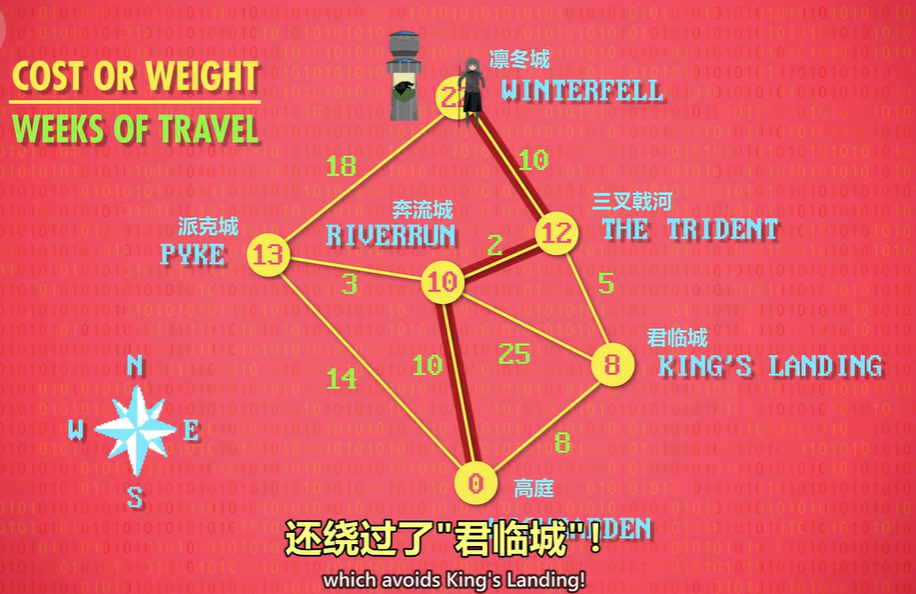
下一个成本最低的节点,是"三叉戟河",从"三叉戟河"出发,唯一没看过的路,通往"凛冬城",成本是 10,加"三叉戟河"的成本 12,总成本 22。
再看最后一条路,"派克城"到"凛冬城",成本 31,现在知道了最低成本路线,让军队最快到达,还绕过了"君临城"!
Dijkstra 算法的原始版本,构思于 1956 年,算法复杂度是 O(n),前面说过这个效率不够好,意味着输入不能很大,比如美国的完整路线图。
幸运的是,Dijkstra 算法几年后得到改进,变成 O(n log n + l),n 是节点数,l 是多少条线,虽然看起来更复杂,但实际更快一些。
用之前的例子,可以证明更快(6 个节点 9 条线),从 36 减少到 14 左右。

就像排序,图搜索算法也有很多,有不同优缺点。每次用谷歌地图时,类似 Dijkstra 的算法就在服务器上运行,找最佳路线。
算法无处不在,现代世界离不开它们,这集只触及了算法的冰山一角,但成为计算机科学家的核心。
是根据情况合理决定用现有算法还是自己写新算法,希望这集的小例子能让你体会到这点。
以上内容就是?13. 算法入门?的内容,感兴趣的同学记得点赞、关注、转发、收藏哦!
我会不定期发布课程的讲解!
更多技术文章,全网首发公众号 “摸鱼IT” 锁定 -上午11点 - ,感谢大家关注、转发、点赞!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!