GCN(图卷积)学习笔记
??CNN在图像上可以非常有效的提取特征,但是CNN处理的图像中像素点是排列成一个很整齐的矩阵,无法直接应用于图结构中,因为图中每个节点的邻接节点的数目可能都是不同的,那就无法用一个相同尺寸的卷积核进行卷积运算。但是我们又希望可以在图上有效的提取空间特征用于机器学习任务,于是GCN(图卷积网络)就被提出专用于提取图结构的空间特征,它主要分为空间域和谱域两个部分。
①基于空间的方法就是直接从图结构出发,聚合邻居节点的信息作为新的特征,不断的进行消息传递的过程。
②基于谱域的方法就是将原始数据转换至谱域中,利用图谱理论,引入滤波器进行滤波,在转换回时域的一个过程。
空间域的理解
??对于下面这张图G,有五个节点,它的邻接矩阵为A,特征矩阵为X。
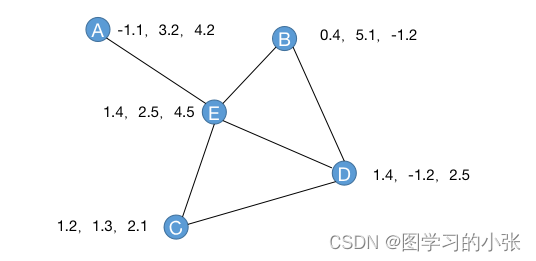
??根据GCN的思想,我们要聚合每个节点邻居节点的信息更新节点特征,就是将邻接矩阵与特征矩阵进行乘法操作:
X
(
1
)
=
A
×
X
X^{(1)}=A×X
X(1)=A×X
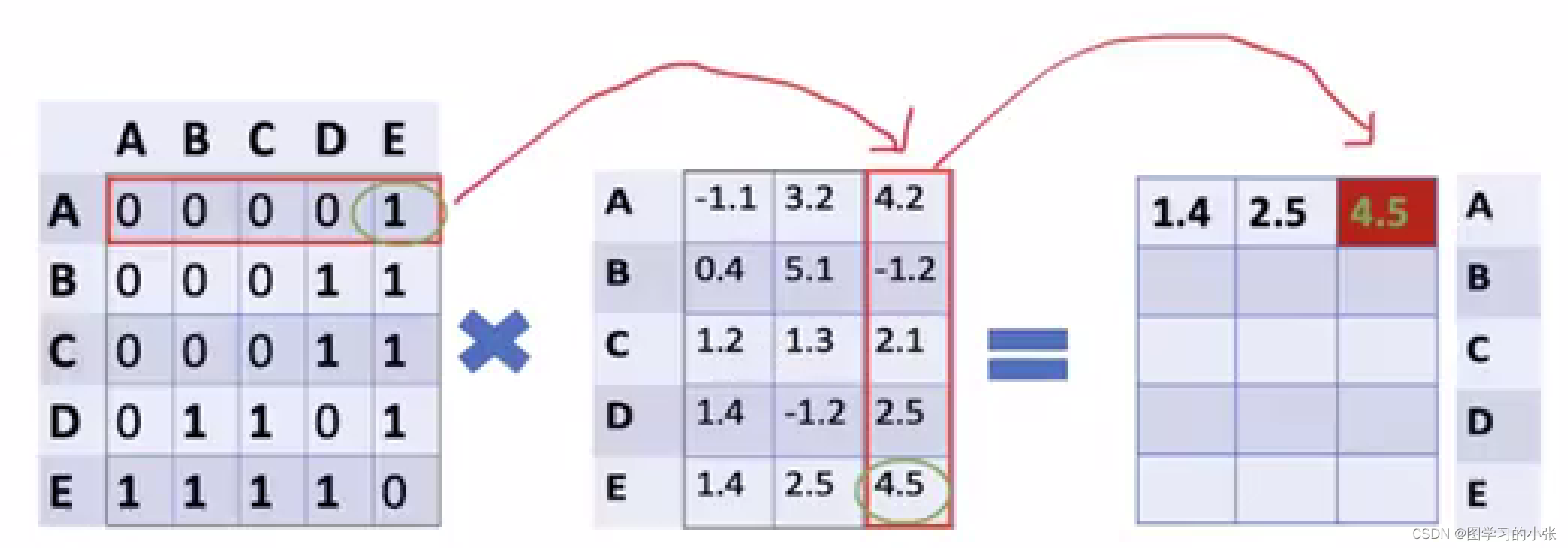
??这样进行一次计算后得到的特征矩阵就是所有邻居节点特征的加和,但是在邻接矩阵中没有自相连的边,在聚合特征的过程中把节点本身给忘掉了,所以要先给邻接矩阵A加一个对角阵:
A
~
=
A
+
I
\tilde{A}=A+I
A~=A+I ??这样就可以把所有的相关节点都考虑进去了,但是现在还有个问题:一个节点的度越大,它聚合的邻居节点的特征就会越多,它的特征值就会很大,于是我们引入
A
^
\hat A
A^的度矩阵:
??这样就可以把所有的相关节点都考虑进去了,但是现在还有个问题:一个节点的度越大,它聚合的邻居节点的特征就会越多,它的特征值就会很大,于是我们引入
A
^
\hat A
A^的度矩阵:
A
~
→
D
^
→
D
^
?
1
\tilde A\rightarrow \hat D\rightarrow \hat D^{-1}
A~→D^→D^?1
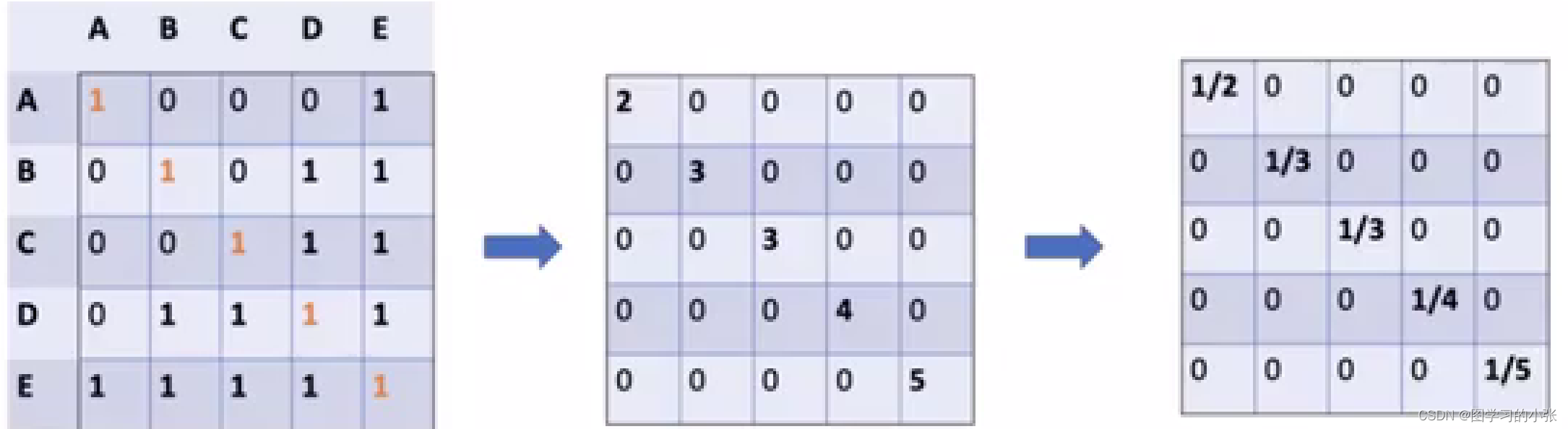
??根据矩阵乘法的性质,现在的公式就变成了:
D
^
?
1
(
A
~
X
)
=
(
D
^
?
1
A
~
)
X
\hat D^{-1}(\tilde AX)=(\hat D^{-1}\tilde A)X
D^?1(A~X)=(D^?1A~)X??相当于用度矩阵对邻接矩阵做了一个归一化,但是还没有结束,左乘一个度矩阵只对行做了归一化操作(上面那个
D
^
?
1
\hat D^{-1}
D^?1中的每个数会作用在更新后的特征矩阵的每一行,对每一行做平均),我们也需要对列做归一化操作,因为如果仅仅对行做归一化可能是不合理的,举个例子:

??有一个穷人(红框)只认识一个富人(绿框),那么穷人节点的特征与富人节点的特征进行平均后(对聚合特征后的特征矩阵行做归一化),我们的模型就会很容易认为他也是个富人,如果我们再对特征矩阵中的列做归一化,这样就会把富人节点的度也考虑进去(即邻居节点的度越大,权重就会越小),富人节点的度一般都是很多的,这样这个问题就解决了。
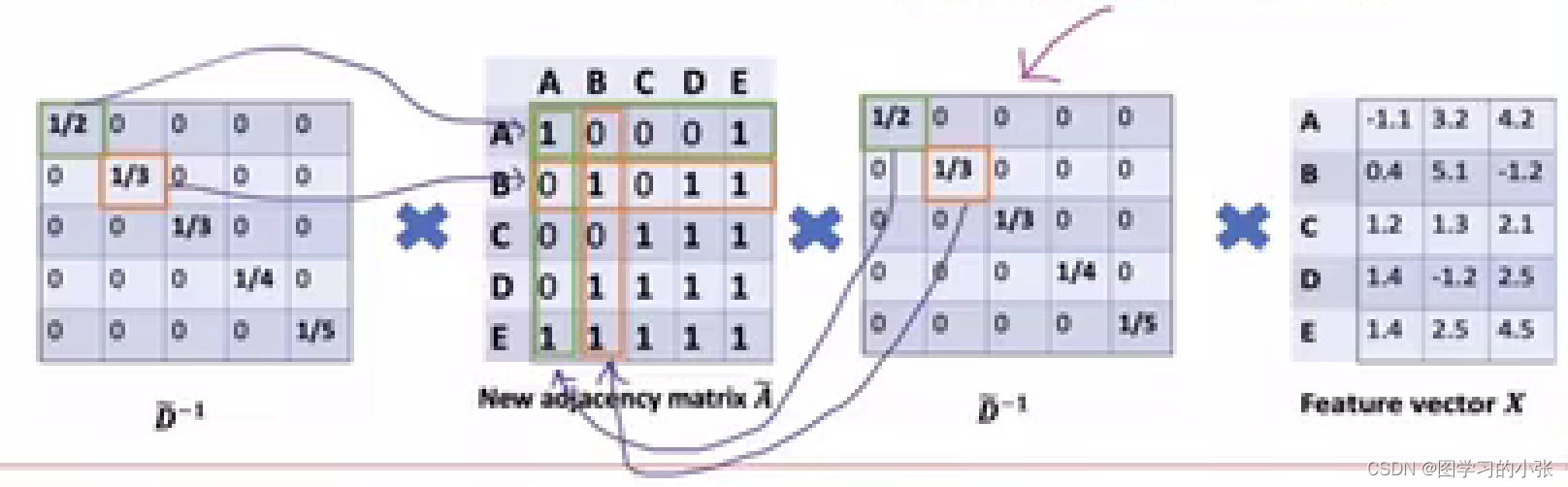
??但是左右都乘一个度矩阵后,相当于做了两遍归一化,那值就变得更小了,明显是不合理的,所以我们再对两边的度矩阵开个根号:
(
D
^
?
1
A
~
D
^
?
1
)
X
→
(
D
^
?
1
2
A
~
D
^
?
1
2
)
X
(\hat D^{-1}\tilde A\hat D^{-1})X\rightarrow(\hat D^{-\frac 12}\tilde A\hat D^{-\frac 12})X
(D^?1A~D^?1)X→(D^?21?A~D^?21?)X??于是我们就得到了一次GCN的过程:
X
l
+
1
=
D
^
?
1
2
A
~
D
^
?
1
2
X
l
X^{l+1}=\hat D^{-\frac 12}\tilde A\hat D^{-\frac 12}X^l
Xl+1=D^?21?A~D^?21?Xl??令:
A
^
=
D
^
?
1
2
A
~
D
^
?
1
2
\hat A =\hat D^{-\frac 12}\tilde A\hat D^{-\frac 12}
A^=D^?21?A~D^?21???有:
X
l
+
1
=
A
^
X
l
X^{l+1}=\hat AX^l
Xl+1=A^Xl??一个两层的GCN网络:
Z
=
A
^
σ
(
A
^
X
l
W
0
)
W
1
Z=\hat A\sigma(\hat AX^lW^0)W^1
Z=A^σ(A^XlW0)W1??其中,W是神经网络的权重,
A
^
X
l
\hat AX^l
A^Xl就是聚合了邻居信息的新的特征矩阵,
A
^
X
l
W
0
\hat AX^lW^0
A^XlW0就是进行了一次前向传播,经过激活函数
σ
\sigma
σ后又进行了一次前向传播。
频域的理解
??GCN是一种基于频域的方法,空间域的GCN只是频域GCN推导的一个特例,关于频域GCN,我直接推荐一个视频:图卷积神经网络(GCN)的数学原理详解——谱图理论和傅立叶变换,对图卷积的数学原理进行了详细的推导,过程挺复杂,有空再整理出来。
关于空间域的理解主要参考了:图神经网络GNN/GCN教程
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!