深入理解强化学习——马尔可夫决策过程：策略迭代-[基础知识]

分类目录：《深入理解强化学习》总目录

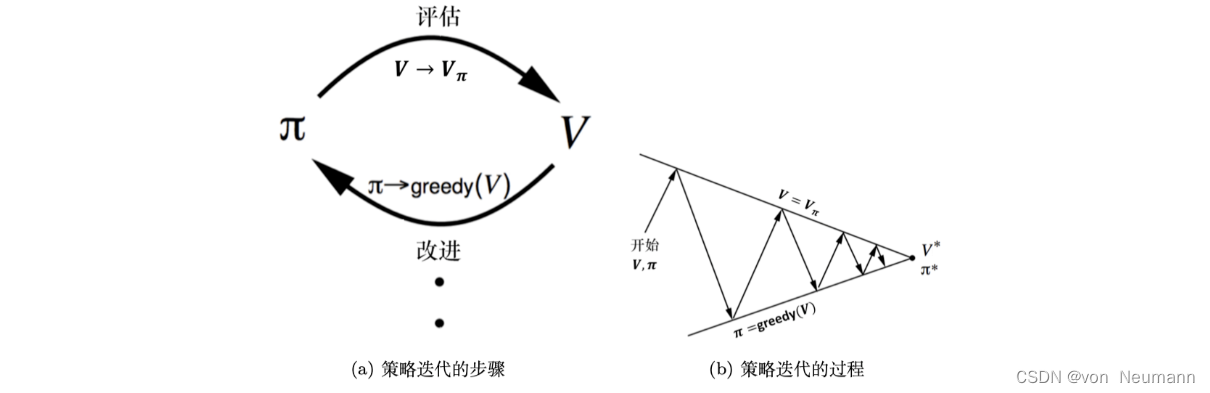
策略迭代由两个步骤组成：策略评估和策略改进（Policy Improvement）。如下图(a)所示，第一个步骤是策略评估，当前我们在优化策略$\pi$，在优化过程中得到一个最新的策略。我们先保证这个策略不变，然后估计它的价值，即给定当前的策略函数来估计状态价值函数。 第二个步骤是策略改进，得到状态价值函数后，我们可以进一步推算出它的Q函数。得到Q函数后，我们直接对Q函数进行最大化，通过在Q函数做一个贪心的搜索来进一步改进策略。这两个步骤一直在迭代进行。所以如下图(b)所示，在策略迭代里面，在初始化的时候，我们有一个初始化的状态价值函数$V$和策略$\pi$，然后在这两个步骤之间迭代。下图(b)上面的线就是我们当前状态价值函数的值，下面的线是策略的值。 策略迭代的过程与踢皮球一样。我们先给定当前已有的策略函数，计算它的状态价值函数。算出状态价值函数后，我们会得到一个Q函数。我们对Q函数采取贪心的策略，这样就像踢皮球，“踢”回策略。然后进一步改进策略，得到一个改进的策略后，它还不是最佳的策略，我们再进行策略评估，又会得到一个新的价值函数。基于这个新的价值函数再进行Q函数的最大化，这样逐渐迭代，状态价值函数和策略就会收敛。

这里再来看一下第二个步骤——策略改进，看我们是如何改进策略的。得到状态价值函数后，我们就可以通过奖励函数以及状态转移函数来计算Q函数：
$$Q_{{\pi }_i}(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}p(s^{\prime }|s,a)V_{{\pi }_i}(s^{\prime })$$

对于每个状态，策略改进会得到它的新一轮的策略，对于每个状态，我们取使它得到最大值的动作，即：
$${\pi }_{i+1}(s)=\arg \underset{a}{\max }{Q}_{{\pi }_i}(s,a)$$

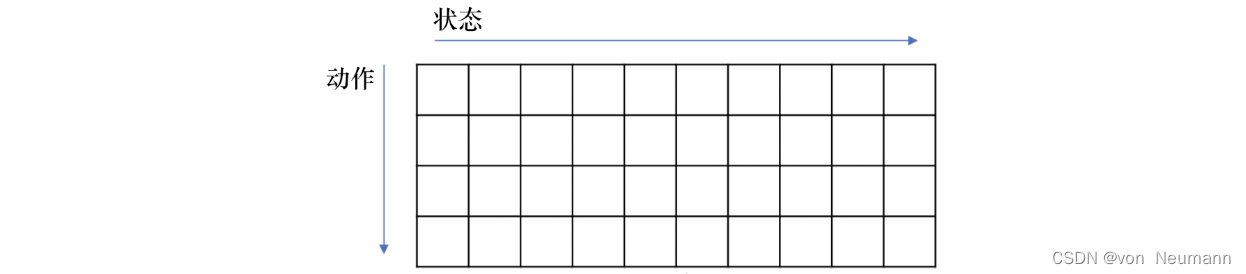
如下图所示，我们可以把Q函数看成一个Q表格（Q-table）：横轴是它的所有状态，纵轴是它的可能的动作。如果我们得到了Q函数，Q表格也就得到了。对于某个状态，每一列里面我们会取最大的值，最大值对应的动作就是它现在应该采取的动作。所以$\arg \max$操作是指在每个状态里面采取一个动作，这个动作是能使这一列的Q函数值最大化的动作。

参考文献：
[1] 张伟楠, 沈键, 俞勇. 动手学强化学习[M]. 人民邮电出版社, 2022.
[2] Richard S. Sutton, Andrew G. Barto. 强化学习（第2版）[M]. 电子工业出版社, 2019
[3] Maxim Lapan. 深度强化学习实践（原书第2版）[M]. 北京华章图文信息有限公司, 2021
[4] 王琦, 杨毅远, 江季. Easy RL：强化学习教程 [M]. 人民邮电出版社, 2022