Matlab通信仿真系列——多径衰落信道的建模和仿真

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录

一、多径衰落信道的特点
1、概念
2、Matlab仿真验证
二、多径衰落信道的建模和仿真
1、多径扩展
2、多普勒带宽
3、Jakes模型产生瑞利衰落信道
4、Rayleigh信道和awgn信道仿真
三、Matlab源码
1、多径衰落信道的特点的仿真源码
2、Rayleigh函数的仿真源码
3、Jakes模型的仿真源码
4、Rayleigh信道和awgn信道的仿真源码

本节内容
无线信道中，发送和接收天线之间通常存在多于一条的信号传播路径。
多径的存在是因为发射机和接收机之间建筑物和其他物体的反射、绕射、散射等引起的。当信号在无线信道传播时，多径反射和衰减的变化将使信号经历随机波动。无线信道的特性是不确定的，随机变化的。
一、多径衰落信道的特点
1、概念
多径衰落信道的两个特点：频率选择性衰落和时间选择性衰落。
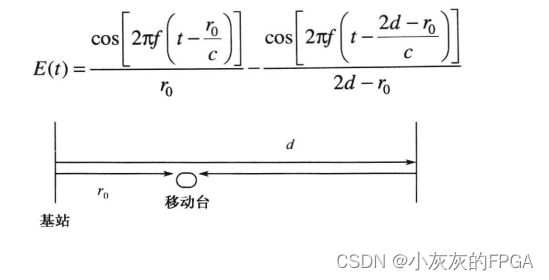
一个多径信道的模拟示例
在一条公路上一端安装固定的基站，另一端完全反射电磁波的墙面，基站到反射墙的距离为d。移动台到基站的初始距离为r0。基站发射一个频率为f的正弦信号，表示为cos(2πft)。移动台接收两路径信号，一路为基准发射的信号，另一路是反射墙反射过来的信号。
c—光速
r0/c—从基准发射信号到达移动台的时间
(2d-r0)/c—从反射墙反射过来的信号到达移动台的时间
E(t)—时刻t移动台接收到的合成信号

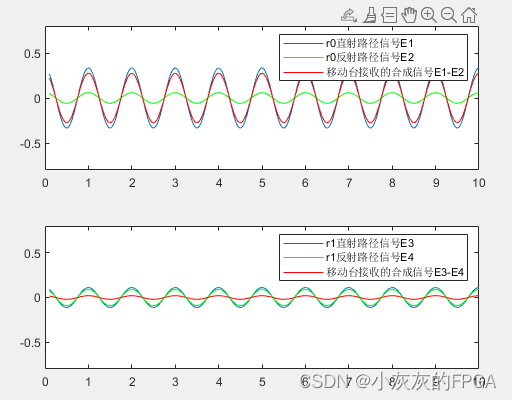
2、Matlab仿真验证

二、多径衰落信道的建模和仿真
多径衰落信道的建模和仿真，两个重要的参数是多径扩展和多普勒带宽。
1、多径扩展
若信道没有频率选择性，则最大的时延扩展Tmax要远远小于符合周期Ts,此时，所有的延迟路径分量到达的时段仅为一个符合时间的一小部分。
信道的单一路径建模，输入和输出关系为乘法，即

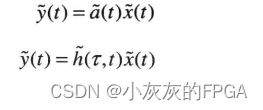
2、多普勒带宽
多普勒带宽又称为多普勒扩展，表示了信道特性作为时间的函数变化多快。多普勒频移与运动速度和方向相关，计算公式为

v—发送端和接收端的相对运动速度
θ—运动方向和发送端与接收端连线之间的夹角
3、Jakes模型产生瑞利衰落信道
多径衰落信道的仿真是产生特定多普勒功率谱密度的瑞利过程。
常用的多普勒功率谱密度是Jakes功率谱。

4、Rayleigh信道和awgn信道仿真

matlab代码示例：
对正交相移键控(QPDK)调制的基带数字通信，
系统通过AWGN信号的误符号率SER
和误比特率BER进行仿真验证，
发射端信息比特采用Gray编码，
基带脉冲采用矩阵脉冲，
仿真每个脉冲的抽样点数为10，
接收端采用匹配滤波器进行相干解调。
多普勒频移为100Hz，
经过矩阵脉冲成形后的信号
抽样时间间隔为1/(10×100000)s

三、Matlab源码
1、多径衰落信道的特点的仿真源码

clear all;
clc;
%发射信号的频率
f=1;
%移动台速度，静止情况下为0
v=0;
%光速
c=3e8;
%移动台到基站的初始距离r0
r0=3;
%移动台到基站的初始距离r1
r1=9;
%基站到反射墙的距离
d=10;
t=0.1:0.0001:10;
%r0直射路径信号
E1=cos(2*pi*f*((1-v/c).*t-r0/c))./(r0+v.*t);
%r0反射路径信号
E2=cos(2*pi*f*((1-v/c).*t-(r0-2*d)/c))./(2*d-r0-v*t);
%r1直射路径信号
E3=cos(2*pi*f*((1-v/c).*t-r1/c))./(r1+v.*t);
%r1反射路径信号
E4=cos(2*pi*f*((1-v/c).*t-(r1-2*d)/c))./(2*d-r1-v*t);
figure
subplot(2,1,1);
plot(t,E1,t,E2,'-g',t,E1-E2,'-r');
legend('r0直射路径信号E1','r0反射路径信号E2','移动台接收的合成信号E1-E2');
axis([0 10 -0.8 0.8]);



subplot(2,1,2);
plot(t,E3,t,E4,'-g',t,E3-E4,'-r');
legend('r1直射路径信号E3','r1反射路径信号E4','移动台接收的合成信号E3-E4');
axis([0 10 -0.8 0.8]);

2、Rayleigh函数的仿真源码

function [h] = rayleigh1(fd,t)
%改进的Jakes模型来产生单径的平坦型瑞利衰落信道
%输入变量说明
%   fd:信道的最大多普勒频移，单位Hz
%   t:信号的抽样时间序列
%   h:输出的瑞利信道函数，是一个时间函数复序列



    %入射波的数目
    N=40;
    
    wm=2*pi*fd;
    %每象限的入射波数目，即振荡器数目
    N0=N/4;
    %信道函数的实部
    Tc=zeros(1,length(t));
    %信道函数的虚部
    Ts=zeros(1,length(t));
    %归一化功率系数
    P_nor=sqrt(1/N0);
    %区别各条路径的均匀分布随机相位
    theta=2*pi*rand(1,1)-pi;
    for ii=1:N0
            %第i条入射波的入射角
            alfa(ii)=(2*pi*ii-pi+theta)/N;
               %对每个子载波在（-pi,pi）
              %之间的均匀分布的随机相位
            fi_tc=2*pi*rand(1,1)-pi;
            fi_ts=2*pi*rand(1,1)-pi;
            %计算冲激响应函数
            Tc=Tc+cos(cos(alfa(ii))*wm*t+fi_tc);
            Ts=Ts+cos(sin(alfa(ii))*wm*t+fi_ts);
    end
    %乘归一化功率系数输出传输函数
    h=P_nor*(Tc+j*Ts);
end

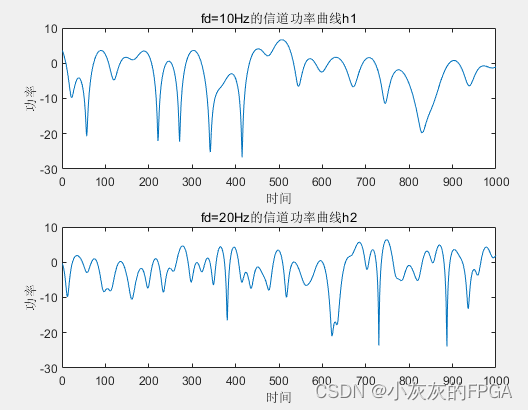
3、Jakes模型的仿真源码

clear all;
%clc;
%多普勒频移为10
fd=10;
t=0:0.001:1;
%产生信道数据h1
h1=rayleigh1(fd,t);
fd=20;
%产生信道数据h2
h2=rayleigh1(fd,t);


subplot(2,1,1);
plot(20*log10(abs(h1(1:1000))));
title('fd=10Hz的信道功率曲线h1');
xlabel('时间');
ylabel('功率');
subplot(2,1,2);
plot(20*log10(abs(h2(1:1000))));
title('fd=20Hz的信道功率曲线h2');
xlabel('时间');
ylabel('功率');

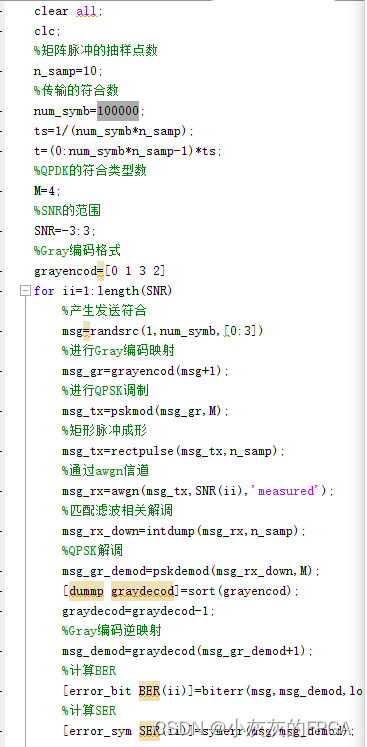
4、Rayleigh信道和awgn信道的仿真源码

clear all;
clc;
%矩阵脉冲的抽样点数
n_samp=10;    
%传输的符合数      
num_symb=100000;
ts=1/(num_symb*n_samp);
t=(0:num_symb*n_samp-1)*ts;
%QPDK的符合类型数  
M=4;   
%SNR的范围                 
SNR=-3:3;               
%Gray编码格式
grayencod=[0 1 3 2]     
for ii=1:length(SNR)
    %产生发送符合
    msg=randsrc(1,num_symb,[0:3])   
    %进行Gray编码映射
    msg_gr=grayencod(msg+1);        
    %进行QPSK调制
    msg_tx=pskmod(msg_gr,M);        
    %矩形脉冲成形
    msg_tx=rectpulse(msg_tx,n_samp);
    %通过awgn信道
    msg_rx=awgn(msg_tx,SNR(ii),'measured');
    %匹配滤波相关解调
    msg_rx_down=intdump(msg_rx,n_samp);
    %QPSK解调    
    msg_gr_demod=pskdemod(msg_rx_down,M);    
    [dummp graydecod]=sort(grayencod);            
    graydecod=graydecod-1;
    %Gray编码逆映射    
    msg_demod=graydecod(msg_gr_demod+1);
    %计算BER    
    [error_bit BER(ii)]=biterr(msg,msg_demod,log2(M));
    %计算SER
    [error_sym SER(ii)]=symerr(msg,msg_demod);
    %生成瑞利衰落
    h=rayleigh1(10,t);
    %信号通过瑞利衰落
    msg_tx1=h.*msg_tx;
     %通过awgn信道
    msg_rx1=awgn(msg_tx1,SNR(ii),'measured');    
    %匹配滤波相关解调
    msg_rx_down1=intdump(msg_rx1,n_samp);
    %QPSK解调    
    msg_gr_demod1=pskdemod(msg_rx_down1,M);    
    [dummp graydecod]=sort(grayencod);            
    graydecod=graydecod-1;
    %Gray编码逆映射    
    msg_demod1=graydecod(msg_gr_demod1+1);
    %计算BER    
    [error_bit1 BER1(ii)]=biterr(msg,msg_demod1,log2(M));
    %计算SER
    [error_sym1 SER1(ii)]=symerr(msg,msg_demod1);     
end


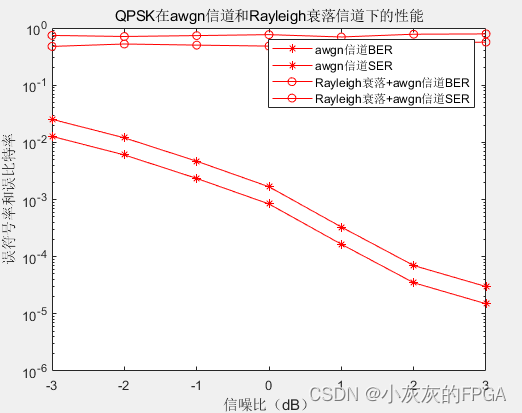
%画出BER和SER随SNR变换的曲线
semilogy(SNR,BER,'-r*',SNR,SER,'-r*',SNR,BER1,'-ro',SNR,SER1,'-ro')   
legend('awgn信道BER','awgn信道SER','Rayleigh衰落+awgn信道BER','Rayleigh衰落+awgn信道SER');
title('QPSK在awgn信道和Rayleigh衰落信道下的性能');
xlabel('信噪比（dB）');
ylabel('误符号率和误比特率');
axis([-3 3 10^(-6) 1]);