代码随想录算法训练营 | day46 动态规划 139.单词拆分，背包总结

刷题

139.单词拆分

题目链接 | 文章讲解 | 视频讲解

题目：给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。

你可以假设字典中没有重复的单词。

示例 1：

• 输入: s = "leetcode", wordDict = ["leet", "code"]

• 输出: true

• 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。

示例 2：

• 输入: s = "applepenapple", wordDict = ["apple", "pen"]

• 输出: true

• 解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。

• 注意你可以重复使用字典中的单词。

示例 3：

• 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]

• 输出: false

思路及实现

单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。

拆分时可以重复使用字典中的单词，说明就是一个完全背包！

动规五部曲分析如下：

1.确定dp数组以及下标的含义

dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。

2.确定递推公式

如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。

3.dp数组如何初始化

从递推公式中可以看出，dp[i] 的状态依靠 dp[j]是否为true，那么dp[0]就是递推的根基，dp[0]一定要为true，否则递推下去后面都都是false了。

那么dp[0]有没有意义呢？

dp[0]表示如果字符串为空的话，说明出现在字典里。

但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况，那么dp[0]初始为true完全就是为了推导公式。

下标非0的dp[i]初始化为false，只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。

4.确定遍历顺序

题目中说是拆分为一个或多个在字典中出现的单词，所以这是完全背包。

还要讨论两层for循环的前后顺序。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

而本题其实我们求的是排列数，为什么呢。 拿 s = "applepenapple", wordDict = ["apple", "pen"] 举例。

"apple", "pen" 是物品，那么我们要求 物品的组合一定是 "apple" + "pen" + "apple" 才能组成 "applepenapple"。

"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的，那么我们就是强调物品之间顺序。

所以说，本题一定是 先遍历 背包，再遍历物品。

5.举例推导dp[i]

以输入: s = "leetcode", wordDict = ["leet", "code"]为例，dp状态如图：

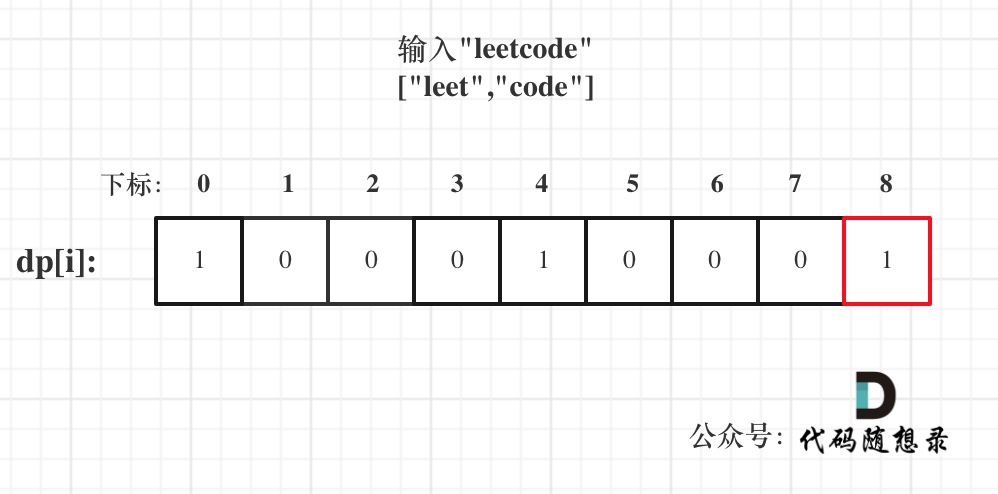
dp[s.size()]就是最终结果。

动规五部曲分析完毕，代码如下：

class Solution {
 ? ?public boolean wordBreak(String s, List<String> wordDict) {
 ? ? ? ?HashSet<String> set = new HashSet<>(wordDict);
 ? ? ? ?boolean[] valid = new boolean[s.length() + 1];
 ? ? ? ?valid[0] = true;
?
 ? ? ? ?for (int i = 1; i <= s.length(); i++) {
 ? ? ? ? ? ?for (int j = 0; j < i && !valid[i]; j++) {
 ? ? ? ? ? ? ? ?if (set.contains(s.substring(j, i)) && valid[j]) {
 ? ? ? ? ? ? ? ? ? ?valid[i] = true;
 ? ? ? ? ? ? ?  }
 ? ? ? ? ?  }
 ? ? ?  }
?
 ? ? ? ?return valid[s.length()];
 ?  }
}
?
// 另一种思路的背包算法
class Solution {
 ? ?public boolean wordBreak(String s, List<String> wordDict) {
 ? ? ? ?boolean[] dp = new boolean[s.length() + 1];
 ? ? ? ?dp[0] = true;
?
 ? ? ? ?for (int i = 1; i <= s.length(); i++) {
 ? ? ? ? ? ?for (String word : wordDict) {
 ? ? ? ? ? ? ? ?int len = word.length();
 ? ? ? ? ? ? ? ?if (i >= len && dp[i - len] && word.equals(s.substring(i - len, i))) {
 ? ? ? ? ? ? ? ? ? ?dp[i] = true;
 ? ? ? ? ? ? ? ? ? ?break;
 ? ? ? ? ? ? ?  }
 ? ? ? ? ?  }
 ? ? ?  }
?
 ? ? ? ?return dp[s.length()];
 ?  }
}
?
// 回溯法+记忆化
class Solution {
 ? ?private Set<String> set;
 ? ?private int[] memo;
 ? ?public boolean wordBreak(String s, List<String> wordDict) {
 ? ? ? ?memo = new int[s.length()];
 ? ? ? ?set = new HashSet<>(wordDict);
 ? ? ? ?return backtracking(s, 0);
 ?  }
?
 ? ?public boolean backtracking(String s, int startIndex) {
 ? ? ? ?// System.out.println(startIndex);
 ? ? ? ?if (startIndex == s.length()) {
 ? ? ? ? ? ?return true;
 ? ? ?  }
 ? ? ? ?if (memo[startIndex] == -1) {
 ? ? ? ? ? ?return false;
 ? ? ?  }
?
 ? ? ? ?for (int i = startIndex; i < s.length(); i++) {
 ? ? ? ? ? ?String sub = s.substring(startIndex, i + 1);
     ? ?// 拆分出来的单词无法匹配
 ? ? ? ? ? ?if (!set.contains(sub)) {
 ? ? ? ? ? ? ? ?continue; ? ? ? ? ? ? ? ?
 ? ? ? ? ?  }
 ? ? ? ? ? ?boolean res = backtracking(s, i + 1);
 ? ? ? ? ? ?if (res) return true;
 ? ? ?  }
 ? ? ? ?// 这里是关键，找遍了startIndex~s.length()也没能完全匹配，标记从startIndex开始不能找到
 ? ? ? ?memo[startIndex] = -1;
 ? ? ? ?return false;
 ?  }
}

背包总结

背包问题是动态规划里的非常重要的一部分，所以我把背包问题单独总结一下，等动态规划专题更新完之后，我们还会在整体总结一波动态规划。

关于这几种常见的背包，其关系如下：

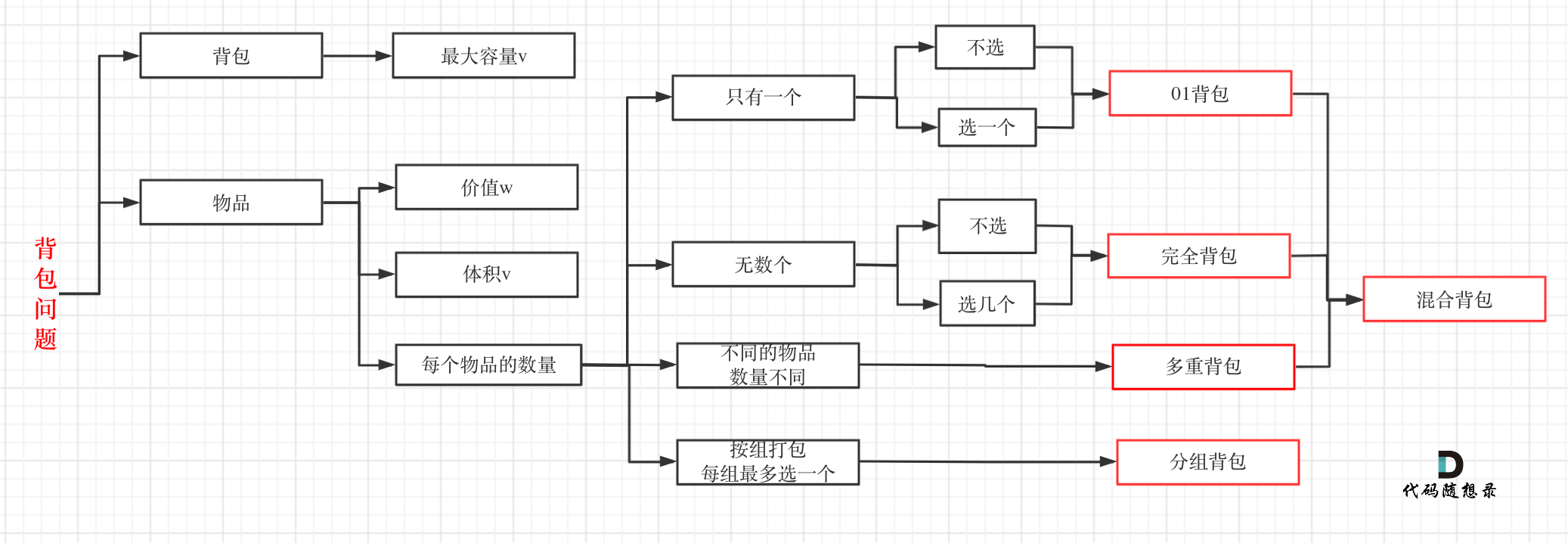
通过这个图，可以很清晰分清这几种常见背包之间的关系。

在讲解背包问题的时候，我们都是按照如下五部来逐步分析，相信大家也体会到，把这五部都搞透了，算是对动规来理解深入了。

1. 确定dp数组（dp table）以及下标的含义

2. 确定递推公式

3. dp数组如何初始化

4. 确定遍历顺序

5. 举例推导dp数组

其实这五部里哪一步都很关键，但确定递推公式和确定遍历顺序都具有规律性和代表性，所以下面我从这两点来对背包问题做一做总结。

背包递推公式

问能否能装满背包（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

• 动态规划：416.分割等和子集

• 动态规划：1049.最后一块石头的重量 II

问装满背包有几种方法：dp[j] += dp[j - nums[i]] ，对应题目如下：

• 动态规划：494.目标和

• 动态规划：518. 零钱兑换 II

• 动态规划：377.组合总和Ⅳ

• 动态规划：70. 爬楼梯进阶版（完全背包）

问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

• 动态规划：474.一和零

问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

• 动态规划：322.零钱兑换

• 动态规划：279.完全平方数

遍历顺序

01背包

二维dp数组01背包先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

一维dp数组01背包只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的，大家需要注意！

完全背包

说完01背包，再看看完全背包。

纯完全背包的一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

但是仅仅是纯完全背包的遍历顺序是这样的，题目稍有变化，两个for循环的先后顺序就不一样了。

如果求组合数就是外层for循环遍历物品，内层for遍历背包。

如果求排列数就是外层for遍历背包，内层for循环遍历物品。

相关题目如下：

• 求组合数：动态规划：518.零钱兑换II

• 求排列数：动态规划：377. 组合总和 Ⅳ?、动态规划：70. 爬楼梯进阶版（完全背包）

如果求最小数，那么两层for循环的先后顺序就无所谓了，相关题目如下：

• 求最小数：动态规划：322. 零钱兑换?、动态规划：279.完全平方数

对于背包问题，其实递推公式算是容易的，难是难在遍历顺序上，如果把遍历顺序搞透，才算是真正理解了。

总结

这篇背包问题总结篇是对背包问题的高度概括，讲最关键的两部：递推公式和遍历顺序，结合力扣上的题目全都抽象出来了。

而且每一个点，我都给出了对应的力扣题目。

最后如果你想了解多重背包，可以看这篇动态规划：关于多重背包，你该了解这些！，力扣上还没有多重背包的题目，也不是面试考察的重点。

如果把我本篇总结出来的内容都掌握的话，可以说对背包问题理解的就很深刻了，用来对付面试中的背包问题绰绰有余！

背包问题总结：

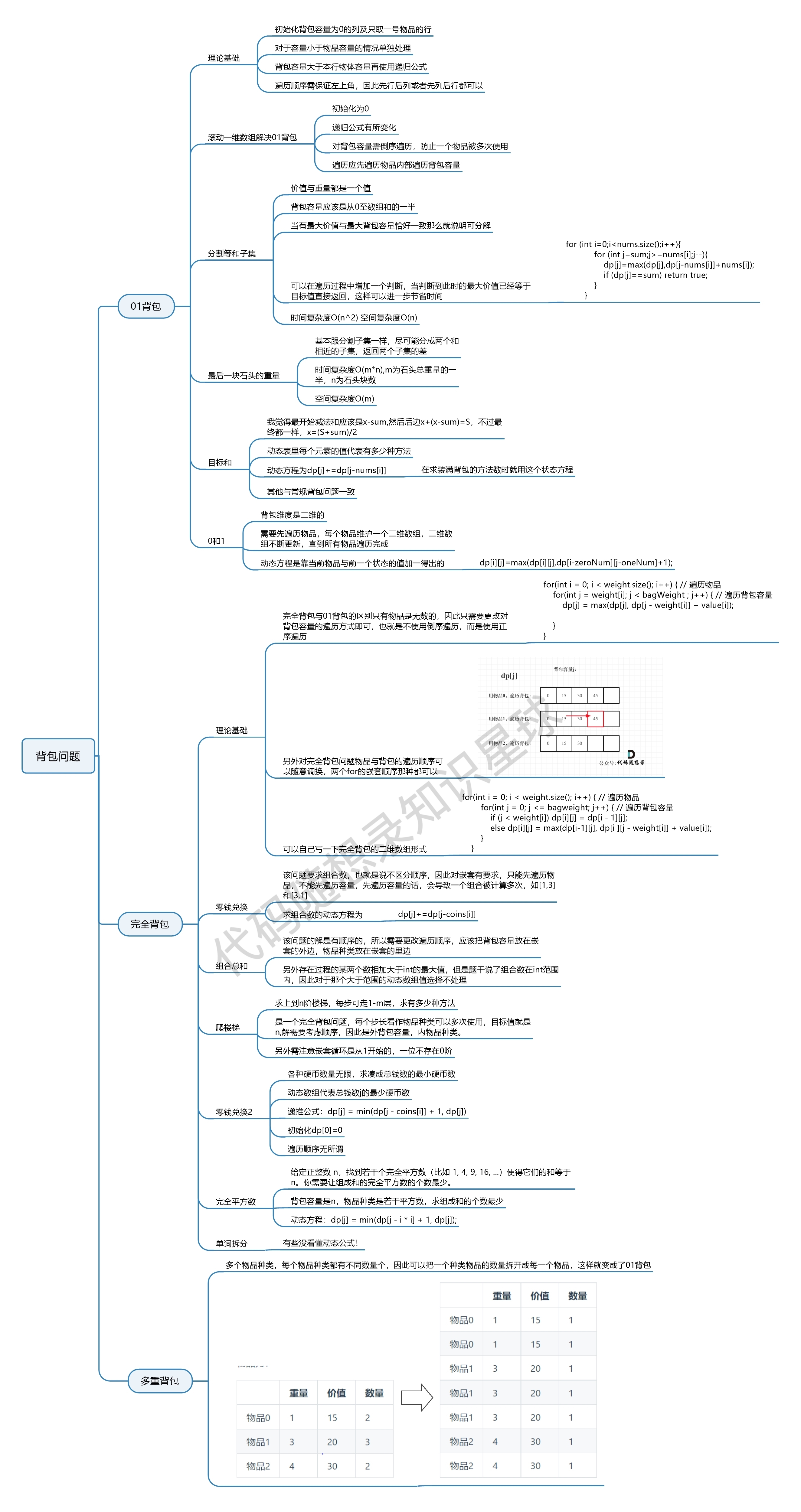
图源：海螺人