30. 深度学习进阶 - 池化

Hi,你好。我是茶桁。
上一节课,我们详细的学习了卷积的原理,在这个过程中给大家讲了一个比较重要的概念,叫做input channel,和output channel。
当然现在不需要直接去实现, 卷积的原理PyTorch、或者TensorFlow什么的其实都实现了。但我们现在如果要用PyTorch的卷积操作,它就会有一个input channel和output channel的一个写法。

这里的方法是Conv2d,表示这里所应用的filter是一个2d的。那么它如何去做3d的? 是将每一层的结果加在一起。
与此对应的还有一个Conv3d, 这个时候filter就是很多个不一样的。
我们一般在使用的时候,应用的都是Conv2d。感觉上好像觉得Conv3d里,我们每一层的值不一样其实会更好。但其实现在得到的这个filter是咱们人工写的,但是我们为了提取出来大自然中非常非常多的特征,其实我们会让机器自动生成、自动初始化一堆filter,这些filter的结果全部都是随机的。
就是说,这个filter的结果在深度学习中其实这些结果都是随机的,然后通过训练和反向传播,这些filter会自动地学习出来一个值。也就是说它会自动地收敛到某个数值上,而这个数值在这种环境下卷积应该怎么提取特征,那么我们做成2D的话所需要拟合的参数其实就少了。
假如filters前边的input channel很多、很深,那么这个filters需要拟合的参数也很多,如果是2D的话,只需要拟合2D的这一层就可以了。这就是2D和3D的区别,以及为什么一般要用2D不用3D。
如果现在要用卷积的话,第一个参数就是input channel。第二个就是output channel。output channel其实就是有多少个filters。
那kernel size指的就是做卷积的时候这个卷积的大小。比方说是3 * 3的,那么Kernel size就是3,也可以写成(3,3)。
还有一个参数叫做stride,这个stride就是步幅。那这个步幅是干什么的?我们一般用filter去卷积图像的时候,在矩阵上是一个单位一个单位从左到右从上到下移动的,这个步幅是为了加快移动,从而设置的间隔。比如[10, 9, 8, 7, 6], 那我就拿一行来举例,知道意思就行了。比如这样一个数列,如果filter是3列,那按顺序就应该先是[10, 9, 8],然后是[9, 8, 7], 但是我设置了stride就可以跳步来执行。在[10, 9, 8]之后,可以是[8, 7, 6]。stride默认为1。
下面一个参数, padding。假如是一个6 * 6的图像矩阵,有一个3 * 3的filter, 那么对这6 * 6的图像进行卷积,会先变成一个4 * 4,然后变成2 * 2。显示出来的结果就是在不断地变小,代表抽象层次越来越高。
那么因为每一次window都在不断变化,在进行下一轮的时候,如果这中间要加一些什么操作,维度发生变化,会导致每一次中间要连接什么东西的时候维度都得重新去计算。
也就说维度不断的变化,会导致写代码的时候计算会变得更复杂。
那第二,就是我们也不希望减少的太快了。举个极端情况,把1万 * 1万的图像很快就变成一个2 * 2的了。抽象层次太高信息就少了。
第三个解释起来比较复杂,我们脑子里想想一下,一个filter在图像上进行从左到右移动,那么在依次进行卷积计算的时候,最左边的一列就只计算了一次,但是中间位置就会被卷入计算多次。我们希望的是边上的的数据也能被计算多次,就是也能被反复的提取。
要解决这三个问题有一个很简单的方法,就是padding。它的意思就是在这个图形外边加了一圈或者两圈0。如果你要加一圈0的话,padding=1。如果等于2的话,就加两圈0。

接下来,dilation。这个是在我们做图形的分割的时候用的。在图形识别的时候大家现在先不用去学习它。
我们一张图片进行卷积的时候,会越来越小,这个叫做下采样, down sampling。进行完下采样之后,如果要做图像的切分,我们要把图像里边主体部分全部给它涂黑,别的地方全部涂白,需要基于这个小的采样又把它给扩大,慢慢恢复到原来大小,这个叫做上采样。上采样时,有时候会用到dilation。
重要的就是这几个参数。这几个参数给大家说完,其实基本上卷积的几个重要的特性就说明白了。
池化
除了卷积之外,还有一个比较重要的操作: pooling, 池化操作。
池化操作其实很简单,我们给定一个图片,卷积操作是选了一个window和filter,做了一个f乘w然后给它做相加. sum(f*w). pooling是一个很直接的操作, 把w这里边所有的值给它取个平均值, 也有可能取个最大值。假如是它最大值,那么值最大就代表着是在这个图形里边对他影响最重的这个点。
那么做了pooling之后,每一次这样一个操作,图形变小了,但是图像基本上保持了原来的样子。就是pooling操作前后的图像是相似的,它取了最重要的信息。
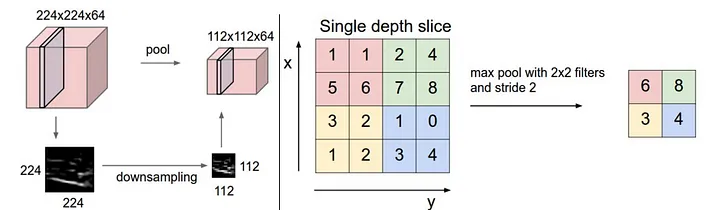
我们现在来思考一下,如果有一个图片,不管是卷积还是pooling都会让其缩小。那我们思考下, 既然两个操作都会导致图像缩小,那为什么会存在两个操作呢?
咱们机器学习里面最头疼的事情就是所谓的过拟合,过拟合就是在训练的时候效果挺好,结果在实际中效果就不好了。
而控制过拟合最主要的就是能够减少参数,在越少的参数能达到效果的时候,我们期望参数越少越好,在同样的数据量下就越能防止过拟合。
卷积里面这些值以前的时候是人来确定,但现在其实是期望机器自动的去求,也就是说这个参数是需要自己去求解的。而pooling并不需要去设定参数,它没有参数,这样会减少参数。
用了pooling之后不仅减少了参数, 还减少了接下来x的维度。所以最核心的其实是我们减少了所需要训练的参数。
之所以用pooling是因为可以减少参数,可以让它的过拟合的问题减弱。但是如果你的数据量本身就很多,或者说模型本身就比较好训练、好收敛,那你没有这个pooling操作其实也是可以的。
权值共享和位置平移
那么这个时候就要跟大家来讲一个比较重要的概念,叫做权值共享和局部不变性: Parameters Sharing and Location Invariant.这个Loction Invariant也有人把它叫做shifting Invariant。CNN的最重要的两个特点,第一个特点就是它的权值共享。
我们给定一个图片,就之前我那个头像,假如有一个filter,它是3 * 3的,那么这3 * 3的这个网格它在每一个窗口上都是和这个filter做的运算。
那么大家想一下,假如有一个1,000乘以1,000的一个图形,我们这1,000 * 1,000的图形我们要把它写成wx+b的话,这个x是100万维的,那么这个w也是100万维的。
那么如果我们要做训练的话,就要训练100万个w。这是拟合一个线性变化,那么我们如果现在是要去拟合一个卷积,假如output channel是10,那我们需要拟合的参数是多少?
卷积核是3 * 3, 有10个。 那就是9 * 9再乘以10。不管这个地方是1,000 * 1,000还是1万 * 1万,我们要拟合的都是卷积核里的这个参数。
我们做一层卷积,哪怕给了10个卷积核,也是九十个。如果要给它做一层线性变化,得100万个,这两个相差特别大。
为什么相差这么大?是因为不同的位置上用的filter的值是一样的。filter的参数整个图像共享了。这就是卷积神经网络的权值共享。
那么我们现在想一下,我们有了这个Parameters Sharing,它的作用是什么?
减少参数量的作用是防止过拟合,防止过拟合的最终体现就是我们在各种计算机视觉上的任务,表现就好。除此之外还有一个特性,它可以大大的提升我们的计算速度。
本来我们以前如果你有这么多参数的话,要反向传播一次要进行100万个反向传播。现在我们只要进行九十个就行了。
所以权值共享其实是卷积神经网络为什么效果特别好的原因。
2012年的时候,计算机视觉的测试效果一下子有了突飞猛进。当时就是因为用了卷积神经网络。
以前大家在实验室环境下,在训练集上的效果都挺不错,但是一拿到测试集的时候效果就很差。后来用卷积神经网络之后,这个错误率一下就下降了。
权值共享这个特性因此带来了一个特点,就是Loction Invariant。就是一个局部的东西,我们把它信息连接在一块了。
我们分别有两张图片,比如下面这张我以前画的一幅画,我把构图分别改变一下。

这两个图像数据表征上是很不一样,但是眼睛所在的位置经过卷积之后,只要用的是同一个卷积核,产生的结果是相似的。所以这个Loction Invariant指的意思是,不管这个眼睛在哪我们都能提取出来。
假设我们在train的时候, 眼睛不管在哪,只要把这个filter训练出来了,在test数据集上就算它的位置变了我们依然能够提取出来它的特征,依然能够计算出来和它相似的这个值,这个就叫做Loction Invariant。
这两个特性是极其重要的。
搭建卷积神经网络这个事,说实话最主要的还是要看经验。那么前人的总结就很值得借鉴,下节课,我们就来看看几种经典的神经网络结构。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!